№ 1.
 1. 1.
| 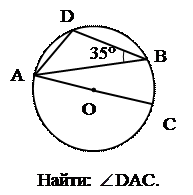 2. 2.
| 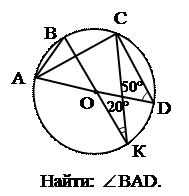 3. 3.
| ||||
 4. 4.
| 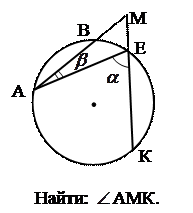 5. 5.
| 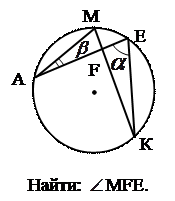 6. 6.
|
Рис. 69
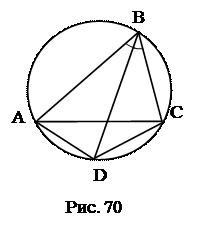
№2. Биссектриса угла В треугольника АВС пресекает описанную окружность в точке D. Доказать, что треугольник АDC равнобедренный.
 План доказательства.
План доказательства.
1. 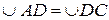 (доказать).
(доказать).
2. 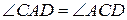 .
.
3. AD=CD.
Используемые факты из теоретической карты: 1.2.
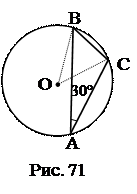
№3. Доказать, что сторона треугольника, лежащая против угла в 300, равна радиусу окружности, описанной около треугольника.
 План доказательства.
План доказательства.
1. 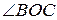 .
.
2. Вид 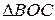 .
.
3. 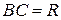
Используемые факты из теоретической карты:
1.1; 1.2.
№4. Угол при вершине равнобедренного треугольника равен 40°. Одна из
боковых сторон служит диаметром полуокружности, которая делится другими сторонами на три дуги. Найти градусные меры этих дуг.
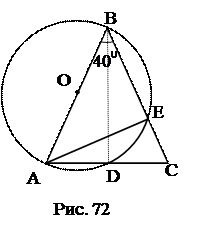 План решения.
План решения.
1. BD 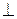 АС.
АС.
2. 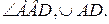
3. 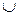
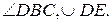
4. 
Ответ: 400, 400, 1000
Используемые факты из теоретической карты: 1.2.
№5. Через вершины Ви С треугольника АВС проходит окружность, пересекающая стороны АВ и АС в точках К и М соответственно. Доказать, что ∆АВС~ ∆АМК. Найти МК и АМ, если АВ=2, ВС=4, АС=5, АК=1.
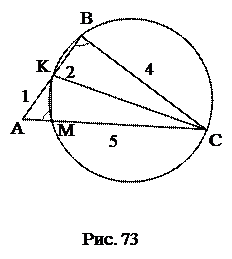 План доказательства.
План доказательства.
1. Проведем 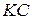 .
.
2. 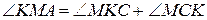 .
.
3. 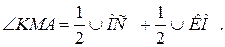
4. 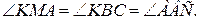
5. 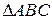 ~
~ 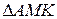 .
.
6. МК. 7. АМ. Ответ: 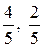 .
.
Используемые факты из теоретической карты: 1.2. №6. Окружность, построенная на стороне параллелограмма как на диаметре, проходит через середину соседней стороны и точку пересечения диагоналей. Найти углы параллелограмма.
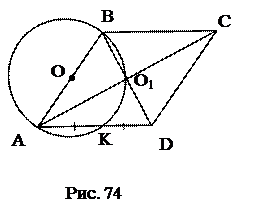 План решения.
План решения.
1. 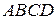 – ромб
– ромб
2. 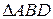 – равносторонний.
– равносторонний.
3.  .
.
4. 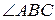 .
.
Ответ: 600, 1200.
Используемые факты из теоретической карты: 1.2.
№7. Окружность, построенная на большем основании трапеции как на диаметре, касается меньшего основания и пересекает боковые стороны, деля их пополам. Найти меньшее основание трапеции, если радиус окружности равен R.
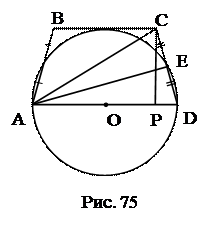 План решения.
План решения.
Дополнительные построения:
проведем АЕ, 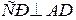 .
.
1. 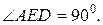
2. 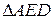 ~
~ 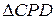 : СD2 = 4R(R - ОР).
: СD2 = 4R(R - ОР).
3. CP = R, PD = R – OP.
4. ∆CPD: OP2 + 2R∙OP – 2R2 =0, 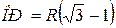 .
.
5. Трапеция ABCD – равнобедренная. ВС = 2ОР.
Ответ: 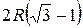 .
.
Используемые факты из теоретической карты: 1.2.
№8. Высоты остроугольного треугольника продлены до пересечения с описанной окружностью. Доказать, что отрезки этих линий от ортоцентра до окружности делятся соответственными сторонами пополам.
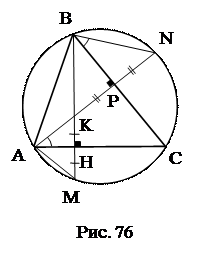
План доказательства.
Точка К – ортоцентр треугольника АВС.
Проведем BN.
1. ∆ВНС: 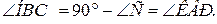
2. ∆АРС: 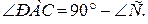
3. 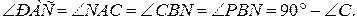
4. 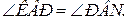 5.
5. 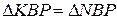 . 6. КР=PN.
. 6. КР=PN.
Аналогично доказывается, что 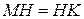 .
.
Используемые факты из теоретической карты: 1.2.
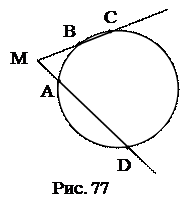
№9. Окружность разделена точками A, B, C и D так, что 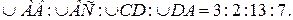 Хорды
Хорды 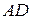 и
и 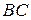 продолжены до пересечения в точке М. Найти угол АМВ.
продолжены до пересечения в точке М. Найти угол АМВ.
План решения.
1. 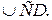
2. 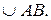
3. 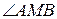 .
.
Ответ: 72°.
Используемые факты из теоретической карты: 1.3.
№ 10. На окружности взяты четыре точки. Середины образованных дуг попарно соединены отрезками. Доказать, что среди этих отрезков есть, по крайней мере, два перпендикулярных.
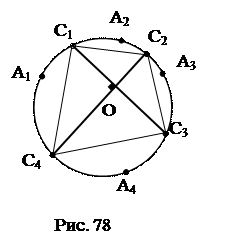
А1, А2, А3, А4 – произвольно выбранные точки,
С1, С2, С3, С4 - середины дуг А1 А2, А2 А3, А3 А4, А1А4 соответственно.
План доказательства.
1. Выразить 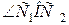 через
через  и
и 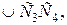 а затем через дуги
а затем через дуги 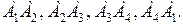
2. 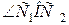
Используемые факты из теоретической карты: 1.4.
№11. В окружность вписан четырехугольник. Его противоположные стороны CD и АВ, ВС и AD продолжены до взаимного пересечения в точках N и F. Доказать, что биссектрисы углов BFA и AND перпендикулярны.
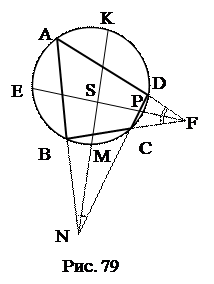
План решения.
1.  .
.
2. 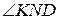 .
.
3. 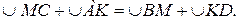
4. 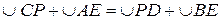 .
.
5. 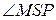 .
.
6. 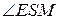 .
.
7. 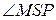 =
= 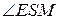 =90°.
=90°.
Используемые факты из теоретической карты:
1.3; 1.4.
№12. Через точку касания двух окружностей проведены две секущие, концы которых соединены хордами. Доказать, что эти хорды параллельны.
План доказательства.
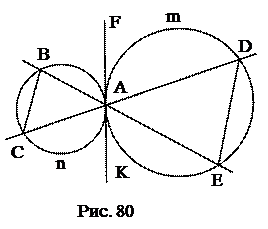 1.
1.  .
.
2. 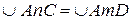 .
.
3. 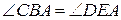 .
.
4. CB || DE.
Используемые факты из теоретической карты: 1.2; 1.5.
№13. В треугольнике АВС проведены высоты ВВ1 и СС1. Доказать, что
касательная в точке А к описанной окружности параллельна прямой В1С1.
 План решения.
План решения.
1. ÐАВС = ÐАВ1С1.
2. ÐАВС = ÐКАС.
3. АК || C1D1.
Используемые факты из теоретической карты: 1.5.
№14. Окружность проходит через вершины В, С, D трапеции ABCD и касается боковой стороны АВ в точке В. Основания трапеции а и b. Найти диагональ BD.
План решения.
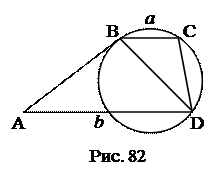 1.
1. 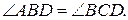
2. 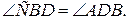
3. 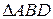 ~
~ 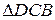 .
.
4. 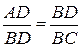 .
.
5. 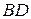 . Ответ:
. Ответ: 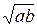 .
.
Используемые факты из теоретической карты: 1.2; 1.5.
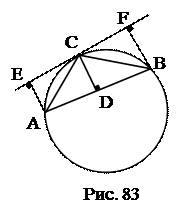
№15. Из точки С окружности на хорду АВ опущен перпендикуляр CD. Из концов хорды опущены перпендикуляры АЕ и BF на касательную к окружности в точке С. Доказать, что 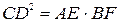 .
.
 План доказательства.
План доказательства.
1. 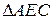 ~
~ 
2. 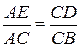 .
.
3. АЕ.
4. 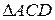 ~
~ 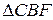 .
.
5. 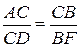 . 6. BF. 7.
. 6. BF. 7. 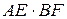 .
.
Используемые факты из теоретической карты: 1.2; 1.5.
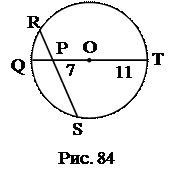
№16. Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см.
Через эту точку проведена хорда длиной 18 см. Каковы длины отрезков, на
которые делится хорда точкой Р?
План решения.
 1.
1.  .
.
2.  ∙РТ.
∙РТ.
3. 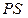 ∙
∙ 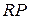 =
= 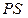 ∙ (18 –
∙ (18 – 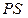 ).
).
4.  ∙РТ=
∙РТ= 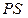 ∙
∙ 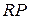 .
.
5. 
Ответ: 6 и 12. Используемые факты из теоретической карты: 2.1.
№17. АС и ВD – диагонали ромба АВCD. Окружность описанная около
треугольника ABD, пересекает большую диагональ АС в точке Е. Определить диагонали ромба, если АВ = 20 см, СЕ = 7 см.
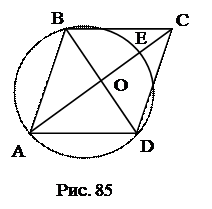 План решения.
План решения.
1. АО2+ОВ2=АВ2.
2. АО∙ОЕ=ОВ2, АО∙(АО – ЕС) = ОВ2.
3. Решить систему уравнений
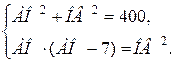
Ответ: 32 см, 24 см.
Используемые факты из теоретической карты: 2.1.
№ 18. Через точку Р диаметра АВ данной окружности проведена хорда CD, образующая с диаметром АВ угол 60°. Вычислить радиус окружности R, если
СР = а и PD = b.
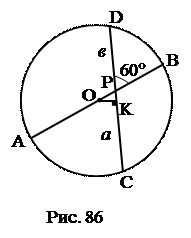 Дополнительное построение: ОК ^ DC.
Дополнительное построение: ОК ^ DC.
План решения.
1.СК. 2. КР. 3. ОР (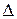 ОКР).
ОКР).
4. Выразить АР через ОР и R.
5. Выразить РВ через ОР и R.
6.Составить равенство АР·РВ = СР·РD.
7.Выразить R из составленного равенства.
Ответ: 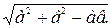
Используемые факты из теоретической карты: 2.1;
№19. Из внешней точки проведена к окружности секущая длиной 12 см и
касательная, длина которой составляет два внутренних отрезка секущей.
Определить длину касательной.
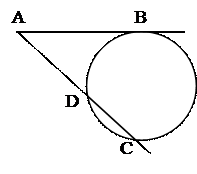 План решения.
План решения.
1. Выразить AD через АС и DС.
2. Выразить АВ через DС.
3. Составить уравнение.
|
Ответ: 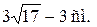
Используемые факты из теоретической карты: 2.2.
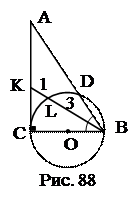
№20. Полуокружность, построенная на меньшем катете, как на диаметре, делит биссектрису острого угла, прилежащего к этому катету, в отношении 1:3. Найти углы треугольника.
 План решения.
План решения.
1. КС – касательная, КВ – секущая,
выразить КС (в частях).
2. sin 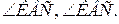
3.  Ответ: 300, 600.
Ответ: 300, 600.
Используемые факты из теоретической карты: 2.2.
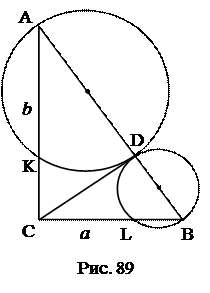
№21. Катеты прямоугольного треугольника равны а и b. На отрезках гипотенузы, определенных основанием перпендикуляра, опущенного на гипотенузу из
вершины прямого угла, описаны как на диаметрах окружности. Найти длины отрезков катетов, находящихся внутри этих окружностей.
 План решения.
План решения.
1. 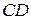 .
.
2. КС (СD – касательная, СА – секущая).
3. АК.
4. Аналогично LB.
Ответ:  . Используемые факты из теоретической карты: 2.2.
. Используемые факты из теоретической карты: 2.2.
№22. На боковой стороне АВ равнобедренного треугольника как на диаметре построена окружность. Окружность пересекает основание АС в точке М, а
боковую сторону ВС в точке N. Найти длины отрезков СN и NM, если
АС=а, АВ=b.
План решения. 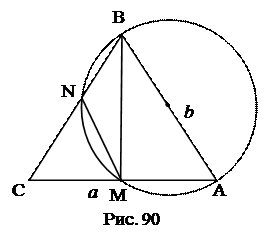
1. 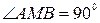 .
.
2. 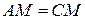 .
.
3. 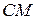 .
.
4. CN∙CB=AC∙CM, CN.
5. MA=NM.
Ответ: 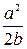 ,
, 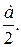
Используемые факты из теоретической карты: 1.2; 2.3.
 АDВ
.
АDВ
.