VIII.3. Задачи к теоретической карте № 8

№1. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны. Доказать.

План доказательства.

1. Параллелограмм MNPK – ромб.

2. AC=BD.

Используемые факты из теоретической карты: 1.1.

 

№2. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6 см. Длина отрезка, соединяющего середины оснований равна 4,5 см. Найти площадь трапеции.

 

 

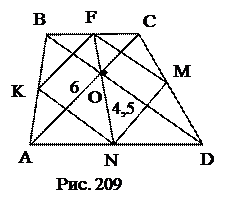Дополнительные построения:

KFMN – параллелограмм, вершины

которого – середины сторон трапеции.

План решения.

1. KFMN – прямоугольник.

2. KF. 3. KN. 4. S_KFMN. 5. S_АВСD.

Ответ: см. Используемые факты из теоретической карты: 1.1; 1.2.

 

№3. Доказать, что отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке.

Проиллюстрируем фрагменты условия задачи на двух чертежах.

 

 

План доказательства.

О – точка пересечения отрезков, соединяющих середины противоположных сторон четырехугольника ABCD (рис. 210.1). L – середина диагонали АС, F- середина диагонали BD (рис. 210.2).

1. О – середина NK. 2. NLKF – параллелограмм. 3. О – середина NK и LF.

4. Вывод.

Используемые факты из теоретической карты: 1.1.

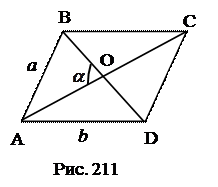
№4. Найти площадь параллелограмма, если длины его сторон равны a и b, а угол между диагоналями, противолежащий стороне длины а, равен .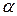

 

План решения.

1. Выразить а² через АО и ОВ.

2. Выразить b² через АО и OD.

3. Выразить из (1) и (2) АО∙ОВ и АС∙BD.

4. S_ABCD

Ответ: .

Используемые факты из теоретической карты: 2.

№5. Сумма диагоналей ромба равна m, а его площадь S. Найти сторону ромба.

План решения.

1. Выразить m² через АС и BD.

2. Выразить АС∙ BD через S.

3. Выразить АС²+ BD² через m и S.

4. Выразить АО²+ОВ² через m и S.

5. АВ.

Ответ:

Используемые факты из теоретической карты: 2.

№6. В ромб с острым углом 60°вписан четырёхугольник так, что его вершинами являются основания высот, проведённых из точки пересечения диагоналей ромба к его сторонам, Найти отношение площади четырёхугольника к площади ромба.

План решения.

Пусть сторона ромба равна а.

1. Выразить NQ через а.

2. Выразить S_MNPQ через NQ, а затем через а.

3. Выразить S_ABCD через а.

4. Hайти искомое отношение.

Ответ: 0,375.

Используемые факты из теоретической карты: 2.

№7. Доказать, что площадь треугольника равна произведения двух медиан на синус угла между ними.

План доказательства.

1. Выразить площадь треугольника ВС₁А₁

через площадь данного треугольника S.

2. Выразить площадь четырехугольника

АС₁А₁С через его диагонали.

3. Выразить площадь данного треугольника

через площадь четырехугольника АС₁А₁С

и площадь треугольника ВС₁А₁.

Используемые факты из теоретической карты: 2.

№8. Диагональ трапеции вписанной в круг радиуса R, образует с ее боковыми сторонами углы 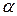и . Найти площадь трапеции.

План решения.

1. ÐODC в ∆COD.

2. ÐCOD в ∆COD.

3. ÐAOD.

4. ÐODA (∆ODA).

5. ÐADC ((1) + (4)).

6. АС (по теореме синусов ∆ACD).

7. S_ABCD.

Ответ: .

Используемые факты из теоретической карты: 2.

№9. Четырехугольник разделен диагоналями на четыре треугольника. Наименьшие площади трех из них равны 10, 20 и 30. Найти площадь данного четырехугольника.

План решения.

1. Установить соответствие между треугольниками и площадями.

2. Найти площадь четвертого треугольника.

3. S_ABCD.

Ответ: 120.

Используемые факты из теоретической карты: 3.

№10. В трапеции ABCD(AВ||CD). О – точка пересечения диагоналей АС и BD. Площади треугольников АВО и CDO равны соответственно 10 и 40. Найти
площадь трапеции.

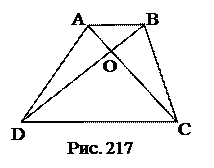План решения.

1. S_∆AOD= S_∆BOC.

2. S_∆AOD.

3. S_ABCD.

Ответ: 90.

 

Используемые факты из теоретической карты: 3.

 

№11. Площадь трапеции равна 3, основания относятся как 1:2. Найдите площади треугольников, на которые трапеция разделена диагоналями.

План решения.

S_∆AOВ= S₁, S_∆BOC= S₂, S_∆СOD= S₃, S_∆AOD= S₄.

1. S₁= S₃. 2. S₄= 4S₂. 3. S₁=2S₂.

4. 2S₁+ S₁+2S₁=3. 5. S₁, S₂, S₃, S₄.

Ответ:

Используемые факты из теоретической карты: 3.

№12. В равнобокую трапецию вписана окружность радиуса 2. Найти площадь трапеции, если длина боковой стороны равна 10.

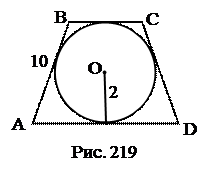План решения.

1. ВС+AD.

2. Р_ABCD.

3. S_ABCD.

Ответ: 40.

Используемые факты из теоретической карты: 4,5.

 

№13. Около окружности, радиус которой равен 1,2 см описан четырехугольник ABCD, у которого АВ=3 см, ВС=2 см, AD=4 см. Найти площадь этого четырехугольника.

План решения.

1. CD.

2. S_ABCD.

Ответ: 7,2 см²

Используемые факты из теоретической карты: 5, 4.

№14. Около круга описана равнобедренная трапеция, площадь которой равна 32 см². Найти стороны трапеции, если угол при большем основании равен 30⁰.

План решения.

1. Выразить ВС+AD, ВF, S_ABCD через АВ.

2. АВ. 3. AD+BC. 4. AF. 5. BC, AD.

Ответ: 8 см, см, см, 8 см.

Используемые факты из теоретической карты: 5.

 

№15. Равнобедренная трапеция ABCD (AD||BC, AD>BC) описана около окружности с центром О. О₁ – точка пересечения диагоналей трапеции. Площади треугольников АО₁В и АОВ равны 3 и 4. Найти углы трапеции.

Проиллюстрируем фрагменты условия задачи на двух чертежах.

 

 

План решения.

1. АВ∙ r. 2. Выразить полупериметр ABCD через АВ. 3. S_ABCD.

4. Составить систему уравнений (Рис. 222.2).

5. S₂, S₄. 6. AD: ВС. 7. Выразить AD через ВС. 8. Выразить АК через ВС.

9. Выразить АВ через ВС. 10. АК:АВ=cos

Ответ: 60⁰, 120⁰.

Используемые факты из теоретической карты: 3, 4, 5.

№ 16. В четырехугольнике проведены все биссектрисы внутренних углов. Доказать, что пересечением биссектрис образовался четырехугольник, около которого можно описать окружность.

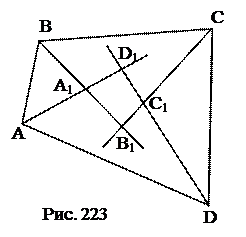План доказательства.

1. ÐВВ₁С выразить через ÐВ иÐС четырехугольникаABCD.

2. ÐАD₁D выразить через ÐA иÐD четырехугольникаABCD.

3. ÐВВ₁С +ÐАD₁D =180⁰.

Используемые факты из теоретической карты: 6.

№17. Из точки М, лежащей вне окружности, проведены два луча, пересекающие окружность в точках А, В, С и D. Доказать, что треугольники АМС и DMB подобны.

 

 

План доказательства.

1. .

2. .

3. .

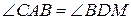4. ∆АМС~∆DMВ.

Используемые факты из теоретической карты: 6.

№18. Через середину С дуги АВ проведены прямые CD и CE, пересекающие хорду АВ в точках H и F. Доказать, что около четырехугольника DHFE можно описать окружность.

План решения.

1.

2. .

3. .

4. Вывод.

Используемые факты из теоретической карты: 6.

 

№19. Через вершину С треугольника АВС проведены его внутренняя биссектриса CD и внешняя биссектриса. Из вершины В проведен перпендикуляр к стороне АВ, пересекающий внешнюю биссектрису в точке К. Доказать, что около четырехугольника CDBK можно описать окружность (точка D лежит на стороне АВ)

План доказательства.

CD – биссектриса внутреннего угла АСВ,

СК – биссектриса внешнего угла DCB.

1. ÐDCK=90⁰.

2. ÐDCK+ÐDBK=180⁰.

3. Вывод.

Используемые факты из теоретической карты: 6.

IX. ТРАПЕЦИЯ И ПАРАЛЛЕЛОГРАММ