V.3. Задачи к теоретической карте № 5

№1. В треугольнике АВС проведена медиана АМ. Найти площадь треугольника АВС, если АС= , ВС=10,

План решения

Первый способ.

1. МС.

2. АМ.

3. S_∆_AMC.

4. S_∆_ABC.

Используемые факты из теоретической карты: 2.

Второй способ.

1. МС. 2. АМ. 3. Sin ÐACM. 4. S_∆_ABC. Ответ: 21.

Используемые факты из теоретической карты: 1.

№2. Найти расстояние от точки пересечения медиан прямоугольного
треугольника до его гипотенузы, равной 25, если один из катетов равен 20.

План решения.

Первый способ.

1. СВ.

2. S_∆АВС.

3. CH.

4. ∆ОС₁К~∆С₁СН.

5. Коэффициент подобия ∆ОС₁К и ∆С₁СН.

6. OK.

Ответ: 4.

Используемые факты из теоретической карты: 5.

Второй способ.

1. СВ.

4. ОК.

Используемые факты из теоретической карты: 6.

№3. В треугольнике АВС на основании АС взяты точки P и Q так, что AP<AQ. Прямые BP и BQ делят медиану AM на 3 равные части. Известно, что PQ= 3. Найти AC.

План решения.

1. О – точка пересечения медиан.

2. ОКêêВР.

3. РК: КQ.

4. РК, КQ. 5. АР=РК. 6. AQ. 7. АС.

Ответ: 10.

Используемые факты из теоретической карты: 4, 5.

№4. В треугольнике АВС проведены медианы BD и СЕ, G – точка их пересечения. Доказать, что треугольник BCG равновелик четырехугольнику ADGE.

План доказательства.

1. S_∆_BGC= .

2. AG – часть медианы ∆ABC.

3. S _ADGE= .

4. Вывод.

Используемые факты из теоретической карты: 4, 6.

№5. Основание равнобедренного треугольника равно см, а медиана,
проведенная к боковой стороне, 5 см. Найти длины боковых сторон.

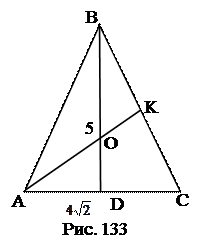План решения.

1. Проведём медиану BD.

2. AD.

3. АО.

4. ОD.

5. ВD.

6. АВ. Ответ: 6 см.

Используемые факты из теоретической карты: 1, 4, 7.2.

№. 6. В окружность вписан треугольник, одна из сторон которого равна 21 см. Параллельно этой стороне, через точку пересечения медиан, проведена хорда. Отрезки хорды, расположенные вне треугольника, равны 8 и 11 см. Определить неизвестные стороны треугольника.

План решения.

1. ~ .

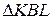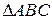2. Коэффициент подобия.

3. . 4. 5.

6. Выразить через ВС.

7. 8. ВС.

9. Аналогично .

Ответ: 30 см, 33 см.

Используемые факты из теоретической карты: 5.

№7. На каждой медиане треугольника взята точка, делящая медиану в
отношении 3:1, считая от вершины. Во сколько раз площадь треугольника с вершинами в этих трех точках меньше площади исходного треугольника?

АА₁, ВВ₁, СС₁ – медианы в ∆АВС,

О – точка их пересечения.

Построение.

1. Проведем А₁С₁, К – середина ВВ₁.

2. В₂ – середина КВ₁, ВВ₂: В₂В₁ = 3:1.

3. Аналогично строим точки А₂, С₂.

4. ∆А₂В₂С₂.

План решения.

1. ОВ₁= 2. ОВ₂=

4. 5. 6.

Ответ: в 64 раза.

Используемые факты из теоретической карты: 4, 5.

№8. В треугольнике АВС медианы, опущенные на стороны АС и ВС взаимно перпендикулярны. АС=8, ВС=6. Найти длину стороны АВ треугольника АВС.

План решения.

1. АА₁² выразить через АВ².

2. ВВ₁² выразить через АВ².

3. АО².

4. ОВ².

5. АВ.

Ответ: .

Использованные факты из теоретической карты: 3, 5.

№9. Числа m_a, m_b и m_c выражают длины медиан некоторого треугольника.
Доказать, что если выполняется равенство 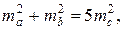то треугольник
является прямоугольным.

План решения.

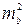1. . 2. . 3. .

4. привести к виду

5. Вывод.

Использованные факты из теоретической карты: 3.

№10. В треугольнике АВС со сторонами АВ=8, ВС=14 и АС=18 проведена
медиана BD, на которой выбрана точка Е так, что ВЕ:ED=8:9. Найти расстояние от точки Е до вершины А.

План решения.

1. АЕ – биссектриса ÐBAD.

2. BD². 3. BD. 4. ВЕ. 5. ED.

6. AE². 7. AE. Ответ: .

Используемые факты из теоретической

карты: 3, 4.

№11. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найти площадь треугольника.

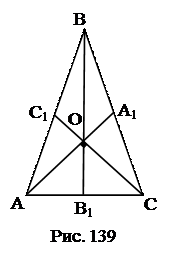
– медианы в ∆АВС.

План решения.

1. ОВ₁=В₁С.

2. ОВ=2ОВ₁

3. ВВ₁ выразить через В₁С.

4. ВВ₁

5. S_∆АВС.

Ответ: 3.

Используемые факты из теоретической карты: 5, 7.1, 7.2.

№12. В треугольнике АВС проведены медианы АК и СМ. Оказалось, что 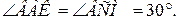Доказать, что треугольник АВС равносторонний.

АК, СМ – медианы треугольника АВС.

План доказательства.

Рисунок 140.

1. ОМ∙ОА=ОК∙ОС. 2. ОМ:ОА=ОК:ОС. 3. ОМ=ОК. 4. СМ=АК. 5. АВ=ВС.

6. Коррекция чертежа.

Рисунок 141.

Проведём ОР 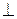АВ.

6. 7. 8.ОР=ОМ. 9. МО 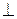АВ, СМ 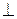АВ. 10. ВС= АС.

11. АВ=ВС=АС.

Используемые факты из теоретической карты: 5, 6, 7.1, 7.2.

№13. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна m и делит прямой угол в отношении 1: 2. Найти стороны треугольника.

План решения.

1. АСС₁, С₁СВ.

2. ∆ АСС₁– равносторонний.

3. СВ.

4. АВ.

5. АС.

Ответ: m, , 2 m.

Используемые факты из теоретической карты: 8.

№14. Определить острые углы прямоугольного треугольника, если медиана, проведенная к его гипотенузе, делит прямой угол в отношении 1:2.

Ответ: 60⁰, 30⁰.

№15. Доказать, что высота и медиана прямоугольного треугольника, проведенные к гипотенузе образуют угол, равный разности острых углов треугольника.