№1. В треугольник вписана окружность радиуса 3 см. Вычислить длины сторон треугольника, если одна из них разделена точкой касания на отрезки с длинами 4 см и 3 см.
 План решения.
План решения.
1. 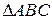 :
: 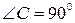 .
.
2. Выразить ВС и АВ через ВМ.
3. ВМ.
4. ВС, АВ.
Ответ: 7см, 24 см, 25 см.
Используемые факты из теоретической карты: 2.
№2. В параллелограмме со сторонами 2 и 4 проведена диагональ, равная 3. В каждый из получившихся треугольников вписано по окружности. Найти
расстояние между центрами окружностей.
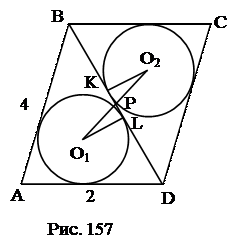 План решения.
План решения.
1. S∆BCD. 2. P∆BCD. 3. O2K = r.
4. ВК. 5. BP. 6. KP.
7. O2P. 8.  .
.
Ответ:  .
.
Используемые факты из теоретической
карты: 3, 6.
№3. Периметр параллелограмма ABCD равен 26 см. Величина угла АВС равна 1200. Радиус окружности, вписанной в треугольник BCD равен 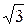 . Найти длины сторон параллелограмма (AD>AB).
. Найти длины сторон параллелограмма (AD>AB).
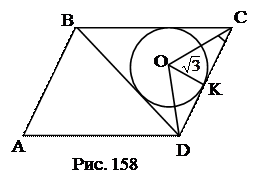 План решения.
План решения.
1. 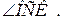
2. 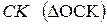 .
.
3. Выразить СК через ВD (∆DCВ).
4. 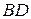 (из (1) и (2)).
(из (1) и (2)).
5. ВС.
Ответ: 5см, 8 см.
Используемые факты из теоретической карты: 1, 3.
№4. В треугольник со сторонами 6 см, 10 см, 12 см вписана окружность. К
окружности проведена касательная так, что она пересекает две большие стороны. Найти периметр отсеченного треугольника.
 План решения.
План решения.
1.  .
.
2. 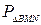 .
.
Ответ: 16 см.
Используемые факты из теоретической карты: 3, 5.
№5. В равнобедренный треугольник с основанием 12 см вписана окружность и к ней проведены три касательные так, что они отсекают от данного треугольника три малых треугольника. Сумма периметров малых треугольников равна 48 см. Найти боковую сторону данного треугольника.
 План решения.
План решения.
1. Р 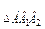 выразить через ВК.
выразить через ВК.
2. Р 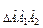 выразить через АК.
выразить через АК.
3. Р 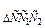 выразить через СМ.
выразить через СМ.
4. Составить и решить уравнение.
Ответ: 18 см.
Используемые факты из теоретической карты: 5.
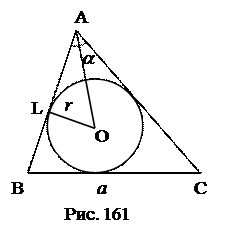
№6. Найти площадь треугольника по углу 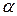 , стороне и радиусу вписанной
, стороне и радиусу вписанной
окружности  .
.
 План решения.
План решения.
1. 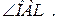
2. Полупериметр 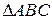 .
.
3. 
Ответ: 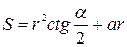 .
.
Используемые факты из теоретической карты: 1, 4, 6.
№7. Доказать, что произведение длин отрезков, на которые гипотенуза
прямоугольного треугольника делится точкой касания вписанной в него окружности, равна площади треугольника.
 План доказательства.
План доказательства.
1.  .
.
2.  .
.
3. 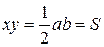 .
.
Используемые факты из теоретической карты: 3.
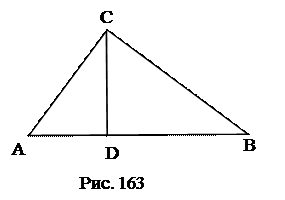
№8. В прямоугольном треугольнике АВС  проведена высота
проведена высота 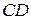 . Доказать, что
. Доказать, что 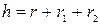 , где
, где 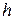 – длина высоты
– длина высоты 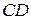 ,
, 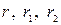 – радиусы окружностей, вписанных в треугольники
– радиусы окружностей, вписанных в треугольники 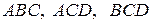 соответственно.
соответственно.
 План доказательства.
План доказательства.
1. Выразить r через стороны ∆АВС.
2. Выразить r1 через стороны ∆АСD.
3. Выразить r2 через стороны ∆BCD.
4. 
Используемые факты из теоретической карты: 7.
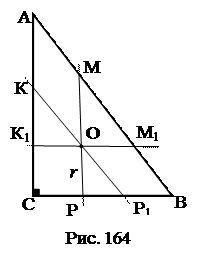
№9. Впрямоугольный треугольник с катетами 6 см и 8 см вписана окружность. Через центр окружности проведены прямые, параллельные сторонам
треугольника. Вычислить длины средних отрезков на сторонах треугольника, которые отсекаются проведенными прямыми.
 План решения.
План решения.
1. АB. 2. ОР = r. 3. ∆АВС ~ ∆ОР1Р. 4. РР1.
5. Аналогично КК1. 6. Р1В, ОМ1. 7. АК. 8.ММ1.
Ответ: 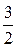 см,
см, 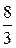 см,
см,  см.
см.
Используемые факты из теоретической карты: 7.
№10. В прямоугольном треугольнике высота, проведенная к гипотенузе, равна 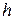 , радиус вписанной окружности равен
, радиус вписанной окружности равен  . Найти гипотенузу.
. Найти гипотенузу.
 План решения.
План решения.
1. Выразить  через
через  и
и  .
.
2. Выразить  через
через  и
и 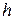 .
.
3. Из (1) и (2) найти  . Ответ:
. Ответ: 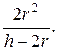 Используемые факты из теоретической карты: 8
Используемые факты из теоретической карты: 8
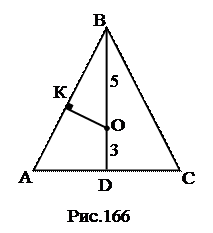
№11. В равнобедренном треугольнике центр вписанной окружности делит
высоту, проведенную к основанию, на отрезки 5 и 3, считая от вершины. Найти радиус описанной окружности.
 План решения.
План решения.
1. ВК.
2. 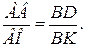
3. АВ.
4. sinA.
5. R.
Ответ: 6,25. Используемые факты из теоретической карты: 9.
№12. Доказать, что окружность, проходящая через ортоцентр треугольника и две его вершины, равна окружности, описанной около треугольника.
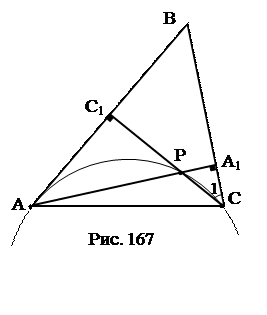
План доказательства.
1. 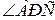 =90° +
=90° + 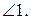
2. 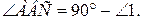
3. 
4. R=R1, где R и R1 – радиусы окружностей, описанных около ∆АВС и ∆АРС соответственно.
Используемые факты из теоретической
карты: 9.
№13. Найти радиус окружности, описанной около равнобокой трапеции с
основаниями 2 и 14 и боковой стороной 10.
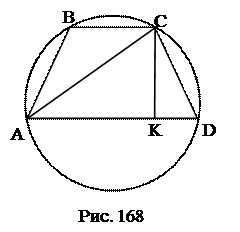
План решения.
Первый способ.
1. КD. 2. СК. 3. 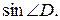
4. АК. 5. АС. 6. R.
Используемые факты из теоретической карты: 9.
Второй способ.
1. KD. 2.AK. 3. CK. 4. AC. 5. 
6.  .
.
Ответ: 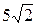 .
.
Используемые факты из теоретической карты: 10.
Замечание. Радиус окружности, описанной около трапеции АВСD и
треугольника АСD совпадают.
№14. Высота равнобочной трапеции равна 14 см, а основания равны 16 см и 12 см. Определить площадь описанного круга.
Ответ: 10 см.
№15. Доказать, что во всяком треугольнике произведение двух сторон равно произведению диаметра описанной окружности на высоту, опущенную на
третью сторону.
План доказательства.
1. Выразить из формулы 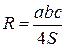 произведение сторон аb.
произведение сторон аb.
2. 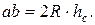
Используемые факты из теоретической карты: 10.
№16. В треугольнике АВС проведена высота BD. Точка Е – середина ВС.
Вычислить радиус круга, описанного около треугольника BDE, если АВ=30 см, ВС=26 см и АС=28 см.
 План решения.
План решения.
1.S∆ABC. 2.BD. 3.BE.
4.DE. 5. S∆DBE. 6.R.
Ответ: 16,9 см2.
Используемые факты из теоретической карты: 10
№17. Катеты прямоугольного треугольника равны 6 см и 8 см. Найти расстояние от центра вписанной в треугольник окружности до центра описанной около него окружности.
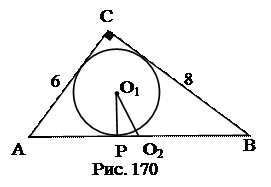 План решения.
План решения.
1.  . 2. АР. 3.
. 2. АР. 3.  .
.
4. РО2. 5. РО1. 6.  .
.
Ответ: 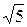 .
.
Используемые факты из теоретической карты: 3, 7, 12.
№18. Катеты прямоугольного треугольника равны 6 см и 8 см. Через середину меньшего катета и середину гипотенузы проведена окружность, касающаяся большего катета. Найти площадь круга, ограниченного этой окружностью.

План решения.
1. МК. 2.DC. 3.DK. 4.DM=DK.
5. DF. 6. S∆KDM. 7. Rкруга. 8. Sкруга.
Ответ: 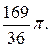
Используемые факты из теоретической карты: 10.
№19. Доказать, что в прямоугольном треугольнике сумма диаметров вписанной и описанной окружностей равна сумме катетов.
План доказательства.
1. Выразить радиус вписанной окружности r через стороны треугольника.
2. Выразить радиус описанной окружности R через стороны треугольника.
3. Проверить справедливость равенства, которое требуется доказать.
Используемые факты из теоретической карты: 7, 10.
№20. Найти радиус окружности, описанной около прямоугольного треугольника, если радиус окружности, вписанной в этот треугольник, равен 3 см, а меньший катет равен 10 см.
План решения.
1. Выразить радиус вписанной окружности r через стороны треугольника.
2. Составить равенство по теореме Пифагора.
3. Составить и решить систему уравнений.
4. Выразить радиус описанной окружности R.
Ответ: 
Используемые факты из теоретической карты: 7, 10.
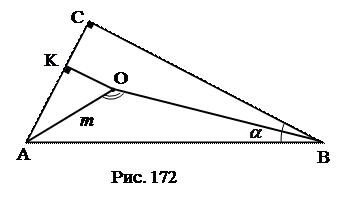
№21. Найти площадь прямоугольного треугольника с острым углом 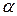 , если известно, что расстояние от вершины другого острого угла до центра
, если известно, что расстояние от вершины другого острого угла до центра
вписанной окружности равно m.
 План решения.
План решения.
1. 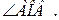 2.
2. 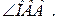 3. АВ.
3. АВ.
4.  5.ОК. 6. S∆ABC.
5.ОК. 6. S∆ABC.
Ответ: 0,5 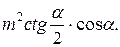
Используемые факты из теоретической карты: 9, 11, 12, 13.