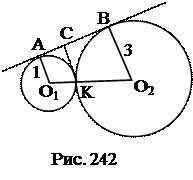
№1. Две окружности радиусов R =3 см и r =1 см касаются внешним образом. Найти расстояние от точки касания окружностей до их общей касательной.
 План решения.
План решения.
1. О1АВО2 – трапеция.
2.  .
.
3. КС.
Ответ: 1,5 см.
Используемые факты из теоретической карты: 1.
№2. Прямая, параллельная основаниям трапеции, проходит через точку пересечения ее диагоналей. Найти длину отрезка этой прямой, заключенного между боковыми сторонами трапеции, если основания трапеции равны 4 см и 12 см.
 План решения.
План решения.
1. ∆AOD~∆COB.
2.  .
.
3.  .
.
4.  . Ответ: 6 см.
. Ответ: 6 см.
Используемые факты из теоретической карты: 1.
№3. Основания трапеции равны 1 см и 7 см. Найти длину отрезка, параллельного основаниям трапеции и делящего ее площадь на две равновеликие части.
 Введём обозначения:
Введём обозначения:
 – длина высоты трапеции
– длина высоты трапеции  ,
,
 – длина высоты трапеции
– длина высоты трапеции  ,
,
 – отрезок, делящий трапецию на две равновеликие части. Пусть длина
– отрезок, делящий трапецию на две равновеликие части. Пусть длина  = х.
= х.
План решения.
1. Выразить SPBCQ через х и  .
.
2. Выразить SAPQD через х и  .
.
3. Составить уравнение SPBCQ =SAPQD.
4.  .
.
5. Выразить х через  и
и  .
.
6. Составить систему уравнений из (3) и (5) и решить её относительно  . Ответ: 5 см.
. Ответ: 5 см.
Используемые факты из теоретической карты: 1.
№4. Диагональ равнобокой трапеции равна 10 см, а площадь равна 48 см2. Найти высоту трапеции.
 План решения.
План решения.
1. Выразить высоту СН через АН.
2. Выразить площадь трапеции через АН и СН.
3. Из (1) и (2) составить систему уравнений.
4. Решить систему уравнений.
Ответ: 6 см или 8 см.
Используемые факты из теоретической карты: 2.
№5. Найти площадь равнобокой трапеции, если ее высота равна h, а боковая сторона видна из центра описанной окружности под углом 600.
 План решения.
План решения.
1. 
2. Выразить AH через h.
3. SABCD.
Ответ:  .
.
Используемые факты из теоретической карты: 2.
№6. В окружность радиуса  вписана трапеция, боковая сторона которой стягивает дугу в 900. Найти площадь трапеции, если разность длин ее оснований равна 2 а.
вписана трапеция, боковая сторона которой стягивает дугу в 900. Найти площадь трапеции, если разность длин ее оснований равна 2 а.
 План решения.
План решения.
Первый способ.
1. Выразить АВ через R. 2. АК.
3. ВК. 4.  5. KD. 6. SABCD.
5. KD. 6. SABCD.
Используемые факты из теоретической карты: 2.
Второй способ.
1. Выразить АВ через R. 2. АК. 3. ВК. 4.  ^
^ 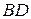 . 5. SABCD.
. 5. SABCD.
Используемые факты из теоретической карты: 4.
Ответ:  .
.
№7. В окружность вписана трапеция, боковая сторона которой равна 15, средняя линия 16, а большее основание является диаметром окружности. Определить площадь трапеции.
 План решения.
План решения.
1. KD.
2. 
3. АК.
4. ВК.
5. SABCD.
Ответ 192.
Используемые факты из теоретической карты: 2.
№8. В равнобокую трапецию вписана окружность и около нее описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно 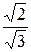 . Найти углы трапеции.
. Найти углы трапеции.
 Пусть ВН – высота трапеции, радиус окружности, описанной около данной трапеции (и около треугольника ABD) равен R,
Пусть ВН – высота трапеции, радиус окружности, описанной около данной трапеции (и около треугольника ABD) равен R,  .
.
План решения.
1. AB=HD. 2. sin α=tg β. 3. 
4.  5.
5. 
6. Найти sinα, решив систему уравнений 7. α. 8.  .
.

Ответ: 450, 1350.
Используемые факты из теоретической карты: 2.
№9. Около окружности радиуса r описана равнобокая трапеция, меньшее
основание которой равно 2 а. Найти диагональ трапеции.
 План решения.
План решения.
1. 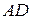 .
.
2.  .
.
3. 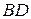 .
.
Ответ:  .
.
Используемые факты из теоретической карты: 3, 2.
№10. Около окружности радиуса 5 см описана равнобокая трапеция. Расстояние между точками касания боковых сторон равно 8 см. Найти площадь трапеции.
 План решения.
План решения.
Пусть  . E, F – точки касания.
. E, F – точки касания.
1.  êê
êê 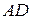 .
.
2. MN= 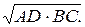
3. Выразить MN через х и у.
 4.
4.  .
.
5.  6. Выразить EF через х и у.
6. Выразить EF через х и у.
7. Решить систему уравнений (3, 5). 8. SABCD.
Ответ: 125 см2.
Используемые факты из теоретической карты: 3, 1.
№11. Из точки пересечения диагоналей равнобокой трапеции на боковую сторону опущен перпендикуляр, который делит ее на отрезки длиной 3,2 см и 1,8 см, считая от нижнего основания. Найти площадь трапеции, если длина указанного перпендикуляра есть среднее геометрическое длин отрезков боковой стороны.
 План решения.
План решения.
1.  ^
^ 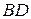 . 2.
. 2.  3.
3.  4.
4. 
5.  6.
6.  . 7.
. 7. 
Ответ: 24,5 см2.
Используемые факты из теоретической карты: 4.
№12. В равнобедренном треугольнике 
 . Через
. Через
середину  стороны
стороны  проходит прямая, которая пересекает
проходит прямая, которая пересекает 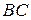 в точке
в точке  и продолжение
и продолжение  в точке
в точке 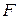 . Площади треугольников
. Площади треугольников  и
и  равны. Найти длину отрезка
равны. Найти длину отрезка  .
.
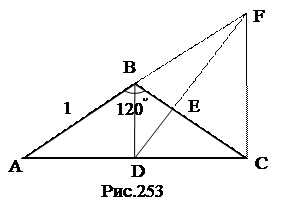 План решения.
План решения.
1. 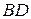 êê
êê  (
( – трапеция).
– трапеция).
2.  3.
3.  4.
4.  5. DF.
5. DF.
6.  - медианы
- медианы  . 7.
. 7.  .
.
Ответ:  .
.
Используемые факты из теоретической карты: 5.
№13. Доказать, что если два треугольника, получающиеся при продолжении сторон выпуклого четырехугольника до их пересечения, равновелики, то одна из диагоналей четырехугольника делит другую пополам.
 План доказательства.
План доказательства.
1. AC||MN.
2. Далее реализуется план доказательства
задачи № 9 из раздела II «Пропорциональные
отрезки».
Используемые факты из теоретической карты: 5.
№14. Центр круга вписанного в прямоугольную трапецию, отстоит от концов боковой стороны на 1см и 2 см. Найти площадь трапеции.
 План решения.
План решения.
1.  . 2.
. 2. 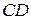 . 3.
. 3. 
4.  5.
5.  . 6.
. 6. 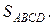
Ответ: 3,6 см2.
Используемые факты из теоретической карты: 6.
№15. В трапецию вписана окружность радиуса 6. Точка касания делит одно из оснований на отрезки 9 и 12. Найти стороны трапеции.
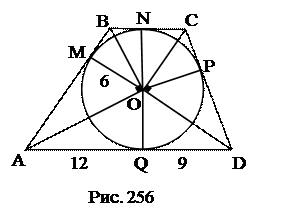 План решения.
План решения.
1.  - точка пересечения биссектрис.
- точка пересечения биссектрис.
2.  .
.
3.  . 4. МВ. 5. АВ.
. 4. МВ. 5. АВ.
6. PD. 7. СР. 8. CD
9. BN. 10. NC. 11.ВС.
Ответ: 7, 15, 21, 13.
Используемые факты из теоретической карты: 6.
№16. Около окружности описана трапеция 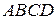 (AD||BC). Расстояние от центра окружности до вершин
(AD||BC). Расстояние от центра окружности до вершин  и
и 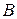 равны соответственно
равны соответственно  и
и  . Определить
. Определить  и высоту трапеции.
и высоту трапеции.
 План решения.
План решения.
1.  – точка пересечения биссектрис.
– точка пересечения биссектрис.
2.  . 3. АВ. 4.
. 3. АВ. 4. 
5.  . 6.
. 6.  . 7.
. 7. 
Ответ:  ;
;  .
.
Используемые факты из теоретической карты: 6.
№17. В параллелограмме со сторонами  и
и 
 проведены биссектрисы внутренних углов. Определить вид четырехугольника, образовавшегося при пересечении биссектрис и найти длины его диагоналей.
проведены биссектрисы внутренних углов. Определить вид четырехугольника, образовавшегося при пересечении биссектрис и найти длины его диагоналей.
 План решения.
План решения.
1.  – прямоугольник.
– прямоугольник.
2.  .
.
3.  .
.
Используемые факты из теоретической
карты: 7.
№18. Внутри параллелограмма АВСD с острым углом А и стороной AD=7,7 расположена окружность, радиус которой равен 2,4, так, что она касается сторон AD AB и ВС. Точка касания делит АВ в отношении 16: 9, считая от вершины А. Найти периметр параллелограмма.
 План решения.
План решения.
1. D АОВ:ÐАОВ=90°.
2. АК, КВ, АВ.
3 .РABCD.
Ответ: 25,4.
Используемые факты из теоретической карты: 7.
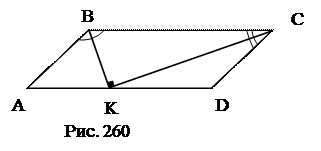
№19. Дан параллелограмм 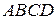 с острым углом
с острым углом  . На стороне
. На стороне 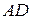 взята точка
взята точка  так, что
так, что  – биссектриса угла
– биссектриса угла  .
.  – биссектриса угла
– биссектриса угла  . Найти отношение периметра параллелограмма к радиусу окружности, описанной около треугольника
. Найти отношение периметра параллелограмма к радиусу окружности, описанной около треугольника  .
.
 План решения.
План решения.
1.  . 2.
. 2. 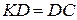 .
.
3. 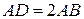 . 4.
. 4.  .
.
5.  6.
6.  .
.
7.  . Ответ: 6. Используемые факты из теоретической карты: 7.
. Ответ: 6. Используемые факты из теоретической карты: 7.
№20. Даны две концентрические окружности. Доказать, что сумма квадратов расстояний от точки одной окружности до концов диаметра другой окружности не зависит ни от выбранной точки, ни от выбранного диаметра.

Пусть О – общий центр данных окружностей,
Х – произвольная точка одной окружности,
ХР – её диаметр,
АВ – произвольный диаметр другой окружности.
План доказательства.
1. 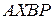 – параллелограмм.
– параллелограмм.
2.  , где
, где  – радиусы окружностей.
– радиусы окружностей.
3. Вывод.
Используемые факты из теоретической карты: 8.
№21. Доказать, что во всяком четырехугольнике сумма квадратов диагоналей вдвое больше суммы квадратов отрезков, соединяющих середины противоположных сторон.
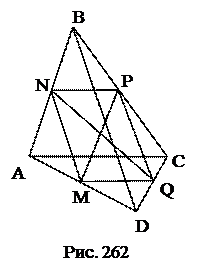 M, N, H, Q – середины сторон четырехугольника ABCD.
M, N, H, Q – середины сторон четырехугольника ABCD.
План доказательства.
1.  – параллелограмм.
– параллелограмм.
2. Выразить  через стороны параллелограмма
через стороны параллелограмма  .
.
3. Выразить стороны параллелограмма  через диагонали четырехугольника
через диагонали четырехугольника 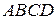 .
.
Используемые факты из теоретической карты: 8.
№22. В треугольник вписан параллелограмм так, что одна его сторона лежит на основании треугольника, а диагонали параллельны его боковым сторонам. Основание треугольника равно 45 см, а боковые стороны 39 см и 48 см. Найти стороны параллелограмма.
 План решения.
План решения.
1. 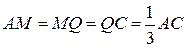 .
.
2.  ~
~  . 3.
. 3. 
4.  ~
~  5.
5.  .
.
6.  .
.
Ответ: 15 см, 25 см.
Используемые факты из теоретической карты: 8.
Х. Приложение
При решении планиметрических задач полезно знать зависимости, рассмотренные в приведённой ниже задаче [3, с.15].
Задача о четырёх отношениях.
В треугольнике АВС (рис. 264) проведены отрезки АА1 и СС1, пересекающиеся в точке О. Точки А1, С1 и О определяют четыре отношения:
1) АС1 : С1В; 2) ВА1 : А1С 3) АО: ОА1; 4) СО: ОС1. Если известны любые два из указанных отношений, то могут быть вычислены два других.
 Введём обозначения:
Введём обозначения:
Пусть 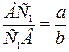 (1);
(1);
 (2);
(2);
 (3);
(3);
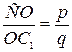 (4).
(4).
Решение задачи сводится к рассмотрению шести случаев, приведённых в таблице
| № п/п | Номера заданных отношений | Номера вычисляемых отношений |
| 1, 2 | 3, 4 | |
| 1, 3 | 2, 4 | |
| 1, 4 | 2, 3 | |
| 2, 3 | 1, 4 | |
| 2, 4 | 1, 3 | |
| 3, 4 | 1, 2 |
Рассмотрим первый случай.
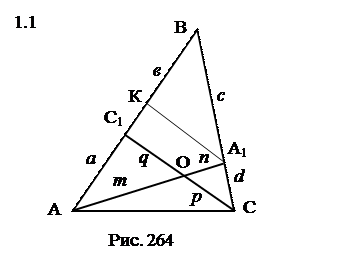 Дано:
Дано: 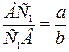 ,
,  .
.
Найти:  .
.
Дополнительное построение.
Проведём А1К || СС1
Решение
1) 
(использовано свойство пропорциональных отрезков на сторонах угла).
2) 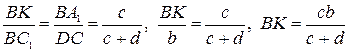
(использовано подобие треугольников)
3) Из (1) и (2)  .
.
1.2. Дано: 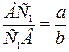 ,
,  . Найти:
. Найти: 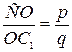 .
.
Результат получится, если переобозначить вершины А и С, то есть  .
.
Аналогично могут быть получены два искомых отношения по двум известным отношениям и в остальных случаях. Причём можно заметить, что задачи 2 и 3, 4 и 5 по существу одинаковы.
В таблице приведены выражения для вычисления искомых отношений.
| №п/п | 
| 
| 
| 
|

| 
| 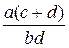
| 
| |

|  
| 
| 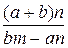
| |
 
| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
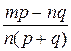
| 
| 
| 
|
Рассмотрим примеры задач, при решении которых используются полученные результаты.
 № 1. Точка D принадлежит стороне АС треугольника АВС и делит эту сторону в отношении AD:DC=3:2. На отрезке BD выбрана точка Е так, что BE:ED=4:1. В каком отношении прямая АЕ делит площадь треугольника АВС?
№ 1. Точка D принадлежит стороне АС треугольника АВС и делит эту сторону в отношении AD:DC=3:2. На отрезке BD выбрана точка Е так, что BE:ED=4:1. В каком отношении прямая АЕ делит площадь треугольника АВС?
Решение
Пусть 
По условию задачи известны отношения 
 . Необходимо вычислить отношение
. Необходимо вычислить отношение 
 . Пользуясь четвёртой
. Пользуясь четвёртой
строкой таблицы, получим  =
=  .
.
Прямая АЕ делит треугольник АВС на два треугольника ABF и AFC
с равными высотами, проведёнными из вершины А. Следовательно, их площади относятся как BF к FC. Искомое отношение площадей равно 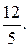
В решении приведённых ниже задач также используются табличные отношения.
№ 2. На медиане BD треугольника АВС, площадь которого равна S, выбрана точка Е так, что DE =  BD. Прямая АЕ делит пересекает сторону ВС в точке F. Найти площадь треугольника AFC.
BD. Прямая АЕ делит пересекает сторону ВС в точке F. Найти площадь треугольника AFC.
Ответ: 
№3. В треугольнике АВС точка Е – середина биссектрисы СС1. В каком отношении прямая АЕ делит площадь треугольника АВС, если известно, что
СА: СВ = p: q?
Ответ: 
№4. В правильном треугольнике АВС со стороной а проведена средняя линия MN параллельно АС. Через точку А и середину MN проведена прямая до пересечения с ВС в точке D. Найти длину AD.
Ответ: 
№5. Вершины В и С при основании равнобедренного треугольника АВС соеднены прямыми с серединой О его высоты., проведённой из вершины А. Эти прямые пересекают боковые стороны АС и АВ в точках D и Е соответственно. Найти площадь четырёхугольника АEOD, если площадь треугольник АВС равна S.
Ответ: 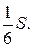
СПИСОК ЛИТЕРАТУРЫ
1. Барыбин К.С. Сборник геометрических задач на доказательство: пособие для учителей / К.С. Барыбин. – М.: Гос. учеб.-педаг. изд-во Мин. Просвещения РСФСР, 1954. – 154 с.
2. Великина П.Я. Сборник задач по геометрии для 6-8 кл.: пособие для учителей / П.Я. Великина – М.: Просвещение, 1971. – 207 с.
3. Габович И.Г. Алгоритмический подход к решению геометрических задач: книга для учителя / И.Г. Габович. – Киев: Радянська школа, 1989. – 160 с.
4. Геометрия: учебник для 7–9 кл. общеобразовательных учреждений / Л.С. Атанасян [и др.]. – М.: Просвещение, 2000. – 335 с.
5. Гусев В.А. Практикум по решению математических задач: Геометрия: учебное пособие для студентов физ.-мат. спец. пед. ин-тов / В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович. – М.: Просвещение, 1985. – 223 с.
6. Единый государственный экзамен 2006. Математика: учебно-тренировочные материалы для подготовки учащихся / Рособрнадзор, ИСОП. – М.: Интеллект-центр, 2006. – 272 с.
7. Киселёв А.П. Геометрия: Планиметрия: 7-9 кл.: учебник и задачник / А.П. Киселев, Н.А. Рыбкин. – М.: Дрофа, 1995. – 352 с.
8. Клово А.Г. Единственные реальные варианты заданий для подготовки к единому государственному экзамену. ЕГЭ – 2007. Математика / А.Г. Клово. – М.: Федеральный центр тестирования, 2007. – 94 с.
9. Погорелов А.В. Геометрия: учебник для 7 – 11 кл. общеобразоват. учреждений / А.В. Погорелов. – 10-е изд. – М.: Просвещение, 2000. – 383 с.
10. Полонский В.Б. Геометрия: задачник к школьному курсу / В.Б. Полонский, Е.М. Рабинович, М.С. Якир. – М.: АСТ-ПРЕСС: Магистр-S, 1998. – 252 с.
СОДЕРЖАНИЕ
Предисловие.......................................................3
I. Подобные треугольники........................................... 5
I.1. Теоретическая карта №1............................................5
I.2. Доказательство утверждений теоретической карты №1..................7
I.3. Задачи к теоретической карте №1...................................12
II. Пропорциональные отрезки.. ….................................. 24
II.1. Теоретическая карта №2..........................................24
II.2. Доказательство утверждений теоретической карты №2................25
II.3. Задачи к теоретической карте №2.................................. 27
III. Окружность.................................................... 34
III.1. Теоретическая карта №3......................................... 34
III.2. Доказательство утверждений теоретической карты №3............... 36
III.3. Задачи к теоретической карте №3................................. 38
IV. Биссектрисы углов треугольника.................................48
IV.1. Теоретическая карта №4.........................................48
IV.2. Доказательство утверждений теоретической карты №4...............49
IV.3. Задачи к теоретической карте №4................................. 52
V. Медианы треугольника...........................................60
V.1. Теоретическая карта №5.......................................... 60
V.2. Доказательство утверждений теоретической карты №5............... 61
V.3. Задачи к теоретической карте №5..................................65
VI. Треугольник и окружность.......................................73
VI.1. Теоретическая карта №6......................................... 73
VI.2. Доказательство утверждений теоретической карты №6............... 74
VI.3. Задачи к теоретической карте №6................................. 77
VII. Площадь треугольника......................................... 86
VII.1. Теоретическая карта №7.........................................86
VII.2. Доказательство утверждений теоретической карты №7...............87
VII.3. Задачи к теоретической карте №7.................................88
VIII. Четырехугольники............................................ 97
VIII.1. Теоретическая карта №8........................................97
VIII.2. Доказательство утверждений теоретической карты №8..............98
VIII.3. Задачи к теоретической карте №8...............................102
IX. Трапеция и параллелограмм.................................... 110
IX.1. Теоретическая карта №9....................................... 110
IX.2. Доказательство утверждений теоретической карты №9.............. 112
IX.3. Задачи к теоретической карте №9................................ 115
Х. Приложение................................................. 126
Список литературы...............................................130
Учебное издание
БОНДАРЕНКО Татьяна Евгеньевна, ПОТАПОВ Александр Сергеевич
ТЕОРЕТИЧЕСКИЕ КАРТЫ
И ЗАДАЧИ ПО ПЛАНИМЕТРИИ