Подбор размеров поперечных сечений стержней плоских рам.

Условие статической прочности,используемое для проектировочных расчетов прямых стержней рам при прямом плоском изгибе, при которых определяются требуемые значения характеристик и размеров расчетного сечения:Wx≥ , или Wx≥

Где -допускаемое нормальное напряжение(расчетное сопротивление) при изгибе материала, из которого изготовлен изгибаемый стержень.

-расчетный изгибающий момент в расчетном сечении рамы.

Затем по расчетному значению Wx в справочнике подбирают размер стандартного сечения.

Требуемый диаметр круглого сплошного сечения определяется по формуле: d≥

Требуемый наружный диаметр трубчатого сечения определяется по формуле: d≥

Основное условие статической прочности,используемое для проверочных расчетов прямых стержней рам при прямом плоском изгибе совместно с продольной силой: max Qu= ≤[Qu] или Ru

N-продольная сила,А-площадь сечения.

Касательное напряжение при деформации прямого плоского изгиба определяется по формуле Журавского: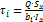

Максимальной касательное напряжение

-для прямоугольного сечения

max

-для круглого сечения max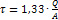

Проверочный расчет на статическую прочность по касательным напряжениям при прямом плоском изгибе:

43. Основные теории прочности деформируемых тел: общие положения

Введение критерия прочности позволяет заменить конкретное сложное НС простым одноосным растяжением или сжатием и установить при этом такое эквивалентное напряжение δ_эк одноосного растяжения-сжатия, которое равноценно по своему влиянию на величину критерия прочности. При этом используют гипотезу о преимущественном влиянии на прочность материала того или иного фактора: при любом НС нарушение прочности материала наступит тогда, когда величина данного фактора достигент предельного значения.

1-я теория прочности (теория Галилея, поддерживалась позднее Ламе, Рэнкиным и др. уч)- использует критерий наибольших нормальных напряжений.

По этой теории напряженные состояния считаются равнопрочными, если у них равны наибольшие нормальные напряжения.

Условия прочности по 1 – й теории прочности: δ_эк1=δ₁≤[δ] (при растяжении) или

δ_эк1=δ₃≤[δ_сж] (при сжатии)

2-теория прочности – критерий наибольших линейных деформаций.

Напряженные состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие по абсолютной величине линейные деформации ǀƐ_maxǀ.

Исходное условие прочности по 2 теории:

ǀƐ_maxǀ≤[Ɛ],

Где [Ɛ] – допускаемая линейная деформация стержня.

Для правой части используем закон Гука для одноосных деформаций [Ɛ]= δ/Е, для левой обобщенный закон Гука для пространственного НС.

Ɛ_max = Ɛ₁ =

Тогда условие прочности запишется в виде соотношения эквивалентного и допускаемых напряжений:

δ_эк2=δ₁-ʋ(δ₂ + δ₃) ≤[δ]

где ʋ - коэффициент поперечной деформации материала.

3-я теория прочности – использует критерий наибольших касательных напряжений.

Напряженные состояния равнопрочны по появлению недопустимых пластических деформаций, если у них равны наибольшие касательные напряжения.