Нормальное напряжение при внецентренном растяжении-сжатии элемента конструкции силой F в призвольной точке поперечного сечения i c координатами xi и yi определяется по принципу суперпозиций(простого сложения напряжений от отдельных силовых факторов):
σi= 
+ 
+ 
,
где Mx=F*yF- изгибающий момент от внецентренно приложенной внешней силы F относительно оси x на плече yF,
My=F*xF-изгибающий момент от внецентренно приложенной внешней силы F относительно оси y на плече xF,
N=F –внутренняя продольная сила в сечениях элемента конструкции;
xF, yF – координаты точки приложения внешней силы в системе главных осей инерции поперечного сечения элемента конструкции.
Для расчета таких стержней на прочность,особенно при произвольной (нисимметричной) форме их поперечного сечения,необходимо определить наиболее напряженные точки сечения,для чего,в свою очередь,следует предварительно определить положение нулевой линии(НЛ).Уравнение НЛ можно получить,приравняв нулю выражение нормального напряжения по последней формуле и обозначив N=F, Mx=F*yF и My=F*xF, Ix= 
*A и Iy= 
*A,а также xi=xн и yi=yн (где xн и yн - координаты какой –либо точки НЛ):
σi=σн= 
+ 
+ 
=0,откуда
1+ 
+ 
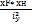=0.
Теперь с помощью последнего уравнения координаты двух точек нулевой линии (НЛ)при внецентренном растяжении-сжатии элемента конструкции определяется следующим образом:
-1-я точка НЛ-приняв xн=0,получим yн= - 
;
-2-я точка НЛ-приняв yн=0,получим xн= - 
,
где ix,iy- главные радиусы инерции поперечного сечения элемента конструкции.
По этим расчетным координатам двух точек можно для каждого конкретного сечения построить НЛ и определить положения наиболее напряженных точках сечения в растянутой и сжатой его областях.Следует отметить,что при внецентренном растяжении или сжатии НЛ может как пересекать сечение стержня,так и находиться за его пределами.Если НЛ пересекает сечение,то в нем есть зоны растяжения и сжатия.Если же НЛ не пересекает сечение,то напряжение во всех точках сечения будут одного знака.Если продольная сила F приложена вдоль центральной оси z сечения,то НЛ удалена в бесконечность и напряжения в этом случае по всему сечению распределены равномерно.
|
|
№35 Условия прочности стержней при внецентренном растяжении-сжатии стержней.(стр 48)
Условие статической прочности при внецентренном растяжении-сжатии элемента конструкции с произвольной формой поперечного сечения при проверочных расчетах записывается в традиционной форме сопоставления напряжений:
σmax= + + ≤Ru или [σu],
где x и y-координаты точки поперечного сечения,наиболее удаленной от нулевой линии (в сжатой либо растянутой зонах);
А-площадь расчетного поперечного сечения стержня;
Ix и Iy- осевые моменты инерции площади расчетного поперечного сечения стержня;
Ru или [σu]-расчетное сопротивление материала стержня при изгибе.
Вариант условия статической прочности при внецентренном растяжении-сжатии элемента конструкции с формами поперечного сечения,имеющими выраженные угловые точки(двутавр,прямоугольник,швеллер и др:
σmax= + 
+ 
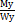≤Ru или [σu],
где Wx и Wy- осевые моменты сопротивления расчетных точек расчетного сечения стержня.
№36 Ядро сечения при внецентренном растяжении-сжатии стержней,его построение(стр 48 – 49)
НЛ может пересекать сечение,касаться его в точке или по линии,а также находиться полностью вне контура сечения.В окрестности центра тяжести С каждого сечения есть особая область,называемая ядром сечения.
|
|
Ядро сечения-область поперечного сечения стержня,которая характеризуется тем,что при приложении внешней продольной силы внутри или на границе этой области нормальные напряжения по всей площади сечения имеют один знак.Если силу F приложить на границе ядра сечения,то НЛ будет касаться контура сечения.
Одна из методик построения ядра сечения(ЯС) основывается на использовании ранее полученных формул,по которым определяются координаты двух точек НЛ при внецентренном растяжении-сжатии элемента конструкции.При этом для получения очертания ЯС рассматриваются все возможные положения касательных к контуру сечения и,принимая,что эти касательные являются нулевыми линиями,координаты граничных точек ЯС(xя=xF и yя=yF) вычисляются по формулам:
xя=xF=- 
; yя=yF=- 
.