ЭФФЕКТ ФАРАДЕЯ В ВЕЩЕСТВАХ С ИСКУССТВЕННОЙ ОПТИЧЕСКОЙ АКТИВНОСТЬЮ

 

В 1846 г. Фарадею удалось обнаружить эффект поворота плос­кости поляризации в изотропной среде, когда она помещалась в магнитное поле (и, следовательно, превращалась в оптически ак­тивное вещество). Оптическая схема установки Фарадея показана на рисунке 11.13.

Рисунок 11.13

 

При выключенном токе в катушке 1, монохроматическое излучение от источника 2 проходит через поляроид 3 и превращается в линейно-поляризованную волну 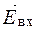. Пройдя через изотропную среду 4, излучение задерживается анализатором 5, поскольку его плоскость колебаний ортогональна плоскости колебаний поляризатора 3. 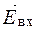Если на катушку 1 подать постоянное напряжение , в среде возникает магнитное поле , направленное вдоль вектора скорости волны, и вектор на выходе из среды оказывает­ся повёрнутым на угол относительно в плоскости орто­гональной вектору скорости волны 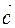. Для измерения угла , наблюдатель 6 должен повернуть анализатор на такой же угол для
полной ликвидации просветления поля зрения. Как было показано Фарадеем

 

, (11.33)

где 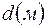- длина исследуемой среды,

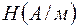- напряженность маг­нитного поля в среде,

- постоянная Верде (по имени ученого, занимавшегося, как и Фарадей, исследованием этого эффекта).

Природа эффекта Фарадея заключается во взаимодействии маг­нитных моментов валентных электронов диэлектрика с внешним магнит­ным полем напряженности . Под воздействием поля , разориентированные магнитные моменты 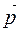изотропного диэлектрика стре­мятся сориентироваться либо в направлении , либо в направле­нии ему противоположном. Поле вектора увеличивает значения 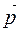, ориентирующиеся вдоль и ослабляет величины векторов 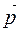, ориентированные в противоположном направлении. Увеличение 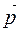приводит к возрастанию собственных частот колебаний ва­лентных электронов от до . 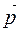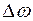Ослабление уменьшает на и 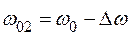. Увеличение собствен­ной частоты с до сдвигает кривую дисперсии 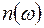вправо (рис. 11.14).

Рисунок 11.14

 

Уменьшение частоты до сдвигает кривую дисперсии влево. Для монохроматической волны длины 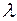, которой соответствует частота (рис. 11.14), абсолютный показатель преломления 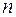становится равным 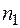, в соответствии с кривой дисперсии, сдви­нутой вправо, и принимает значение , в соответствии с кривой, сдвинутой влево. В результате оптическое излучение распадается на два потока, один из которых распространяется в диэлектрике с фазовой скоростью 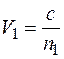, а другой - с . Как уже отмечалось для наблюдения эффекта Фарадея, излучение должно быть предварительно линейно-поляризованным.

Представляя линейно-поляризованную волну в виде суперпози­ции двух циркулярно-поляризованных по кругу волн (раздел 11.7) и пола­гая , , 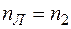, , получаем, что под воздействием магнитного поля изотропный диэлектрик ведёт себя подобно одноосному монокристаллу, оптическая ось которого сов­падает с линией вектора и вектор поляризованной вол­ны поворачивается на угол 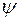, определяемый формулой (11.31).

Из приведённых рассуждений следует, что

 

~ .

 

Согласно (11.31),

 

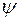~ при .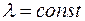

 

То есть, получаем формулу (11.33):

 

 

Закон малюса

 

Как следует из разделов 11.1 – 11.8, в ряде случаев необходимо знать соотношение между интенсивностью поляризованного света на входе
() в анализатор 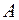(рис. 11.15) и интенсивностью на выходе из не­го .

Пусть угол между плоскостями колебаний вектора в поляриза­торе (Π) и анализаторе (А) равен (рис. 11.16).

Очевидно, что анализатор (А) пропустит лишь компоненту вектора , равную

 

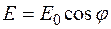. (11.34)

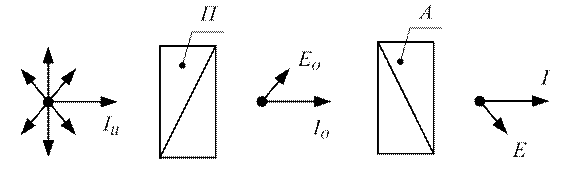
Рисунок 11.15

 

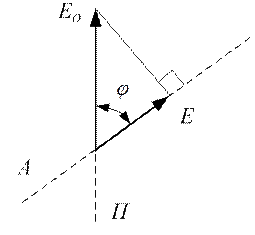
Рисунок 11.16

 

Интенсивность волны пропорциональна квадрату вектора напряженности (см. раздел 3.2):

 

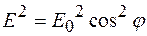~ , (11.35)

 

~ . (11.36)

 

Деля (11.35) на (11.36) почленно, получим,

 

, . (11.37)

 

Пусть 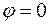, , 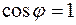и в идеальном анализаторе . В реальном анализаторе на величину ,.т.е.

 

, (11.38)

где - суммарные потери, связанные с поглощением и отраже­нием волны. Величина

 

(11.39)

 

называется коэффициентом относительных потерь. Согласно (11.39)

 

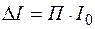(11.40)

 

Подставляя (11.40) в (11.38), получаем:

 

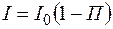. (11.41)

 

Величина имеет смысл коэффициента относительного про­пускания анализатора. Согласно (11.37) и (11.41) при произвольном уг­ле имеем:

 

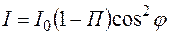. (11.42)

 

Формула (11.42) отражает сущность закона МАЛЮСА, согласно которому

.

 

 

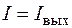
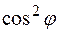КОНТРОЛЬНЫЕ ВОПРОСЫк главе 11

 

1. Чем отличается поляризованное оптическое излучение от неполяризованного?

2. В чем суть поляризации света как физического явления?

3. В чем суть двойного лучепреломления?

4. Понятие о главной оптической оси и главной плоскости монокристалла.

5. Возможно ли двойное лучепреломление в изотропных средах?

6. Какие способы получения циркулярно-поляризованного света Вам известны?

7. В чем сущность квадратичного электрооптического эффекта Керра?

8. Какие вещества называют оптически активными?

9. Как Вы понимаете искусственную оптическую активность вещества?

10. В чем суть магнитооптического эффекта Фарадея?

11. Суть закона Малюса.

12. Сделать вывод формул (11.5), (11.13), (11.21), (11.31), (11.32).

Глава 12. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ ОТ

УГЛА ВВОДА ИЗЛУЧЕНИЯ В ДИЭЛЕКТРИК

 

 

12.1. СЛУЧАЙ НОРМАЛЬНОГО ПАДЕНИЯ ВОЛНЫНА ГРАНИЦУ РАЗДЕЛА «СРЕДА-ДИЭЛЕКТРИК»

 

Направим электромагнитную волну

 

,

 

, (12.1)

 

из среды с показателем преломления на диэлектрик с показа­телем

преломления , рис. 12.1:

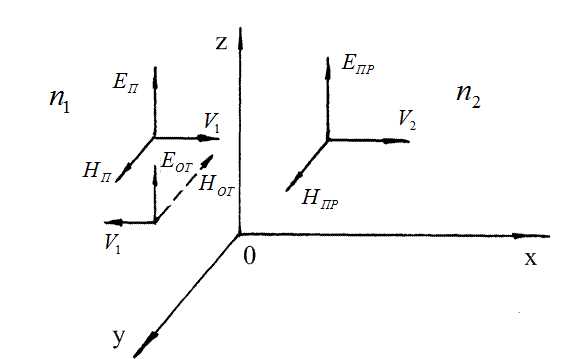
Рисунок 12.1

 

Плоскость диэлектрика совмещена с плоскостью 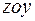декарто­вой системы координат, 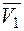- фазовая скорость монохроматичес­кой волны в среде, - скорость волны в диэлектрике. Пройдя границу раздела, в диэлектрике распространяется волна

 

,

 

, (12.2)

Отражается от границы раздела волна

 

,

 

. (12.3).

 

На границе раздела двух сред тангенциальная составляющая электри­ческого поля слева от границы ()равна тангенциальной сос­тавляющей справа от границы (),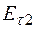

 

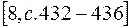
. (12.4)

 

Аналогично, 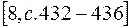, для магнитного поля

 

, (12.5)

 

Как видно из рис. 12.1,

 

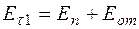, (12.6)

 

. (12.7)

 

Из (12.4), (12.6), (12.7) имеем:

 

. (12.8)

 

Подставляя в (12.8) значения 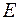из систем (12.1; 12.2; 12.3) и учитывая, что на границе раздела = 0, получаем (, ):

 

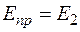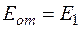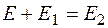. (12.9)

 

Аналогично, для магнитного поля:

 

,

 

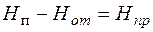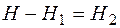. (12.10)

 

Известно, что амплитудные значения энергии электрического, и магнитного поля в электромагнитной волне одинаковы 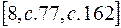. Следова­тельно, одинаковые и плотности амплитудных значений энергии:

 

,

 

Откуда

.

 

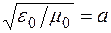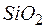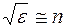Обозначив постоянную ; учитывая, что для стекловолокон из величина порядка 1, а , получаем взаимосвязь между амплитудами и 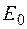в виде

 

, (12.11)

 

На основе (12.11) формула (12.10) преобразуется к виду:

 

 

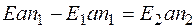
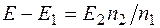. (12.12)

 

Складывая (12.9) и (12.12) почленно, получаем:

 

,

 

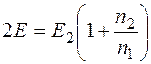. (12.13)

 

Подставляя (12.13) в (12.9), находим

 

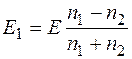. (12.14)

 

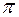Анализ формул (12.13) и (12.14) показывает, что при любом численном соотношении между и , фаза волны прошедшей через границу раздела та же, что и у падающей. Отраженная волна не изменяет фа­зу, если , и изменяет фазу на , если , (т.к. в этом случае дробь в формуле (12.14) меньше нуля). Пусть интенсивность падающей волны равна , отраженной - 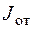. Поскольку интенсивность волны пропорциональна квадрату ее ампли­туды, а коэффициент отражения

, (12.15)

 

(12.16)

 

(12.17)

 

 

12.2. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ ВОЛНЫОТ УГЛА ПАДЕНИЯ, ПРИ ЛИНЕЙНОЙ ПОЛЯРИЗАЦИИ ВЕКТОРА 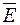В ПЛОСКОСТИ, ОРТОГОНАЛЬНОЙ ПЛОСКОСТИ ПАДЕНИЯ

 

Пусть волна падает на диэлектрик под углом 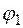, отра­жается под тем же углом и преломляется в диэлектрик под углом 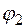(рис. 12.2).

 

Рисунок 12.2

 

Векторы , , имеют смысл амплитудных значений вблизи границы раздела и расположены в плоскости рисунка. Векторы 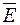, , 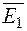поляризованы линейно в плоскости ортогональной плоскости рисунка, направлены за плоскость рисунка и обозначены символом .

Из рисунка 12.2 видно, что тангенциальная составляющая поля 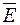в
первой среде, с показателем преломления :

 

,

 

а во второй среде, с абсолютным показателем преломления

 

.

 

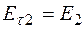Согласно (12.4),

 

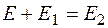. (12.18)

 

Из рис. 12.2 и формулы (12.5) следует, что

 

,

 

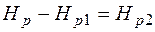где

,

 

откуда

. (12.19)

 

Согласно (12.11):

 

. (11.20).

 

Подставляя (12.20) в (12.19), получаем

 

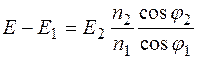. (12.21).

 

Согласно закона преломления,

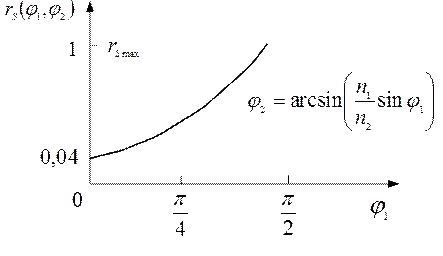
Рисунок 12.3

 

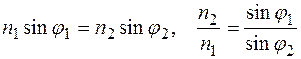. (12.22)

 

Из (12.21) и (12.22)

 

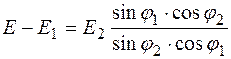. (12.23)

 

Разделим (12.18) на (12.23) почленно:

 

.

 

Освобождаясь от знаменателя, имеем:

 

 

. (12.24)

 

Согласно (12.24), коэффициент отражения волны, поляризованной в плоскости, ортогональной плоскости падения:

 

,

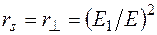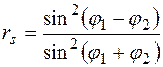. (12.25)

 

График функции показан на рис. 12.3.

 

 

12.3. ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА ОТРАЖЕНИЯ ВОЛНЫОТ УГЛА ПАДЕНИЯ, ПРИ ЛИНЕЙНОЙ ПОЛЯРИЗАЦИИ ВЕКТОРА 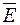В ПЛОСКОСТИ ПАДЕНИЯ

 

Если вектор напряженности электрического поля поляризован в плоскости падения, взаимное расположение амплитудных векторов вблизи границы раздела соответствует рис. 12.4, где символика обозна­чений та же, что и на рис. 12.2, за исключением того, что векторы направлены от плоскости чертежа (к нам), ().

Из уравнений (12.4, 12.5) и рис. 12.4 следует:

 

,

 

.

 

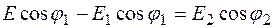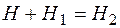Деля на и учитывая формулу (12.11), преобразуем систему к виду

 

,

 

.

 

Разделив уравнения почленно, получаем:

 

.

 

Откуда

 

,

 

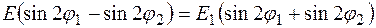. (12.26)

 

Рисунок 12.4

 

Известно, что

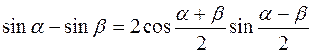, (12.27)

 

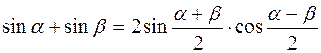. (12.28)

 

С учетом (12.27, 12.28), формула (12.26) принимает вид:

 

,

(12.29)

 

Согласно (12.29) коэффициент отражения волны, поляризованной в плос­кости падения

 

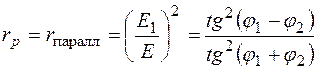, (12.30)

Рисунок 12.5

 

График функции 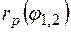, определяемой формулой (12.30), показан
на рис. 12.5.

 

 

12.4. закон брюстера как следствие из формулы Френеля для

 

Выражения (12.25) и (12.30) носят название формул Френеля. Как видно из графика рис. 12.5, функция 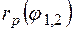=0, при некотором угле 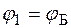. Этот угол можно найти из сле­дующих соображений.

Коэффициент отражения 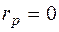, при условии, что в формуле (12.30). Следовательно, .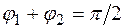

В этом случае угол

,

.

 

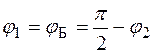Разделим последнее выражение на 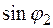, получим:

 

.

 

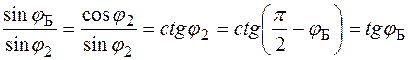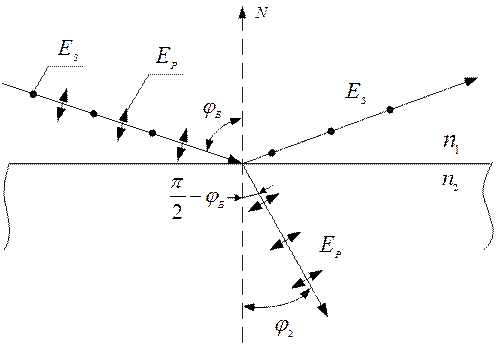
Рисунок 12.6

 

Но согласно закона Снеллиуса и рис. 12.6:

 

.

 

Следовательно,

. (12.31)

 

Таким образом, если волна, в которой вектор 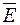поляризован в плоскос­ти падения от поверхности диэлектрика не отражается, она па­дает на него под углом

 

. (12.32)

 

Последнее утверждение носит название ЗАКОНА БРЮСТЕРА.

 

 

СЛЕДСТВИЕ 1 ИЗ ЗАКОНА БРЮСТЕРА

 

Если , волна полностью преломляется в диэлект­рик, при , и полностью отражается при .

СЛЕДСТВИЕ 2

 

Если на диэлектрик падает одновременно свет двух поляриза­ци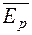й () и (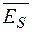), волны, отраженные под углом , полностью поляризованы в плоскости, ортогональной плоскости падения, а волны, преломленные в диэлектрик под углом 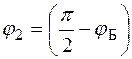,полностью поляризованы в плоскости падения (рис. 12.6).

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫК ГЛАВЕ 12

 

1. Понятие о коэффициенте отражения электромагнитной волны.

2. От чего зависит величина коэффициента отражения при нормаль­ном падении волны на диэлектрик?

3. Как взаимосвязаны коэффициент отражения с углом падения 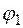и углом преломления 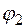, для волн, поляризованных в плоскости, ортогональной плоскости падения.

4. Сделать вывод формул (12.17), (12.25), (12.30).

5. Суть закона Брюстера и следствия из него.

6. Показать, что формула (12.32) является следствием из формулы (12.30)Френеля и закона преломления.