Глава 13. ВОЛНОВАЯ И ЛУЧЕВАЯ ПРИРОДА ЗАКОНОВ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА

ЗАКОНЫОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА КАК СЛЕДСТВИЕ СУПЕРПОЗИЦИИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ

Направим электромагнитную волну с волновым вектором вдоль радиуса вектора 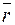трёхмерной декартовой системы коорди­нат (рис. 13.1). Ориентация векторов и 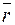определяется уг­лами между векторами и ортами совмещенными с осями 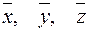системы координат. Взаимосвязь между век­торами и их проекциями имеет вид :

 

(13.1)

 

. (13.2)

 

Электрическая компонента волны, распространяющейся вдоль 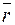имеет вид:

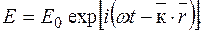. (13.3)

 

Согласно правилу скалярного произведения векторов, и формул (13.1), (13.2), величина

 

 

(13.4)

 

Учитывая, что и подставляя (13.4) в (13.3), получим

 

. (13.5)

 

где 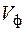- фазовая скорость монохроматической волны.

Потребуем, чтобы плоскость в которой распространяется све-­
товой луч, совпадала с плоскостью (рис 13.1). В этом случае и согласно (13.5),

Рисунок 13.1

 

 

Рисунок 13.2

Рисунок 13.3

Рисунок 13.4

 

. (13.6)

 

Пусть волна падает на границу раздела двух сред, которая совпадает с плоскостью .Ниже плоскости абсолют­
ный показатель преломления равен , а выше плоскости , показатель преломления равен , а

Для падающей волны на границе раздела (рис. 13.2), и уравнение (13.6) снова упрощается

 

. (13.7)

 

Отраженной от границы раздела волне соответствует уравнение

 

, (13.8)

 

поскольку , как и для падающей волны, рис. 13.3.

Преломляемой во вторую среду волне соответствует уравнение

 

, (13.9)

 

и рисунок 13.4.

На границе раздела тангенциальная составляющая электричес­кой компоненты поля над плоскостью должна быть равна аналогичной компоненте под плоскостью :

 

. (13.10)

 

Из (13.7), (13.8), (13.9) и (13.10) следует:

 

. (13.11).

 

Равенство (13.11) выполняется при выполнении следующих двух условий:

 

1) ,

 

2) . (13.12)

 

Из первого условия следует, что частоты отраженной () и преломленной () волн не отличаются от частоты волны (), падающей на границу раздела. Из второго условия выте­кают следующие важные следствия:

 

1)

 

т.е. отраженная и преломленная волна лежит в плоскости 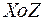, в одной плоскости с падающей волной.

В результате равенство (13.12) упрощается:

 

. (13.13)

2) Согласно (13.13), , , (рис. 13.4), т.е. угол падения равен углу отражения.

3) Поскольку должно выполняться условие то

 

 

(13.14)

 

Из рис. 13.4 следует, что

 

(13.15)

 

(13.16)

 

Подставляя (13.15) и (13.16) получаем закон преломления света из (13.14):

 

(13.17)

 

Полученные результаты позволяют сформулировать два фундаментальных закона лучевой оптики:

 

ЗАКОН ОТРАЖЕНИЯ СВЕТА

При падении монохроматической волны на границу раз­дела двух сред с различными абсолютными показателями преломления луч падающий и луч отражённый лежат в одной плоскости с нормалью к границе раздела двух сред. Угол отражения равен углу падения 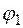и не зависит от соотношения между и . Частота отражённой волны равна частоте падающей волны.

 

ЗАКОН ПРЕЛОМЛЕНИЯ СВЕТА

При падении монохроматической волны на границу раздела двух сред с абсолютными показателями преломления и , из первой среды во вторую, луч падаю­щий и луч преломленный лежат в одной плоскости с нормалью к границе раздела двух сред. Угол падения 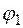и угол преломления 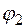связаны между собой соотношением:

 

 

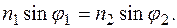
Частота преломленной волны не отличается от частоты падающей волны.