ЦИЛИНДРИЧЕСКИЙ ДИЭЛЕКТРИЧЕСКИЙ ВОЛНОВОД

КОНСТРУКЦИЯ ЦИЛИНДРИЧЕСКИХ ДИЭЛЕКТРИЧЕСКИХ ВОЛНОВОДОВ (СТЕКЛОВОЛОКОН) И РАСПРЕДЕЛЕНИЕ В НИХ ПРОФИЛЯ АБСОЛЮТНОГО ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ

Стекловолокно представляет собой стеклянный цилиндричес­кий стержень диаметра 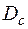с абсолютным показателем преломления , вокруг которого располагается симметричная цилиндричес­кая оболочка с наружным диаметром из стекла с абсолютным показателем преломления .

В стекловолокнах со ступенчатым профилем абсолютного пока­зателя преломления зависимость имеет характерное скачко­образное распределение (рис. 14.9).

В процессе изготовления стекловолокна, его центральная
часть и оболочка выращиваются (например, вытягиваются из распла­ва) как единое целое. Стекловолокно, изображенное на рис. 14.9,
граничит с воздухом, для которого . Стекловолокна, у
которых зависимость имеет плавное относительно оси симметрии стекловолокна распределение,получили название градиентных, рис. 14.10.

Как для ступенчатых, так и для градиентных стекловолокон, зависимость , практически остается постоянной для всей оболочки.

НОМИНАЛЬНАЯ ЧИСЛОВАЯ АПЕРТУРА СТЕКЛОВОЛОКНА

Направим узкий световой пучок на торец стекловолокна под углом к оси его симметрии в плоскости, проходящей через диаметр волокна, рис. 14.11. Плоскость торца полагаем ортого­нальной оси симметрии волокна.

Рисунок 14.9

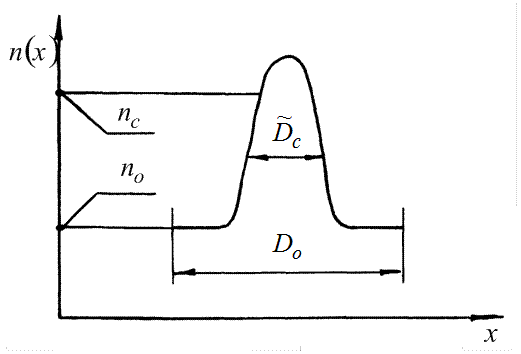
Рисунок 14.10

Рисунок 14.11

Пусть профиль в волокне является ступенчатым, а угол соответствует ПРЕДЕЛЬНОМУ значению угла (раздел 14.1). Найдём взаимосвязь угла падения луча на торец стекловолокна с пре­дельным углом . Из рис. 14.11 и закона преломления:

. (14.16)

Из :

. (14.17)

Подставим (14.17) в (14.16):

, (14.18)

. (14.19)

Согласно рис. 14.11 и закона преломления, в окрестности точки

,

,

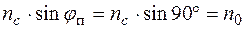. (14.20)

Складывая (14.19) и (14.20) почленно, имеем:

,

,

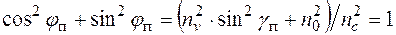. (14.21)

Величина (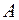) носит название номинальной числовой апертуры стекловолокна и является одной из его фундаментальных лучевых ха­рактеристик, поскольку определяется только значениями и . Угол называют апертурным углом.

Анализ формулы (14.21) показывает, что лучи лежащие внутри светового конуса с углом при вершине , рис. 14.12, способны испытывать полное внутреннее отражение от границы "центр-оболочка". Такие лучи концентрируются в процессе распространения в центральнойчасти волокна.

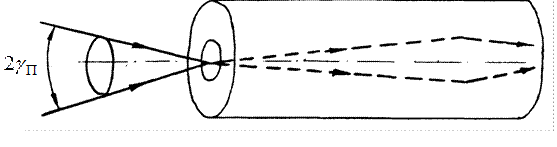
Рисунок 14.12

Лучи, выходящие за пределы указанного конуса не испытывают полного внутреннего отражения от границы "центр-оболочка", проникаютв оболочку и электромагнитная волна в стекловолокне быстро затухает.

Таким образом, одно из необходимых условий ввода излучения в стек­ловолокно по любой диаметральной плоскости, торцу волокна:

, (14.22)

где , согласно (14.21) определяется выражением

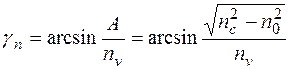. (14.23)

Формула (14.23) справедлива лишь для стекловолокон со ступенчатым распределением профиля . Если же 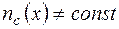, понятие апертурного угла перестает быть однозначным:

, (14.24)

где - два соседние пограничные значения внутри центральной час­ти градиентного волокна, аналогичные значениям и в волокнах со ступенчатым профилем.