Известно, что даже у наиболее совершенных газовых лазеров расходимость светового пучка достигает 10 
рад, а у твердотельных, используемых в ВОЛС, она на 1 
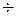2 порядка больше. Поэтому для получения волновых фронтов близких к плоским реальные световые пучки требуют дополнительной фокусировки с помощью объектива.
Пусть световой пучок, введенный в стекловолокно, является малорасходящимся, а ось его симметрии ортогональна торцу волокна и совпадает с осью симметрии волокна (рис. 14.14).
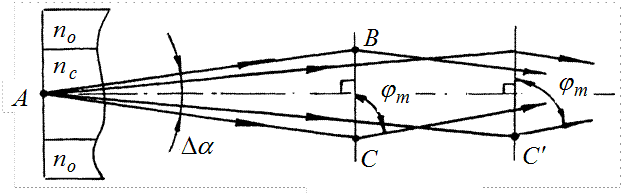
Рисунок 14.14
Рисунок 14.15
Волны, распространяющиеся внутри светового конуса 
, испытывают полное внутреннее отражение от границы “центр-оболочка” и согласно (14.15) взаимно не погашаются при целочисленных значениях параметра (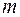
), входящего в формулу (14.15). При малой расходимости светового конуса 
, различие между 
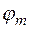в точке 
и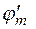 
в точке 
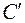невелико, следовательно число значений параметра (
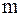) в данном случае ОГРАНИЧЕНО. При 
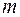(рис. 14.14), величина () обычно не выходит за пределы значений (0;I).
Если световой пучок вводится под некоторым углом к оси симметрии волокна, рис. 14.15, общее число значений возможных углов 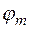возрастает, а их величина убывает. Следовательно, увеличивается число значений параметра 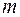= 0, I, 2, 3,....
Это приводит к увеличению возможных интерференционных условий, определяемых формулой (14.15) и интенсивность излучения на выходе волокна, при уменьшении угла 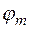, начинает возрастать.
Дальнейшее уменьшение углов 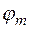переводит часть энергии волны в оболочку, т.к. углы 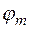становятся меньше предельного (раздел 14.1). Интенсивность излучения на выходе волокна в этом случае начинает убывать. Заметим, что уменьшению угла 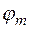соответствует увеличение угла 
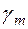(рис. 14.11).
Если 
, интенсивность излучения на выходе волокна соответствует некоторому значению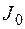 
, а геометрия хода лучей соответствует рис. 14.14. При увеличении угла 
от 0 до 
(рис. 14.11), интенсивность излучения возрастает от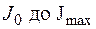 
. Если увеличивается от 
до больших значений, часть энергии волны переводится в оболочку и интенсивность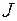 
убывает. Зависимость 
показана на рис. 14.16.
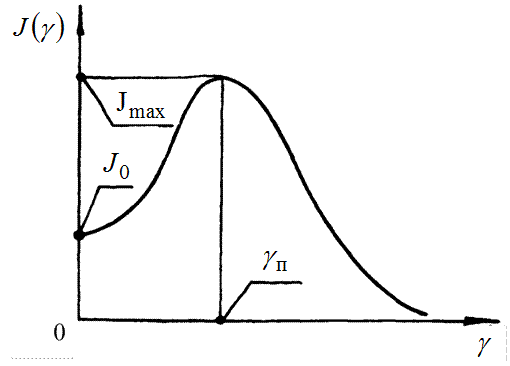
Рисунок 14.16
Экспериментальное исследование зависимости позволяет найти опытным путем значение 
и соответствующую ему величину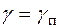 
, однозначно определяющую номинальную числовую апертуру 
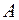согласно (14.21).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Понятие предельного угла и полного внутреннего отражения.
2. Конструкция пленарного волновода.
3. Вывод формулы (14.15) и её анализ.
4. Суть эффекта Гуса-Хенхена.
5. Распределение профиля абсолютного показателя преломления в ступенчатых и градиентных стекловолокнах.
6. Номинальная числовая апертура стекловолокна.
7. Вывод формулы (14.21) и её анализ.
8. Физическая природа дискретности углов ввода излучения в стекловолокно.
9. Обоснуйте ход зависимости , показанной на рис. 14.16.
Глава 15. УШИРЕНИЕ ИМПУЛЬСНЫХ СИГНАЛОВ В ПРОЦЕССЕ ИХ РАСПРОСТРАНЕНИЯ ПО СТЕКЛОВОЛОКНУ
Введение
В процессе распространения импульса света по стекловолокну его искажения обусловлены двумя основными причинами: увеличением длительности (уширением импульса во времени) и уменьшением амплитуды 
. В настоящем разделе рассматриваются основные физические причины, вызывающие уширение импульса.