ТЕЛЕСНЫЙ УГОЛ, СВЕТОВОЙ ПОТОК И МЕХАНИЧЕСКИЙ ЭКВИВАЛЕНТ СВЕТА

 

Рассмотрим точечный источник света , испускающий
свет равномерно во всё трёхмерное пространство (рис.17.2). Выберем в указанном пространстве световой конус с углом в его вершине, совпадающей с источником света . Пересечем световой конус сферической поверхностью радиуса . Как видно из рис. 17.2, конус «вырезает» на сферической поверхности площадку площади . Рассмотренный световой конус принято характеризовать величиной телесного угла 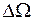, которая определяется как

 

, (17.2)

 

и измеряется в СТЕРАДИАНАХ (ср). Очевидно, что телесному углу в
1 ср соответствует условие . "Полному" телесному
углу, при котором точечный источник 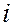излучает свет в сферу
радиуса соответствует величина и величина

 

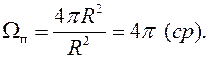(17.3)

 

Рисунок 17.2

 

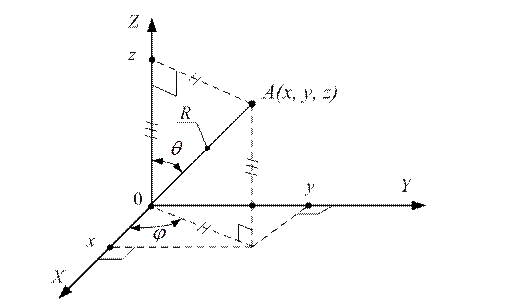
Рисунок 17.3

Рисунок 17.4

Рисунок 17.5

 

Найдем взаимосвязь величины телесного угла 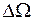с его ориентацией в пространстве.

Наряду с декартовой системой координат для опи­сания пространства часто используется сферическая система , где координата точки " 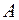" задаётся с помощью линейного отрезка , расположенного под углом к оси и угла между осью 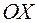и проекцией отрезка на плоскость (рис. 17.3).

 

Элементарный объем в декартовой системе координат

 

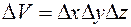. (17.4)

 

Найдем величину элементарного объема в сферической системе координат , рис. 17.5:

 

Согласно рис. 17.5, координата точки “ ” задана через параметры .Увеличим угол на . Очевидно, что

 

(17.5)

 

где - малый угол, измеряемый в радиа­нах;

 

Рисунок 17.6

 

 

 

 

Рисунок 17.7

 

,

 

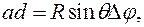(17.6)

 

Площадь фигуры и согласно (17.5) и (17.6), определяется выражением:

 

. (17.7)

 

Увеличим на (рис. 17.6).

Согласно рис. 17.6, величина элементарного объема в сферической системе координат

 

(17.8)

 

и является его эквивалентом в декартовой системе, формула (17.4).

Внесём конус с углом при вершине в систему , совмещенную со сферической системой координат , распо­ложив вершину конуса в центре системы координат, рис. 17.7.

Пересечем конус двумя сферическими поверхностями радиусов и . Элементарный объем пространства между ними

 

, (17.9)

 

где - площадь сферического сегмента в сечении . По­лагая достаточно малым, мы аппроксимируем фигуру . прямым круговым цилиндром, где - его высота, - пло­щадь основания. Потребуем, чтобы оба объёма, определяемые формулами (17.8) и (17.9) имели одинаковую величину:

 

, (17.10)

 

откуда:

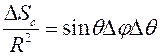, (17.11)

 

согласно (17.2) и (17.11):

 

, (17.12)

 

 

Рисунок 17.8

 

Переходя к бесконечно малым величинам, получаем взаимосвязь величины телесного угла с его параметрами и ориентацией в пространстве:

 

, (17.13)

 

Пусть монохроматическое излучение с длиной волны = 555 нм переносит через пло­щадку 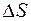(рис. 17.2) за 1с энергию 0,0016 Дж. Полагают, что в данном случае внутри телесного угла 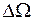распространяется световой поток , равный 1 люмену (лм).

 

Указанное соотношение является международным стандартом для 1 люмена.

Таким образом,

 

0,0016 = 0,0016 Вт ~ 1лм, (17.14)

 

при = 555 нм.

Пропорциональность (17.14) является не только определением 1 люмена, но и единственным связующим звеном между фотометрическими и энергетическими характеристиками оптического излучения.

 

Величину

 

принято называть механическим эквивалентом света . При = 1 лм, величина 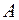численно равна

 

. (17.15)

 

Относительная функция видности (17.1), (рис. 17.1, табл. 17.1) и (17.15) позволяют рассчитать необходимую мощность излучения , соответствующую световому потоку в 1 лм для любой длины волны из диапазона

 

.

 

по формуле:

, Вт (17.16)

 

Например, пользуясь таблицей 17.1, находим, что световому потоку в 1 лм, при длине волны 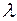= 633 нм, соответствует значение: = 0,25.

Согласно (17.6), для обеспечения такого светового потока необхо­дима мощность

 

,

 

Пусть гелий-неоновый лазер обладает мощностью излучения = 5· 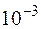Вт. Очевидно, что световой поток, соответствующий ему, определится из следующих зависимостей:

 

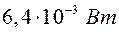~ 1 лм,

~ Ф лм,

 

которым соответствует пропорция:

 

откуда Ф = 0,78 лм.

 

СИЛА СВЕТА

Пусть внутри телесного угла 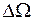распространяется световой поток (рис. 17.2).

 

Величина

 

, (17.17)

 

носит название СИЛЫСВЕТА источника .

 

Единица измерения силы света 1 кандела (кд) в настоящее время принята за основную фотометрическую (светомеханическую) единицу системы «SI».

 

Кандела равна силе света в заданном направ­лении, излучаемого монохроматическим источником с частотой 5,4·Ι0¹⁴ Гц, излучение которого в указанном направлении составляет 1/683(Вт/ср) .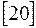

 

Заметим, что при силе света в 1 кд, световой поток, распространяющийся в телесном угле в 1 ср, равен 1 лм.

Действительно, согласно (17.17):

 

.