При решении задач из этой темы нужно использовать графический метод решения задач линейного программирования [1, гл. I, § 3, с. 27-37; 2, гл. 2, п. 2.2, с. 36-42].
Пример 1.1: Геометрическая интерпретация задачи линейного программирования.
В отделе технического контроля (ОТК) некоторой фирмы работают контролеры первого и второго разрядов. Норма выработки ОТК за восьмичасовой рабочий день составляет не менее 1800 изделий. Контролер первого разряда (К1) проверяет 25 изделий в час, причем не ошибается в 98 % случаев. Контролер второго разряда (К2) проверяет 15 изделий в час, его точность – 95 %.
Зарплата К1 – 4 доллара в час, К2 – 3 доллара в час. При каждой ошибке контролера фирма несет убыток в размере двух долларов. Фирма может использовать 8 К1 и 10 К2. Фирма хочет определить оптимальный состав ОТК, при котором общие затраты на контроль будут минимальны.
Разработка модели.
Пусть 
и 
обозначают количество контролёров К1 и К2 соответственно.
Число контролеров каждого разряда ограничено, т. е. имеются следующие ограничения:
(разряд 1),
(разряд 2).
Ежедневно необходимо проверять не менее 1800 изделий. Поэтому должно выполняться неравенство:
, или 
.
При построении целевой функции следует иметь в виду, что расходы фирмы, связанные с контролем, включают две составляющие: зарплату контролеров и убытки, вызванные ошибками контролеров.
Расходы на одного контролера К1 составляют:
4$ + 2 · 25 · 0,02 = 5 $/час.
Расходы на одного контролера К2 равны:
3$ + 2 · 15 · 0,05 = 4,5 $/час.
Следовательно, целевая функция, выражающая ежедневные расходы на контроль, имеет вид:
.
Задача линейного программирования:
Решение.
а) Область допустимых решений (ОДР) построим следующим образом. Построим прямые с уравнениями (см. рис. 1.1)
б) Каждое неравенство (1)-(5) определяет полуплоскость, причем эта полуплоскость, содержит бесчисленное множество точек, координаты которых удовлетворяют соответствующему строгому неравенству.
Легко видеть, что координаты точки 
удовлетворяют неравенствам (1) и (2). Поэтому две полуплоскости содержат начало координат системы 
.
Все допустимые решения лежат в первом квадранте, так как 
.
В силу ограничения все допустимые решения 
располагаются по одну сторону от прямой 
и на самой прямой. Нужную полуплоскость можно найти, проверив, например, удовлетворяет ли начало координат неравенству ; если нет, то подставляем в неравенство координаты любой точки, расположенной по другую сторону от прямой . Нужная полуплоскость отмечается штриховкой.
Для изображения ОДР следует начертить графики всех ограничений.
Рис. 1.1
Множеством решений системы неравенств (1)-(5) является пересечение множеств решений каждого из неравенств, входящих в систему. Штриховкой выделим ОДР – треугольник 
.
в) Строим нормальный вектор целевой функции 
. Подчеркнем, что его направление указывает на направление возрастания целевой функции 
.
Если зафиксировать значение целевой функции 
, то соответствующие точки будут лежать на некоторой прямой, перпендикулярной нормальному вектору . При изменении величины 
, прямая подвергается параллельному переносу. Рассмотрим прямые, соответствующие различным значениям , имеющие с ОДР хотя бы одну общую точку (на рис. 1.1 штриховые прямые).
Положим, 
. Прямая 
пересекает оси координат в точках 
и 
. При передвижении прямой в направлении вектора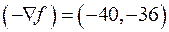 
(на рис. 1.1 направление движения указано стрелками) значение 
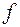уменьшается. Ясно, что для прямой, проходящей через угловую точку 
, дальнейшее движение невозможно. Следовательно, 
– оптимальное решение (план) и 
– минимальное значение целевой функции.
Таким образом, при оптимальном режиме работы ОТК необходимо использовать 8 контролеров первого разряда и 
контролеров второго разряда.
Дробное значение 
соответствует использованию одного из двух контролеров второго разряда в течение неполного рабочего дня. При недопустимости неполной нагрузки контролеров дробное значение обычно округляют, получая приблизительное оптимальное целочисленное решение: 
.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ№ 1
Решить графическим методом
|
Решить графическим методом
|
Решить графическим методом
|
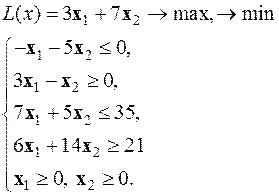
Решить графическим методом
|
Решить графическим методом
|
Решить графическим методом
|
Решить графическим методом
|
Решить графическим методом
|
Решить графическим методом
|
Решить графическим методом:
|
Пример 1.2: Симплекс-метод: основная схема алгоритма. Экономическая интерпретация итоговой симплекс-таблицы.
При решении задач из этой темы нужно изучить симплексный метод решения задач линейного программирования [1, гл. I, § 4, с. 45-58; 2, гл. 3, п. 3.1-п. 3.2, с. 95-117].