Своё название (simple (лат) – простой) этот метод получил от ограничения, входящих в одну из первых задач, решенных указанным методом.
Данное ограничение имеет вид
|
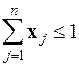
и представляет собой выпуклый многогранник в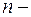 
мерном пространстве с вершинами на осях координат в точках
|
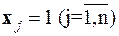
Впервые СМ был предложен американским ученым Дж. Данцигом в 1949 г., однако идеи СМ были разработаны еще 1939 г. российским ученым Л.В. Канторовичем.
Рассмотрим общую задачу линейного программирования с m ограничениями и n переменными, записанную в стандартной (канонической) форме:
| (1.1) |
при ограничениях:
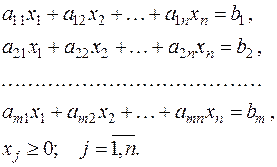
| (1.2) |
Как правило, число уравнений задачи меньше числа переменных (т.е.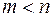 
), поэтому множество ее допустимых решений бесконечно. Следовательно, выбор наилучшего допустимого решения, минимизирующего ЦФ 
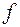(x), нетривиален.
Известен классический метод решения систем линейных уравнений – метод Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками. При использовании первых m переменных 
такая система имеет следующий вид:
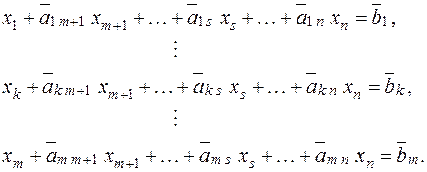
| (1.3) |
Или последние уравнения можно переписать следующим образом:
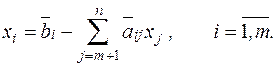
| (1.4) |
Переменные 
, входящие с единичными коэффициентами только в одно уравнение системы (1.4) с нулевыми – в остальные, называются базисными или зависимыми.
В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Остальные 
переменных 
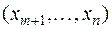называются небазисными или независимыми переменными.
При записи системы в каноническом виде все ее решения можно получить, присваивая независимым переменным произвольные значения и решая затем получающуюся систему относительно зависимых переменных. Для приведения системы к каноническому виду можно использовать 2 типа элементарных операций над строками:
|
|
- умножение любого уравнения системы на положительное или отрицательное число;
- прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число.
Базисным решением системы (1.4) называется решение, полученное при нулевых значениях небазисных переменных.
Например: в системе (1.4) одно из базисных решений задается как:
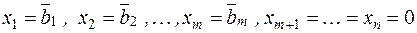
| (1.5) |
Определение допустимого (невырожденного) базисного решения.
Базисное решение называется допустимым (невырожденным) базисным решением, если значения входящих в него базисных переменных
,
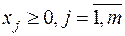что эквивалентно условию неотрицательности
.
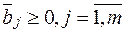Допустимое базисное решение является угловой точкой допустимого множества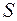 
задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел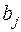 
в (1.4) есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.
Так как различные базисные решения (1.5)системы (1.4) соответствуют различным вариантам выбора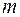 
переменных из общего числа 
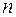переменных 
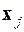, то число допустимых базисных решений (угловых точек) не превышает
.
Поэтому ЗЛП можно решать посредством перебора конечного числа угловых точек допустимого множества 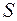, сравнивая значения целевой функции в этих точках – метод сканирования.
|
|
Пример: Если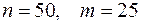 
, то 
(задача небольшой размерности), то ЭВМ, выполняя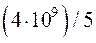 
переборов вариантов в 1 секунду, будет искать решение более 40 часов.
Идея СМ состоит в направленном переборе угловых точек допустимого множества 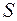с последовательным уменьшением (увеличением) целевой функции 
.
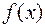Наиболее простой метод, используемый для решения ЗЛП, - это симплексный метод Данцига.
Здесь начало координат переносится в угловую точку допустимой области, и рассматриваются линии, соединяющие эту угловую точку со смежными угловыми точками. Исследуется вариация целевой функции 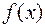вдоль этих линий, и если какая-нибудь из них дает улучшение, начало координат переносится в угловую точку, в которую ведется линия. Процесс затем повторяется для новой угловой точки и прекращается, когда достигается угловая точка, где 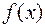не увеличивается (не уменьшается) вдоль любой такой линии.