| (1.6) (1.7) |
Решение.
Задача задана в канонической форме. Заполняем первый блок таблицы Гаусса и приступаем к поиску первого базисного допустимого решения.
1)
| 
| 
| 
| 
| Св. чл. | 
|
| -1 | -3 | |||||
| -1 | -1 | |||||
| -8 | 3:1 | |||||
| -1 | -3 | -7 | 
|
2)
|
|
|
|
|
| Св. чл. |
|
| -11 | ||||||
| -1 | -1 | 4:4 | ||||
| -8 | ||||||
| -5 | -4 | 
|
3)
|
|
|
|
|
| Св. чл. |
|
| -3/4 | 9/4 | 18:3 | ||||
| -1/4 | -1/4 | |||||
| -1 | 11:1 | |||||
| 1/4 | -19/4 | -4 |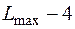 
|
4)
|
|
|
|
|
| Св. чл. |
|
| -1/4 | 3/4 | |||||
| -1/4 | -1/4 | |||||
| -3/4 | 5/4 | |||||
| -3/4 | -7/4 | 
|
Пояснения:
- первый разрешающий коэффициент взяли в первом столбце, т.к. он наиболее простой, в нем имеется один нуль;
- во второй таблице в качестве разрешающего взяли столбец с положительными коэффициентами индексной строки;
- в 3-й таблице в качестве разрешающего переменного можно взять или , хотя взять нужно , поскольку при коэффициент индексной строки положителен.
С другой стороны, взять нельзя, потому, что все коэффициенты этого столбца отрицательные – это приведёт к недопустимому решению. Поэтому в базис ввели .
Получено первое допустимое базисное решение.
Оно оптимально, т.к. в индексной строке нет положительных коэффициентов.
Замечание: При вычислении 
, отрицательные значения и нули не участвуют.
Оптимальное решение 
получено.
Подставляя полученное решение в (1.6), получим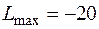 
.
Ответ: ,
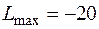
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ№ 1
0. Решить симплекс-методом ЗЛП:
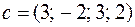
| 1. Решить симплекс-методом ЗЛП:
|
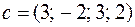
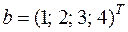
2. Решить симплекс-методом ЗЛП:
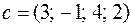
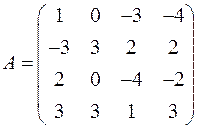
| 3. Решить симплекс-методом ЗЛП:
|
|
|
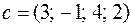
4. Решить симплекс-методом ЗЛП:
| 5. Решить симплекс-методом ЗЛП:
|
6. Решить симплекс-методом ЗЛП:
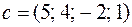
| 7. Решить симплекс-методом ЗЛП:
|
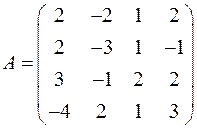
8. Решить симплекс-методом ЗЛП:
| 9. Решить симплекс-методом ЗЛП:
|
Решение задач линейного программирования (ЗЛП) в MS Excel
Цель работы: изучение порядка работы с электронной таблицей при решении задач оптимизации
Исходные положения. Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Часто математической моделью таких задач является задача линейного программирования.
Пример решения ЗЛП.
Задание.
Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и, после соответствующей обработки, поступают в продажу. Хотя недельный расход корма для цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт. Для того чтобы цыплята достигли к восьмой неделе необходимой весовой кондиции, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов. В качестве ингредиентов рассмотрим три: известняк, зерно и соевые бобы. Требования к питательности рациона сформулируем, учитывая три вида питательных веществ: кальций, белок и клетчатку. В таблице приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Заметим, что известняк не содержит ни белка, ни клетчатки.
|
|
| Ингредиент | Содержание питательных веществ, фунт/(фунт ингредиента) | Стоимость, долл./фунт | ||
| кальций | белок | клетчатка | ||
| Известняк | 0,38 | - | - | 0,04 |
| Зерно | 0,001 | 0,09 | 0,02 | 0,15 |
| Соевые бобы | 0,002 | 0,50 | 0,08 | 0,40 |
Смесь должна содержать не менее 0,8, но не более 1,2% кальция; не менее 22% белка; не более 5% клетчатки.
Требуется составить для птицеводческой фермы модель количества (в фунтах) каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Решение
Обозначим:
х1 – количество известняка в рационе; х2 – количество белка в рационе; х3 – количество клетчатки в рационе;
Рацион будет включать:
(0,38 х1+0,001 х2+0,002 х3) единиц кальция, (0,09 х2+0,5 х3) единиц белка и (0,02 х2+0,08 х3) единиц клетчатки.
Так как на содержание питательных веществ приведены соответствующие нормы, то получим систему неравенств:
0,38 х1+0,001 х2+0,002 х3 ≤ 0,012; (1.8)
0,38 х1+0,001 х2+0,002 х3 ≥0,008;
0,09 х2+0,5 х3 ≥ 0,22;
0,02 х2+0,08 х3 ≤ 0,05.
Кроме того, переменные
х1 >= 0, х2 >= 0, х3 >= 0. (1.9)
Общая стоимость рациона 1 цыплёнка составит (в $)
L(Х) = 0,04 х1+0,15 х2+0,40 х3. (1.10)
Итак, оптимизационная модель задачи:
L(Х) = 0,04 х1+0,15 х2+0,40 х3.→ min, (1.11)
0,38 х1+0,001 х2+0,002 х3 ≤ 0,012;
0,38 х1+0,001 х2+0,002 х3 ≥ 0,008; (1.12)
0,09 х2+0,5 х3 ≥ 0,22;
0,02 х2+0,08 х3 ≤ 0,05;
|
|
х1 >= 0, х2 >= 0, х3 >= 0, (1.13)
где Х = (х1, х2, х3).
Задачу (1.11) линейного программирования, например, можно записать таким образом:
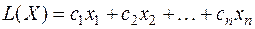(1.14)
при ограничениях:
(1.15)
. (1.16)
Здесь:
n= 
– число переменных;
m=4 – число ограничений;
- действительная матрица ограничений размерностью 
;
- коэффициенты при переменных в ограничениях (6);
– вектор–строка, 
– коэффициенты при переменных в целевой функции (5);
– вектор правой части ограничений;
- целевая функция.
Решение задачи линейного программирования в среде EXCEL.
Заполните таблицу исходных данных (1.11), (1.12), приведенную на листе Исходные данные;
В ячейках: B2:D2 вводятся начальные значения переменных;
Создайте копию листа Исходные данные и присвойте копии имя - Решение задачи.
Добавьте в ячейки на листе Решение задачи; текст и формулы в соответствии с таблицей.
| Имя ячейки | Формулы и текст |
| E8 | 
|
| F8 | bi |
| B9 | =B4*$B$2 |
| C9 | =C4*$C$2 |
| D9 | =D4*$D$2 |
| E9 | =СУММ(B9:D9) |
| B10 | =B5*$B$2 |
| C10 | =C5*$C$2 |
| D10 | =D5*$D$2 |
| E10 | =СУММ(B10:D10) |
| B11 | =B6*$B$2 |
| C11 | =C6*$C$2 |
| D11 | =D6*$D$2 |
| E11 | =СУММ(B11:D11) |
| B12 | =B7*$B$2 |
| C12 | =C7*$C$2 |
| D12 | =D7*$D$2 |
| E12 | =СУММ(B12:D12) |
| A14 | 
|
| B14 | =B2*B3+C2*C3+D2*D3 |
Щёлкните левой кнопкой мыши (ЩЛКМ) по яч.B14.
В меню Сервис выберете (ЩЛКМ) подпункт Поиск решения (см. рис. 1.2).
Если в меню Сервис подпункт Поиск решения (см. рис. 1.3) отсутствует, то выполните цепочку команд Сервис → Надстройки. В окне Доступные надстройки поставьте флажок напротив поля Поиск решения.
Рис.1.3.
В появившемся окне (см. рис. 1.4),
Рис.1.4.
заполнить соответствующие поля (ЩЛКМ) по маркеру 
и указывая (ЩЛКМ) имена ячеек.
Поле Ограничения заполняется (ЩЛКМ) по кнопке Добавить.
В появившемся окне
(ЩЛКМ) заполните соответствующие поля: Ссылка на ячейку: Ограничение: и выберите знак отношения (<= или =>, или =).
(ЩЛКМ) по кнопке Добавить;
После ввода последнего ограничения (ЩЛКМ) по кнопке ОК!!;
В окне Поиск решения (см. рис. 1.4) (ЩЛКМ) по кнопке Выполнить.
Выводы.
Итак, получено оптимальное решение: Смесь должна содержать 0,0187 фунта кальция и 0,44 фунта соевых бобов. Кормить зерном цыплят слишком расточительно.
Минимальная цена рациона 1 цыплёнка сост. $ 0,177.
Ограничения все выполнены.