При решении задач из этой темы необходимо ознакомиться с методами решения транспортной задачи [1, гл. 2, § 6 - §7, с. 85-110; 2, гл. 5, п. 5.1 – п. 5.5, с. 193-238].
ТРАНСПОРТНАЯ ЗАДАЧА
Основные понятия
Пусть имеются m производителей и известны объемы запасов по каждому производителю: а 1, а 2,..., а m. Известна потребность в грузах b 1, b 2,..., b n каждого из n пунктов назначения. Задана матрица транспортных издержек от каждого производителя к каждому потребителю: 
. Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза 
должно быть отправлено из каждого i – го пункта отправления в каждый j – й пункт назначения c минимальными транспортными издержками. Данные записываются в следующую таблицу:
Таблица 1. Общий вид транспортной таблицы.
| В1 | В2 | … | Вn | Запасы | |
| А1 | x11 c11 | x12 c12 | … | x1n c1n | а1 |
| А2 | x21 c21 | x22 c22 | … | x2n c2n | а2 |
| … | … | … | … | … | … |
| Аm | xm1 cm1 | xm2 cm2 | … | xmn cmn | аm |
| Потребности | b1 | b2 | … | bn |
Определение. Транспортная задача (ТЗ) называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения. Если такого равенства нет, то задачу называют открытой.
Суть этого определения в следующем: все потребности могут быть удовлетворены за счет запасов, и наоборот: все запасы разойдутся по потребителям без остатка. А значит, не требуются ни дополнительных поставщиков, ни дополнительных потребителей; не будет издержек, не будет дефицита.
Теорема 1. Для того чтобы ТЗ имела допустимые решения, необходимо и достаточно выполнения условия закрытости задачи.
Таким образом, если исходная ТЗ является открытой, необходимо преобразовать ее так, чтобы она стала закрытой. Правило преобразования будет описано далее в замечании.
Для написания модели необходимо записать следующие условия:
- все грузы из i - х пунктов должны быть отправлены:
.
- все j- е пункты потребления должны быть обеспечены грузами в полном объеме:
.
Суммарные объемы отправления должны равняться суммарным объемам назначения: 
Должно выполняться условие неотрицательности переменных.
Перевозки необходимо осуществить с минимальными транспортными издержками:
Z = 
® min.
Замечание.
Так как условие баланса суммарных поставок и потребностей является обязательным, то необходимо открытую задачу перевести в закрытую задачу по следующим правилам:
Если потребности превышают запасы, то вводится фиктивный поставщик с недостающим объемом отправления
Если запасы превышают потребности, то вводится фиктивный потребитель с недостающим объемом потребления.
Стоимость обслуживания транспортных потоков от фиктивных пунктов к реальным пунктам равна нулю.
Особенности транспортной задачи:
- распределению подлежат только однородные ресурсы,
- условия задачи описываются только уравнениями,
- все переменные выражаются в одинаковых единицах измерения,
- во всех уравнениях коэффициенты при неизвестных равны 1,
- каждая неизвестная встречается только в двух уравнениях системы ограничений.
Метод потенциалов
Так как транспортная задача является подвидом ЗЛП, то ее можно решать с помощью симплекс-метода, однако из-за специфичности формулировки можно применить более экономные методы. Наиболее распространенным методом решения транспортных задач является метод потенциалов.
Рассмотрим алгоритм метода потенциалов.
1. Разработка начального плана перевозок. Его еще называют начальным опорным решением;
2. Расчет потенциалов;
3. Проверка плана перевозок на оптимальность;
Если план не оптимальный, то ищут максимальное звено неоптимальности, то есть такого маршрута, где затраты на перевозку самые маленькие.
4. Составляют контур перераспределения ресурсов;
5. Определение минимального элемента в контуре перераспределения и перераспределение ресурсов по контуру, то есть переносят потоки с дорогих путей на более дешевые пути;
6. Получение нового плана перевозок;
7. Возвращаются к пункту 2.
Рассмотрим приведенный алгоритм более подробно.
Для разработки начального плана существует несколько методов:
- метод северо-западного угла;
- метод наименьших расходов;
- метод двойного предпочтения.
Рассмотрим метод наименьших расходов на конкретной модели.
Суть этого метода в том, что перевозки осуществляются в первую очередь по тем направлениям, где стоимость меньше. После того, как отправлены грузы по самым дешевым путям, начинают отправлять по более дорогим; и так далее, пока не истратятся все запасы, и не удовлетворятся все потребности.
Задача. В трех хранилищах 
имеется соответственно 
, 
, и 
тонн топлива. Требуется спланировать перевозку топлива четырем потребителям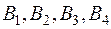 
, спрос которых равен соответственно 
, 
, 
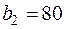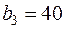и 
тонн так, чтобы затраты на транспортировку были минимальными.
Стоимость перевозки 1т (в усл. ден. ед.) указана в таблице 2.1.
Таблица 2.1.
| Хранилища | Потребители | Запас топлива, т | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потребность в топливе, т |
Решение.
Прежде, чем решать транспортную задачу необходимо проверить условие баланса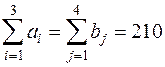 
. Поскольку запасы топлива в хранилищах равны спросу потребителей, имеем задачу закрытого типа.
Первым этапом решения является нахождение начального опорного плана методом «минимального элемента». Груз распределяется, начиная с загрузки клетки с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен.
Итак, в распределительной таблице записан исходный опорный план (таблица 2.2.):
Таблица 2.2
| Хранилища | Потребители | Запас топлива, т | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потребность в топливе, т |
или 
.
Начальный опорный план, найденный методом «минимального элемента» имеет количество занятых клеток ровно m+n-1=6, поэтому становится допустимым.
Минимальные транспортные издержки для этого плана:
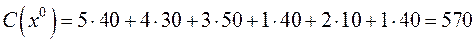(усл.ед.)
Вторым этапом решения является проверка на оптимальность допустимого плана методом потенциалов:
Каждому поставщику поставим в соответствие потенциал 
, а каждому потребителю потенциал 
.
Для каждой занятой клетки будет соответствовать уравнение:
,
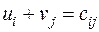где - потенциалы поставщиков; - потенциалы потребителей.
Потенциалы строк и столбцов для начального опорного плана, найденного методом «минимального элемента» получим из решения системы:
Система линейно-зависимая, для нахождения одного из решений придадим одному из потенциалов числовое значение (лучше 0), например 
, тогда
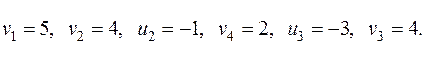
Для исследования плана на оптимальность для каждой свободной клетки считаем оценки:
;
Так как оценка 
, то найденный план не оптимален. Его можно улучшить с помощью цикла пересчета.
Составим цикл пересчета относительно клетки (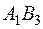
) (таблица 2.3).
Таблица 2.3.
| Хранилища | Потребители | Запас топлива, т | ||||
| В1 | В2 | В3 | В4 | |||
| А1 | 40 - | + |
| |||
| А2 | 
| |||||
| А3 | 10 + | 40 – | 
| |||
| Потребность в топливе, т | ||||||
| 
| 
| 
|
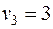
Из клеток, помеченных «– » выбираем наименьшее количество груза (40) и будем его прибавлять к клеткам, помеченным «+» и вычитать из клеток, помеченных «– », получим следующий план перевозок (таблица 2.4).
Таблица 2.4.
| Хранилища | Потребители | Запас топлива, т | ||||
| В1 | В2 | В3 | В4 | |||
| А1 |
| |||||
| А2 |
| |||||
| А3 |
| |||||
| Потребность в топливе, т | ||||||
|
|
|
|
|
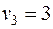
Полученный опорный план является вырожденным, т.к. число заполненных клеток равно 5<m+n-1=6. Для преодоления вырожденности плана, поставим ноль в любую пустую клетку, например в клетку (
). Проверим его на оптимальность, для этого найдем потенциалы строк и столбцов из решения системы:
Пусть , тогда
Определим оценки свободных клеток:
Так как все оценки неотрицательны, то найденный опорный план является оптимальным.
Минимальные транспортные издержки для этого плана:
(усл. ед.).
Итак, по оптимальному плану, необходимо:
- из хранилища А1 потребителю В2 доставить 20т, потребителю B3 – 40 т топлива;
- из хранилища А2 потребителю В2 доставить 50 т топлива, а потребителю В4 - 40 т топлива;
- из хранилища А3 доставить 50 т топлива потребителю В1.
При этом затраты на транспортировку будут минимальными и составят 490 усл. ден. ед.