Суть симплексного метода
Рассмотрим стандартную задачу ЛП:
,
, 
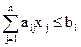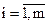, (4.1)
, 
.
В случае совместности ограничений в (4.1), можно показать, что множество допустимых решений образует выпуклую многоугольную область в n-мерном пространстве. Если эта область является ограниченной, то будем называть ее выпуклым многоугольником в n-мерном пространстве. Согласно основной теореме линейного программирования, если задача ЛП имеет решение, то целевая функция достигает оптимального значения хотя бы в одной угловой точке многоугольника решений. Если же целевая функция достигает оптимального значения более, чем в одной угловой точке, то она достигает того же самого решения в любой точке отрезка, соединяющего эти точки. Следовательно, с теоретической точки зрения задача ЛП не является сложной. Просто достаточно найти конечное число вершин многоугольника решений и вычислить в них значения целевой функции. Из всех этих значений выбрать наибольшее и наименьшее.
С практической точки зрения, дело обстоит гораздо сложнее. Во-первых, простой перебор вершин многоугольника решений может оказаться практически неосуществим из-за очень большого числа вершин многоугольника. А во-вторых, даже при небольшом количестве вершин, задача нахождения координат вершин, по трудоемкости, сопоставима с исходной задачей. Поэтому возникла необходимость применения методов целенаправленного перебора, суть которых, очевидно, заключается в том, чтобы перебирать не все вершины, а переходить от произвольной вершины к той, в которой значение целевой функции «не хуже», чем в предыдущей. Одним из таких методов является симплекс-метод.
Основные определения симплексного метода.
|
|
Считаем, что все неравенства в (4.1) имеют вид 
, если же имеются неравенства вида 
, то их легко привести к неравенству , умножив левую и правую часть неравенства на (-1). Приведем стандартную задачу ЛП (4.1) к каноническому виду. Для этого вводим дополнительные неотрицательные переменные 
, и получаем соответствующую каноническую задачу ЛП:
,
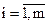, , (4.2)
, 
.
Система ограничений в (4.2) представляет собой систему m линейных уравнений, при этом ранг этой системы предполагаем равным m. Эта система имеет бесконечное число решений. В таком случае n-m переменных могут принимать произвольные значения (такие переменные будем называть свободными переменными), а остальные m переменных выражаются через свободные переменные (их будем называть базисными переменными).
Определение 4.1. Решение системы линейных уравнений, в котором все свободные переменные равны нулю, называются базисным решением.
Определение 4.2. Базисное решение, в котором все компоненты неотрицательны, называется допустимым базисным решением.
Определение 4.3. Допустимое базисное решение называется невырожденным, если в нем имеется ровно m положительных компонент, в противном случае, оно называется вырожденным.
Построение первой симплексной таблицы.
Предполагаем, что задача ЛП записана в виде (4.2). При решении задачи симплекс-методом удобно пользоваться так называемыми симплекс-таблицами. Преобразуем (4.2) следующим образом, выбрав, в качестве базисных переменных, дополнительные переменные :
,
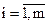, , (4.3)
, 
,
, ,
.
Следует обратить внимание, что в (4.3) перед знаками «суммы» в первой и второй строчках должен стоять знак «минус».
|
|
На основе (4.3) составляем первую симплексную таблицу.
Таб.1. Первая симплекс-таблица
| Базисные переменные | Свободные элементы | Свободные переменные | ||||
| … | 
| … | 
| ||
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
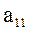
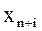
| Целевая функция F | 
| 
| … | 
| … | 
|
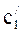
Алгоритм симплекс-метода.
1итерация.
1 шаг.
Нахождение базисного решения.
В базисном решении все свободные переменные равны нулю, а базисные переменные равны свободным элементам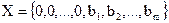 
.
2 шаг.
Проверка допустимости базисного решения.
Критерий 1. Базисное решение будет допустимым, если в симплекс-таблице все свободные элементы, кроме быть может последнего, неотрицательные.
Если базисное решение допустимо, то переходим к шагу 3, в противном случае проверяем совместность исходных ограничений.
Критерий 2. Проверка совместности ограничений. Ограничения несовместны, если хотя бы в одной строке, кроме последней, с отрицательным свободным элементом, все значения положительные.
Если выявлена несовместность, то решения у задачи нет.
Если несовместность не выявлена и базисное решение недопустимо, то переходим к шагу 4.
3 шаг.
Проверка оптимальности решения.
Если базисное решение допустимое, то решение проверяется на оптимальность с помощью критерия 3.
Критерий 3. Целевая функция будет иметь максимальное (минимальное) значение, если последние элементы столбцов «свободные переменные» будут неотрицательными (неположительными). При этом, максимальное (минимальное) значение целевой функции равно последнему элементу в столбце «свободные элементы».
|
|
Если допустимое базисное решение неоптимальное, то необходимо проверить ограниченность целевой функции согласно критерию 4.
Критерий 4. Целевая функция ограничена сверху (снизу), т.е. существует максимальное (минимальное) значение целевой функции, если на каждой итерации в каждом столбце, не удовлетворяющем признаку оптимальности, есть хотя бы один положительный, не последний в столбце, элемент.
Если выявлена неограниченность целевой функции сверху (снизу), то точки максимума (минимума) не существует.
Если не выявлено неограниченность целевой функции сверху (снизу), то переходим к шагу 4.
4 шаг.
Нахождение разрешающего элемента.
1. Нахождение разрешающего столбца.
а) базисное решение недопустимое.
В строке, содержащей отрицательный свободный элемент (кроме последней строки), выбирается отрицательный элемент. Столбец j, в котором находится выбранный элемент, принимается в качестве разрешающего;
б) базисное решение допустимое, неоптимальное.
В качестве разрешающего столбца принимается любой столбец «свободные переменные», последний элемент которого не удовлетворяет критерию оптимальности 3.
2. Нахождение разрешающей строки.
Составляются дроби вида 
, где 
есть элементы разрешающего столбца j, а 
есть свободные элементы, при этом 
имеют одинаковый знак. В качестве разрешающей строки, выбирается та, для которой найденное значение дроби минимальное.
Замечание. Если выбор разрешающего элемента неоднозначный, то можно выбрать любой из них. Это может несущественно повлиять лишь на количество итераций, но не влияет на оптимальное решение. На практике рекомендуется выбрать наименьший из отрицательных элементов и наибольший из положительных.
После нахождения разрешающего элемента переходим к шагу 5.
5 шаг.
Преобразование симплекс-таблицы.
Предположим, что разрешающий элемент является 
, который выделен рамкой в таб.1. В этом случае базисную переменную 
необходимо перевести в свободные, а свободную переменную 
- в базисные. При этом составляется новая симплекс-таблица, которая заполняется по следующим правилам.
1. На месте разрешающего элемента записывается значение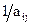 
.
2. Элементы разрешающей строки делятся на разрешающий элемент, т.е.
, 
, 
, 
.
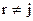3. Элементы разрешающего столбца делятся на разрешающий элемент и берутся с обратным знаком, т.е.
, 
, 
, 
.
4. Остальные элементы 
, 
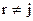, заполняются по правилу прямоугольника. Вначале строится прямоугольник, одной из вершин которого является элемент, требующий изменения, а противоположной вершиной всегда является разрешающий элемент. Затем из элемента, требующего изменения, вычитается дробь, знаменатель в которой равен разрешающему элементу, а числитель есть произведение двух других вершин прямоугольника, т.е.:
,
,
, 
,
, , , .
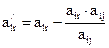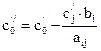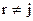В результате преобразования получим новую симплекс-таблицу (таб.2).
Таб.2. Преобразованная симплекс-таблица
| Базисные перем. | Свобод. Элементы | Свободные переменные | ||||
| … | 
| … |
| ||
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
| … | … | … | … | … | … | … |
| 
| 
| … | 
| … | 
|
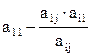
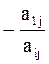
| Целевая функция F | 
| 
| … | 
| … | 
|
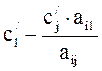
После выполнения шага 5, необходимо перейти ко второй итерации, начиная с шага 1, но использую уже преобразованную таблицу.
Пример. Найти наибольшее значение целевой функции F при заданных ограничениях:
Подготовим условия задачи к симплекс-методу. Для этого, вначале приведем все неравенства к виду . Для этого умножим левую и правую часть третьего неравенства на (-1) и получим:
Теперь введем в каждом неравенстве дополнительные переменные, чтобы перейти к канонической задаче ЛП:
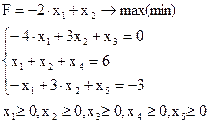
В качестве базисных переменных удобно выбрать дополнительные переменные 
и запишем систему в виде (4.3):
Составим первую симплекс-таблицу.
| Базисные переменные | Свободные элементы | Свободные переменные | |
| X1 | X2 | ||
| X3 | –4 | ||
| X4 | |||
| X5 | –3 | –1 | |
| F | –1 |
1 итерация.
1 шаг. Находим базисное решение. В базисном решении все свободные переменные равны 0, а базисные переменные равны соответствующим свободным элементам:
2 шаг. Проверяем допустимость полученного базисного решения. Оно является недопустимым, т.к. имеется отрицательный элемент (-3).
3 шаг. Проверяем совместность ограничений. Ограничения совместны, т.к. в строке с отрицательным свободным элементом (-3) имеются ещё отрицательный элемент (-1).
Так как несовместность не выявлена, мы переходим к шагу 4.
4 шаг. Необходимо найти разрешающий элемент.
Найдем разрешающий столбец. Мы имеем пункт а). Выберем наименьший отрицательный элемент в строке с отрицательным свободным элементом (-3). Такой элемент единственный, это (-1). Столбец, в котором находится этот элемент (это столбец 
), принимаем в качестве разрешающего столбца.
Для нахождения разрешающей строки определяем минимальное положительное отношение свободных элементов к элементам разрешающего столбца. Так как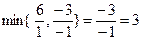 
, то в качестве разрешающей строки получаем 
.
Элемент, находящийся на пересечении разрешающих столбца и строки, является разрешающим элементом (выделен рамкой). Он указывает, что базисную переменную переводим в свободные, а свободную переменную – в базисные.
5 шаг.
Преобразуем симплекс-таблицу, используя правила преобразования:
1. На месте разрешающего элемента записывается значение 
.
2. Элементы разрешающей строки делятся на разрешающий элемент (–1).
3. Элементы разрешающего столбца делятся на разрешающий элемент (–1) и берутся с обратным знаком.
4. Остальные элементы заполняются по правилу прямоугольника. Например, элемент, находящийся на пересечении столбца 
и строки 
, будет равен 
.
В результате преобразования симплекс-таблицы получим:
| Базисные переменные | Свободные элементы | Свободные переменные | |
| X5 | X2 | ||
| X3 | -4 | -9 | |
| X4 | 
| ||
| X1 | -1 | -3 | |
| F | -6 |
2 итерация.
1 шаг. Находим базисное решение.
2 шаг. Проверяем допустимость полученного базисного решения. Оно является допустимым, т. к. все его компоненты не отрицательны.
Так как базисное решение является допустимым, то мы переходим к шагу 3.
3 шаг. Все последние элементы столбцов «свободные переменные» являются положительными (2 и 5), следовательно, найденное допустимое базисное решение доставляет максимум целевой функции и максимальное значение целевой функции равно последнему элементу в столбце «свободные элементы»:
.
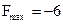Найдем теперь минимум целевой функции. Так как у нас имеется допустимое базисное решение, но оно не доставляет минимум целевой функции, то нам необходимо проверить ограниченность функции снизу согласно критерию 4, по которому целевая функция ограничена снизу, если в каждом столбце, не удовлетворяющем признаку оптимальности, есть хотя бы один положительный элемент. У нас оба столбца «свободные переменные» не удовлетворяют критерию оптимальности на минимум, т. к. оба последних элемента (2 и 5) являются положительными. В этих столбцах есть положительные элементы (1 и 4), следовательно, неограниченность снизу не выявлена и мы переходим к шагу 4.
4 шаг. Необходимо найти разрешающий элемент.
Найдем разрешающий столбец. Мы имеем пункт б). Выберем любой столбец «свободных переменных», последний элемент которого не удовлетворяет критерию оптимальности на минимум. Так как у нас оба столбца не удовлетворяют критерию оптимальности, то из положительных элементов выбираем наибольший, а среди 2 и 5 наибольший есть 5 и, следовательно, столбец будет разрешающим.
Для нахождения разрешающей строки определяем минимальное положительное отношение свободных элементов к элементам разрешающего столбца. Находим:
, то в качестве разрешающей строки получаем 
.
Элемент, находящийся на пересечении разрешающих столбца и строки, является разрешающим элементом (выделен рамкой). Он указывает, что базисную переменную переводим в свободные, а свободную переменную - в базисные.
5 шаг. Преобразуем симплекс-таблицу и получаем:
| Базисные переменные | Свободные элементы | Свободные переменные | |
| X5 | X4 | ||
| X3 |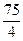 
| 
| 
|
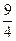
| X2 | 
| 
| 
|
| X1 | 
| 
|
|
| F | 
|
| 
|
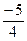
3 итерация.
1 шаг. Находим базисное решение.
2 шаг. Проверяем допустимость полученного базисного решения. Оно является допустимым, т. к. все его компоненты не отрицательны.
Так как базисное решение является допустимым, то мы переходим к шагу 3.
3 шаг. Допустимое базисное решение не доставляет минимум целевой функции, т. к. один из последних элементов столбцов «свободная переменная» является положительным, это .
Так как у нас имеется допустимое базисное решение, но оно не доставляет минимум целевой функции, то нам необходимо проверить ограниченность функции снизу согласно критерию 4, по которому целевая функция ограничена снизу, если в каждом столбце, не удовлетворяющем признаку оптимальности, есть хотя бы один положительный элемент. В столбце есть положительный элемент (), следовательно неограниченность снизу не выявлена и мы переходим к шагу 4.
Выполняя действия, аналогичные действиям на итерации 2, получаем симплекс-таблицу:
| Базисные переменные | Свободные элементы | Свободные переменные | |
| X2 | X4 | ||
| X3 | |||
| X5 | |||
| X1 | |||
| F | –12 | –3 | –2 |
4 итерация.
1 шаг. Находим базисное решение.
2 шаг. Проверяем допустимость полученного базисного решения. Оно является допустимым, т. к. все его компоненты не отрицательны.
Так как базисное решение является допустимым, то мы переходим к шагу 3.
3 шаг. Допустимое базисное решение доставляет минимум целевой функции, т. к. все последние элементы столбцов «свободная переменная» являются отрицательными и, при этом, 
Таким образом, наибольшее значение 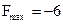целевая функция имеет при 
, а наименьшее значение при 
. Видим, что оптимальные решения, найденные симплекс-методом, полностью совпадают с решениями, найденными геометрическим методом.