Имеется три поставщика некоторого товара А1, А2, А3, у которых соответственно имеются 160, 310 и 250 условных единиц (у. е.) товара. В данном товаре нуждаются города B1, B2, B3, B4 в количествах, равных, соответственно, 100, 170, 200 и 250 у. е. Стоимость перевозки единицы продукции от поставщиков к потребителям задается следующей таблицей:
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
Составим экономико-математическую модель данной задачи.
Обозначим через 
- объём перевозки от поставщика Аi к потребителю Bj.
Тогда суммарные затраты на перевозку F составят:
Заданные мощности поставщиков и спрос потребителей накладывают ограничения на значения объемов перевозок 
:
мощности всех поставщиков должны быть реализованы:
Спросы потребителей должны быть удовлетворены:
Объемы перевозимых грузов не могут быть отрицательными:
Выясним характер транспортной задачи, т. е. является ли она открытой или закрытой.
В силу того, что
т. е. суммарная мощность равна суммарному спросу, то данная задача является закрытой.
Находим первоначальное базисное распределение поставок методом наименьших затрат.
Находим в таблице клетку с наименьшим коэффициентом затрат. Таких клеток у нас две, а именно: (1,1) и (2,4). В этих клетках коэффициент затрат равен 5. Находим максимально возможные поставки в эти клетки:
Здесь мы учитываем, что первый поставщик имеет груз в количестве 160, но первому потребителю надо только 100.
.
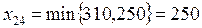Наибольшая максимально возможная поставка будет в клетку (2,4). Поэтому реализуем эту поставку в клетку (2,4), т. е. даем этой клетке груз в количестве 250 у.е. Тогда, спрос четвертого потребителя полностью будет удовлетворен. Клетку (2,4) считаем заполненной, и перечеркиваем ее жирной сплошной линией. При этом выпадают из дальнейшего рассмотрения остальные клетки четвертого столбца (спрос четвертого потребителя полностью удовлетворен), их перечеркиваем тонкими линиями.
|
|
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
В оставшихся не перечеркнутых никакой линией клетках находим клетку с наименьшим коэффициентом затрат. Это клетка (1,1). Максимально возможную поставку в эту клетку мы уже нашли: 
. Реализуем эту поставку, при этом спрос первого потребителя будет полностью удовлетворен и, следовательно, из дальнейшего рассмотрения выпадет первый столбец и таблица будет иметь вид:
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
В оставшихся не перечеркнутых никакой линией клетках находим клетку с наименьшим коэффициентом затрат. Это клетка (1,2), коэффициент затрат в которой равен 8. Максимально возможная поставка в эту клетку будет:
.
Здесь мы учли, что от первого поставщика мы взяли 100 у. е. груза для первого потребителя. Реализуем поставку, при этом мощность первого поставщика будет полностью реализована, и, следовательно, из дальнейшего рассмотрения выпадет первая строка и таблица будет иметь вид:
|
|
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
В оставшихся не перечеркнутых никакой линией клетках находим клетку с наименьшим коэффициентом затрат. Это клетка (2,3), коэффициент затрат в которой равен 9. Максимально возможная поставка в эту клетку будет:
.
Реализуем эту поставку, при этом мощность второго поставщика будет полностью реализована, и, следовательно, из дальнейшего рассмотрения выпадет вторая строка, и таблица будет иметь вид:
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
В оставшихся не перечеркнутых никакой линией клетках находим клетку с наименьшим коэффициентом затрат. Это клетка (3,3), коэффициент затрат в которой равен 10. Максимально возможная поставка в эту клетку будет:
.
Реализуем эту поставку, при этом спрос третьего потребителя полностью будет удовлетворен, и таблица будет иметь вид:
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
Из не перечеркнутых никакой линией клетках осталась одна клетка. Это клетка (3,2), коэффициент затрат в которой равен 17. Максимально возможная поставка в эту клетку будет:
|
|
.
Реализуем эту поставку, при этом получим первоначальное базисное распределение поставок:
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
Проверка (обязательна!).
После нахождения первоначального распределения поставок необходимо выполнить две проверки.
1 проверка. Необходимо проверить суммы по строкам, которые должны совпадать с мощностями поставщиков и суммы по столбцам, которые должны совпадать со спросами потребителей. Для нашего примера:
суммы по строкам:
100+60=160
60+250=310
110+140=250
суммы по столбцам:
100=100
60+110=170
60+140=200
250=250.
Видим, что совпадают.
2 проверка. Количество заполненных клеток должно быть равно m+n-1.
Как было замечено выше, в методе наименьших затрат, в процессе заполнения таблицы, могут одновременно выпасть строка и столбец, т.е. количество клеток будет меньше (m+n-1). В таком случае в некоторую свободную клетку поставляют фиктивную нулевую поставку, с которой в дальнейшем работают также как и с другими.
Проверяем количество заполненных клеток (перечеркнутых жирной линией). Их 6, а m+n-1=4+3-1=6. В нашем примере не нужно вводить фиктивные нулевые поставки.
Найдем суммарные затраты на перевозку груза при первоначальном распределении поставок:
Метод потенциалов
После того, как было найдено первоначальное распределение поставок, необходимо, для нахождения оптимального распределения поставок, применить метод потенциалов.
1 шаг. Нахождение потенциалов строк и столбцов.
Вычисляются потенциалы поставщиков 
и потребителей 
. Полагают, что потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию:
Число занятых клеток равно (m+n-1) и, следовательно, для определения потенциалов, надо решать систему из (m+n-1) уравнений с (m+n) неизвестными. Система является неопределенной, т. е. имеет бесконечное множество решений, поэтому для облегчения нахождения частного решения полагают 
. Далее двигаются по заполненным клеткам и находят остальные потенциалы.
2 шаг. Нахождение матрицы оценок.
Вычисляются матрица оценок с элементами, определяемыми следующим образом:
Если все элементы матрицы оценок неотрицательны, т. е.
то найденное распределение поставок будет оптимальным. Если для всех ячеек 
, то оптимальный распределение поставок является единственным. Если какая-либо оценка 
, то существует бесчисленное множество решений с одинаковым значением целевой функции.
Если какое-либо значение 
, то найденное распределение поставок не является оптимальным и необходимо строить так называемый цикл пересчета, в котором перераспределяются поставки.
3 шаг. Построение цикла пересчета.
Среди отрицательных элементов матрицы оценок выбираем наименьшее. Клетка (она, кстати, всегда будет свободной) с таким значением будет вершиной цикла пересчета.
Цикл пересчета представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся только под прямым углом. В одной строке (столбце) может быть только одно звено, соединяющее только две клетки.
В цикле всего одна свободная клетка, остальные заполненные. В цикле всегда четное число клеток. В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.
В клетках со знаком «–» находим наименьшую поставку, которую передаем по циклу. В клетки с «+» эту поставку прибавляем, с «–», соответственно, вычитаем. Если при этом сразу в нескольких клетках получается 0, то только в одной клетке ничего не пишем, т.е. считаем ее свободной, а в остальные обнулившиеся клетки записываем формально нулевую поставку.
Измененные значения клеток цикла пересчета ставим в распределительную таблицу и возвращаемся к шагу 1.
Пример. Найдем оптимальное распределение поставок для нашего примера. Вначале перепишем таблицу с первоначальным распределением поставок в виде:
| |||||
| |||||
1 итерация.
1 шаг. Нахождение потенциалов строк и столбцов.
Определим потенциалы поставщиков 
и потребителей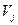 
. Полагают, что потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию:
При этом полагают 
. Далее двигаются по заполненным клеткам и находят остальные потенциалы.
Двигаемся по первой строке распределительной таблицы. Заполненных клеток здесь две: (1,1) и (1,2). Вначале идем до клетки (1,1). Этой клетке соответствует потенциал первой строки 
(т. к. клетка находится в первой строке) и потенциал первого столбца 
(клетка находится в первом столбце). Должно выполняться равенство:
Мы потребовали, чтобы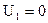 
. Значение 
. Следовательно, значение 
. Записываем его в последней сроке распределительной таблицы.
В первой строке распределительной таблицы есть, как было указано выше, еще одна заполненная клетка. Это клетка (1,2). Этой клетке соответствует потенциал первой строки (т. к. клетка находится в первой строке) и потенциал второго столбца 
(клетка находится во втором столбце). Должно выполняться равенство:
Мы потребовали, чтобы 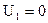. Значение 
. Следовательно, значение 
. Записываем его в последней сроке распределительной таблицы.
Больше никакой информации из первой строки мы не можем почерпнуть, т. к. в ней нет больше заполненных клеток. Поэтому рассматриваем столбцы, для которых мы нашли потенциалы. Это первый и второй столбцы.
Смотрим на первый столбец. В нем только одна заполненная клетка, и мы ее уже использовали для нахождения потенциала первого столбца.
Смотрим на второй столбец. В нем, кроме уже использованной заполненной клетки в первой строке, есть еще одна заполненная клетка в третьей строке, а именно клетка (3,2). Этой клетке соответствует потенциал третьей строки 
(т. к. клетка находится в третьей строке) и потенциал второго столбца (клетка находится во втором столбце). Должно выполняться равенство:
Мы нашли, что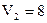 
. Значение 
. Следовательно, значение 
. Записываем его в последнем столбце распределительной таблицы.
Больше заполненных клеток в столбце 2 нет, и мы не можем больше почерпнуть информацию из него.
Но мы теперь знаем потенциал еще одной строки. Это строка 3. В этой строке есть две заполненные клетки. Одну мы уже использовали для нахождения потенциала третьей строки. Рассмотрим другую заполненную клетку в третьей строке, а именно клетку (3,3). Этой клетке соответствует потенциал третьей строки и потенциал третьего столбца 
. Должно выполняться равенство:
Мы нашли, что 
. Значение 
. Следовательно, значение 
. Записываем его в последней строке распределительной таблицы.
Далее смотрим на третий столбец. В нем есть заполненная клетка (2,3). Совершая действия, аналогичные выше рассмотренным, находим, что потенциал второй строки равен 8, а потенциал четвертого столбца равен –3. В результате получили следующую таблицу:
|
| |||||
|
| |||||
| |||||
|
| |||||
|
| 
|
| 
| 
| |
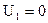
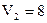
2 шаг. Нахождение матрицы оценок.
Вычисляются матрица оценок с элементами, определяемыми следующим образом:
Получаем матрицу оценок:
3 шаг. Построение цикла пересчета.
Среди отрицательных элементов матрицы оценок выбираем наименьшее. В нашем случае это –6, которое находится в клетке (2,1). Эта свободная клетка будет вершиной цикла пересчета. Цикл пересчета, как было указано выше, представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся только под прямым углом. В одной строке (столбце) может быть только одно звено, соединяющее только две клетки.
В цикле всего одна свободная клетка, остальные заполненные.
Мы двигаемся из клетки (2,1). Далее идем только по заполненным клеткам так, чтобы вернуться назад, и при этом учитываем все вышеперечисленные правила. Поэтому получаем следующий путь:
В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.
Из клеток со знаком «–» находим наименьшую поставку. У нас три клетки со знаком «–». Это клетки (1,1), (2,3) и (3,2). Наименьшая поставка находится в клетке (2,3) и она равна 60. Эту поставку передаем по циклу. В клетки с «+» ее прибавляем, с «–», соответственно, вычитаем. Например, клетка (3,3) со знаком «+», старая поставка в ней равнялась 140, прибавляем к ней 60, получаем 200. Клетка (3,2) была со знаком «–» и старая поставка в ней равнялась 110. Отнимаем 60 и получаем, что новая поставка в этой клетке равна 50. Свободная клетка (2,1) становится заполненной клеткой с поставкой 60, а ранее заполненная клетка (2,3) становится заполненной. Окончательно получаем новую распределительную таблицу:
|
| |||||
|
| |||||
| |||||
| |||||
|
| 
|
|
| 
| |
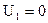
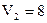
2 итерация.
1 шаг. Нахождение потенциалов строк и столбцов.
Находим потенциалы строк и столбцов.
2 шаг. Нахождение матрицы оценок.
Получаем матрицу оценок:
3 шаг. Построение цикла пересчета.
Среди отрицательных элементов матрицы оценок выбираем наименьшее. В нашем случае это –5, которое находится в клетке (3,4). Эта свободная клетка будет вершиной цикла пересчета. Строим цикл пересчета.
При построении цикла мы учли правило о том, что в одной строке (столбце) может быть только одно звено, соединяющее только две клетки. В третьей строке две заполненные клетки. Клетку (3,3) мы из цикла исключаем.
В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.
Из клеток со знаком «–» находим наименьшую поставку. У нас три клетки со знаком «–». Это клетки (1,1), (2,4) и (3,2). Наименьшая поставка находится в клетке (1,1) и она равна 40. Эту поставку передаем по циклу. В клетки с «+» ее прибавляем, с «–», соответственно, вычитаем.
Окончательно получаем новую распределительную таблицу:
|
| |||||
|
| |||||
| |||||
|
| |||||
|
| 
|
|
| 
| |
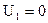
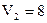
3 итерация.
1 шаг. Нахождение потенциалов строк и столбцов.
Находим потенциалы строк и столбцов.
2 шаг. Нахождение матрицы оценок.
Получаем матрицу оценок:
3 шаг. Построение цикла пересчета.
Среди отрицательных элементов матрицы оценок выбираем наименьшее. В нашем случае это –3, которое находится в клетке (2,2). Эта свободная клетка будет вершиной цикла пересчета. Строим цикл пересчета.
В вершинах цикла условно ставим знаки: в свободную клетку цикла ставим «+». Затем знаки чередуются.
Из клеток со знаком «–» находим наименьшую поставку. У нас две клетки со знаком «–». Это клетки (2,4) и (3,2). Наименьшая поставка находится в клетке (3,2) и она равна 10. Эту поставку передаем по циклу. В клетки с «+» ее прибавляем, с «–», соответственно, вычитаем.
Окончательно получаем новую распределительную таблицу:
|
| |||||
|
| |||||
| |||||
| |||||
|
| 
|
| 
| 
| |
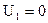
4 итерация.
1 шаг. Нахождение потенциалов строк и столбцов.
Находим потенциалы строк и столбцов.
2 шаг. Нахождение матрицы оценок.
Получаем матрицу оценок:
Получили, что все элементы матрицы оценок неотрицательные, следовательно получили оптимальное распределение поставок. Найдем наименьшие затраты на перевозку груза:
Напомним, что при первоначальном распределении поставок, найденном методом наименьших затрат, суммарные затраты составили 6040 у. е.
Ответ. Оптимальный план распределения:
Минимальные суммарные затраты составляют 5450 у.е.