Методы оптимальных решений
Вопросы к зачету:
1. Общая, стандартная и каноническая задачи ЛП.
2. Графическая интерпретация и графический метод решения задач ЛП.
3. Алгоритм симплекс-метода.
4. Получение первого базисного решения.
5. Признаки совместности ограничений, допустимости, оптимальности и альтернативности базисного решения, ограниченности целевой функции.
6. Определение разрешающего элемента.
7. Правила преобразования симплекс-таблицы.
8. Двойственная задача ЛП.
9. Экономическая интерпретация двойственной задачи ЛП.
10. Первая теорема двойственности.
11. Вторая теорема двойственности.
12. Двойственные оценки и их экономический смысл. Интервалы устойчивости двойственных оценок.
13. Задача использования ресурсов с ограничениями на технико-экономические показатели.
14. Задача использования взаимозаменяемых ресурсов.
15. Метод потенциалов.
16. Метод наименьших затрат для решения транспортных задач.
17. Динамическое программирование. Признак оптимальности. Уравнения Белмана.
18. Задача распределения ресурсов между отраслями (предприятиями).
19. Задача нахождения оптимального маршрута.
20. Задача замены оборудования.
21. Задача распределения ресурсов между двумя предприятиями на n лет.
22. Упорядочение сетевого графика.
23. Нахождение параметров событий: раннего срока,
24. позднего срока свершения события.
25. Определение критического пути с помощью параметров событий.
26. Нахождение параметров работ. Нахождение резерва времени пути, полного резерва времени работы, частного резерва первого вида, свободного резерва.
27. Определение критического пути с помощью параметров работ.
28. Сетевое планирование в условиях неопределенности.
|
|
29. Оптимизация сетевого графика методом «время-стоимость».
Введение
При решении практических задач в экономике, производственном менеджменте часто возникает необходимость нахождения максимальной прибыли, минимальных затрат при выполнении некоторых экономических, природных и т. п. ограничений. С математической точки зрения, вышесказанное может означать необходимость нахождения максимума или минимума некоторой функции многих переменных:
, (1)
когда на эти переменные накладываются некоторые ограничения вида:
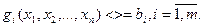(2)
Задачи подобного рода называются задачами математического программирования. Функция (1) называется целевой функцией. Функции f и 
– есть некоторые заданные функции. В формуле (2) 
есть заданные константы.
Существует множество разделов математического программирования, которые решают свой класс задач, зависящий от типа функций (1) и (2).
Если целевая функция (1) и все функции в (2) являются линейными, то задача (1), (2) решается методами линейного программирования.
Если целевая функция (1) и (или) хотя бы одна из функций в (2) являются нелинейными, то задача (1), (2) решается методами нелинейного программирования.
Если требуется, чтобы решение задачи (1), (2) выражалось целыми числами, то применяют методы целочисленного программирования.
Если в (1) или в (2) содержатся случайные величины, то задача решается методами стохастического программирования.
Также еще существует выпуклое, параметрическое и динамическое программирование.
В данной работе «Методы и модели в экономике» мы рассмотрим некоторые разделы линейного программирования.
Часть I. Геометрический метод. Симплекс-метод