Постановка транспортной задачи

Имеется m поставщиков , у которых сосредоточен однородный груз в количествах соответственно . Значения называются мощностями поставщиков. Этот груз необходимо распределить между n потребителями , спрос которых равен соответственно . Известна стоимость перевозки единицы груза от i – го поставщика к j - му потребителю, которую обозначим через .

Необходимо найти оптимальный план перевозок, который:

1) реализует мощности всех поставщиков;

2) удовлетворяет спрос всех потребителей;

3) минимизирует суммарные затраты на перевозку.

Составим экономико-математическую модель транспортной задачи. Для этого составим распределительную таблицу вида:

	Спрос потребителей
			……		……
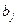
Мощности Поставщиков			……		……
……	……	……	…….	……	……
		……		……
……	……	……	………	……	……
		……		……

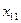
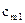
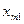
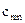
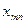
В этой таблице - количество единиц груза, которое необходимо доставить от i – го поставщика к j - му потребителю. Матрица, составленная из элементов называется матрицей перевозок. Матрица, составленная из значений , называется матрицей тарифов.

Используя введенные обозначения, можно записать, что транспортная задача заключается в нахождении такого плана перевозок , чтобы:

1) мощности всех поставщиков были реализованы, т.е. чтобы все поставщики полностью избавились от своего груза:

(1.1)

2) спрос всех потребителей был удовлетворен:

(1.2)

3) по смыслу задачи, каждая перевозка должна быть неотрицательной, т. е. должно выполняться:

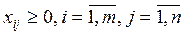(1.3)

4) суммарная стоимость перевозок была минимальной:

(1.4)

Таким образом, с математической точки зрения транспортная задача заключается в нахождении значений , удовлетворяющих (1.1)-(1.3), и таких, что функция (1.4) принимает минимальное значение. Несложно заметить, что транспортная задача есть каноническая задача ЛП.

Определение 1.1. Решение , удовлетворяющее (1.1)-(1.3), называется базисным распределением поставок.

Определение 1.2. Базисное распределение поставок, доставляющее минимум функции (1.4), называется оптимальным распределением поставок.

Определение 1.3. Транспортная задача называется закрытой, если суммарный объём груза, имеющийся у поставщиков, равен суммарному спросу потребителей, т.е. выполняется условие:

.

Если это условие не выполняется, т. е.:

,

то транспортная задача называется открытой.

Открытую транспортную задачу можно свести к закрытой следующим образом.

Если , то открытая транспортная задача сводится к закрытой путем введения фиктивного потребителя со спросом . С экономической точки зрения, нового фиктивного потребителя можно рассматривать в качестве склада. Коэффициенты в новом столбце, полагают равными 0.

Если , то вводится фиктивный поставщик с объемом груза и стоимостями перевозок, равными нулю.

Открытую транспортную задачу необходимо сводить к закрытой в силу следующей теоремы.

Теорема о существовании допустимого плана. Транспортная задача имеет допустимое распределение поставок тогда, когда выполняется следующее равенство:

Число переменных в транспортной задаче с m поставщиками и n потребителями равно nm, а число уравнений в системах (1.1) и (1.2) равно n+m. Так как предполагается, что выполняется условие , то число линейных независимых уравнений равно n+m-1. Следовательно, допустимое решение транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.

Если в допустимом решении транспортной задачи число ненулевых компонент равно n+m-1, то решение называется невырожденным, а если меньше – то вырожденным.

Как было указано выше, транспортная задача является канонической задачей линейного программирования, и для ее решения в принципе можно использовать симплекс-метод. Однако, в силу специфичности транспортной задачи, используются более эффективные методы.