Пример. Имеются три поставщика некоторого товара А1, А2, А3, на которых соответственно имеются 160, 310 и 250 условных единиц (у. е.) товара. В данном товаре нуждаются города B1, B2, B3, B4 в количествах у. е. товара, равных соответственно 100, 170, 200 и 200 у. е. Стоимость перевозки единицы продукции от поставщиков к потребителям задается следующей таблицей:
| Поставщики | Мощность Поставщиков | Потребители и их спрос | |||
| B1 | B2 | B3 | B4 | ||
| А1 | |||||
| А2 | |||||
| А3 |
Выясним характер транспортной задачи.
В силу того, что 
, т.е. суммарная мощность не равна суммарному спросу, то данная задача является открытой. Суммарный спрос потребителей меньше суммарной мощности поставщиков на 50 у. е. Поэтому нам необходимо ввести фиктивного потребителя со спросом 50 у. е. и добавить в таблицу еще один столбец. Коэффициенты затрат в этом столбце поставим нулевые.
| Поставщики | Мощность поставщиков | Потребители и их спрос | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 |
Далее задачу решаем аналогично закрытой транспортной задаче. Выбираем наименьший коэффициент затрат. Это, например, 0 в первой строке. Даем в клетку (1,5) поставку 50, выпадает первый столбец и т. д.
Решение транспортной задачи в Mathcad
После открытия пакета Mathcad набрать текст, аналогичный следующему.
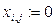
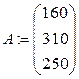
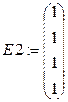
Given
Задания для самостоятельной работы
Номер варианта равен порядковому номеру в списке группы.
Задача 1.
Найти максимальное и минимальное значения целевой функции в задаче своего варианта геометрическим методом, симплекс-методом и в Mathcad. Варианты задач для самостоятельной работы
|
|
1 
| 2 
| 3 
|
4 
| 5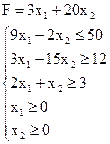 
| 6 
|
7 
| 8 
| 9 
|
10 
| 11 
| 12 
|
13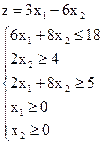 
| 14 
| 15 
|
16 
| 17 
| 18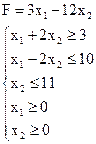 
|
19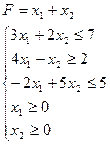 
| 20 
| 21 
|
22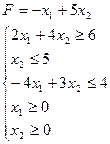 
| 23 
| 24 
|
25 
| 26 
| 27 
|
28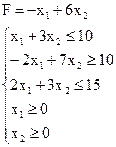 
| 29 
| 30 
|
Задача 2.
Из районов 
, в которых запасы зерна составляют соответственно 180, 70 и 50 тысяч тонн, зерно перевозится на четыре элеватора 
мощностью 50, 50, 110 и 90 тысяч тонн. Затраты на перевозку одной тонны зерна (в тыс. руб.) из районов на элеваторы задается следующей матрицей тарифов:
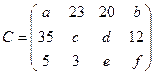
Требуется составить план перевозок, имеющий минимальные суммарные транспортные издержки. Значения параметров a, b, c, d, e, f для различных вариантов заданий приведены в таблице:
| Вариант | a | b | c | d | e | f | Вариант | a | b | c | d | e | f |
Задача 3.
|
|
На четырех шахтах 
добывают уголь для производства электроэнергии. Известно, что за некоторый период на шахтах добывается, соответственно 180, 70, 30 и 150 тысяч тонн. Для обеспечения четырех ТЭЦ 
топливом необходимо 50, 50, 110 и 90 тысяч тонн угля. Затраты на перевозку одной тонны угля (в тыс. руб.) из шахт на ТЭЦ задается следующей матрицей тарифов:
Требуется составить план перевозок, имеющий минимальные суммарные транспортные издержки. Значения параметров a, b, c, d, e, f для различных вариантов заданий приведены в таблице:
| Вариант | a | b | c | d | e | f | Вариант | a | b | c | d | e | f |
Литература
|
|
1. Исследование операций в экономике: учебн. пособие для вузов/ Н.Ш.Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2000. – 407 с.
2. Кузнецов А.В. Высшая математика: Мат. программир.: учеб./А.В. Кузнецов, В.А. Сакович, Н.И. Холод; под общ. ред. А.В. Кузнецова. – Мн.: Высш. шк., 1994. – 286 с.: ил.
3. Плис А.И., Сливина Н.А. Mathcad 2000 Математический практикум для экономистов и инженеров: учеб. пособие. – М.: Финансы и статистика, 2000. – 656 с.
Оглавление
Введение. 3
Часть I. Геометрический метод. Симплекс-метод. 3
1. Задача использования ресурсов. 3
2. Постановка задачи линейного программирования. 3
3. Геометрический метод линейного программирования. 3
4. Симплексный метод линейного программирования. 3
5. Решение задачи линейного программирования в Mathcad. 3
Часть II. Транспортная задача. 3
1. Постановка транспортной задачи. 3
2. Методы решения транспортной задачи. 3
2.1. Нахождение первоначального базисного распределения поставок 3
2.2 Пример закрытой транспортной задачи. 3
2.3. Метод потенциалов. 3
2.4. Пример открытой транспортной задачи. 3
2.5. Решение транспортной задачи в Mathcad. 3
Задания для самостоятельной работы.. 3
Литература. 3
Оглавление. 3