Транспортная задача решается в два этапа. На первом этапе находят любое допустимое решение, удовлетворяющее системам (1.1)-(1.3). Такое решение называется первоначальным базисным распределением поставок. Затем, с помощью метода потенциалов, делают такие преобразования с первоначальным распределением поставок, чтобы получить оптимальное распределение поставок. Рассмотрим вначале нахождение первоначального базисного распределения поставок.
Нахождение первоначального базисного распределения поставок
Первоначальное базисное распределение поставок можно находить различными методами. Рассмотрим основные из них.
Метод северо-западного угла.
В этом методе груз распределяем от верхней левой клетки (1, 1), называемой северо-западной, двигаясь затем от нее по строке вправо или по столбцу вниз. Полагаем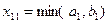 
. Если 
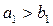, то полагают 
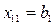и первый потребитель будет полностью удовлетворен. Тогда, в дальнейшем первый столбец выпадает и полагаем 
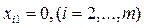. Если в клетку мы дали поставку, то считаем ее заполненной, и перечеркиваем ее, для удобства, сплошной линией. Выпавшие из дальнейшего рассмотрения клетки, считаем свободными, и перечеркиваем их пунктирной линией.
Затем двигаемся по первой строке таблицы и заносим в клетку (1,2) 
. Если 
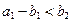, то запасы первого поставщика исчерпаны и из дальнейшего рассмотрения выпадает первая строка.
Далее переходим ко второму поставщику. Если 
, то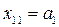 
, значит запас первого поставщика исчерпан, т.е. 
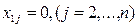и первая строка выпадает. Переходим в клетку (2, 1) при этом 
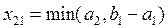. После заполнения клетки (1, 2) или (2, 1) переходим ко второй строке или ко второму столбцу и т.д., пока не исчерпаются все ресурсы.
Метод наименьших затрат
|
|
Вначале находится клетка с наименьшим коэффициентом затрат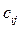 
. Затем в нее записывается максимально возможная поставка и из рассмотрения исключают или выпавшую при этом строку, или столбец.
Затем выбираем наименьший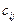 
из оставшихся клеток до тех пор, пока мощность всех поставщиков не будет реализована, а спрос всех потребителей не будет удовлетворен.
В этом методе в процессе заполнения таблицы могут одновременно выпасть строка и столбец, т.е. количество клеток будет меньше (m+n-1). В данном случае в некоторую свободную клетку поставляют фиктивную нулевую поставку. Эта клетка будет считаться заполненной, и в дальнейшем с ней работают так же, как и с другими заполненными клетками. Эту фиктивную нулевую поставку можно ставить только в ту свободную клетку, чтобы не образовывался квадрат или прямоугольник с вершинами из заполненных клеток.
Метод Фогеля
Вначале определяют разность между двумя наименьшими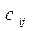 
по строкам и столбцам. Находят наибольшую разницу. В строке (в столбце) с наибольшей разностью заполняется клетка с минимальным 
. Далее повторяем те же действия с не выпавшими клетками.
Покажем на примере, как находится первоначальное базисное распределение поставок методом наименьших затрат.