Прежде всего следует отметить, что релятивистская механика строится на постулатах СТО. Она существенно отличается от классической, Ньютоновской механики. Значит, следует определить основные динамические переменные релятивистской механики.
В механике Ньютона все динамические переменные определены в предположении, что время абсолютно, то есть 
. В релятивистской механике это предположение изначально не принимается. Однако, несмотря на это, динамические переменные следует определить так, чтобы они оставались одинаковыми во всех инерциальных системах отсчета. Следовательно, все они нуждаются в переопределении. Стоит отметить, что некоторые аналогии с классической механикой сохраняются.
В Ньютоновской механике импульс определяется как 
. Необходимо осуществить переход от трехмерного к четырехмерному вектору импульса: 
.
Четырехмерный вектор импульса должен иметь вид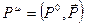 
. Обозначим 
, где 
имеет размерность энергии. Согласно Ньютону, импульс должен быть пропорционален скорости, значит для четырехмерного вектора импульса:
.
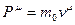- некоторая, пока не определенная инварианта, имеющая размерность массы.
Используя определения четырехмерной скорости, можно записать:
.
Если рассмотреть трехмерную, пространственную компоненту, то:
, где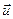 
- Ньютоновская скорость.
Причем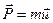 
, а это значит, что 
. Причем, в системе покоя 
. То есть - масса частицы в системе покоя, истинная масса частицы. Масса же 
есть относительная, релятивистская масса, существенно зависящая от скорости при стремлении последней к скорости света.
Обозначенная выше величина может быть определена из тех соображений, что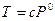 
:
.
В Ньютоновской механике нет аналогии этой величины. Перейдем к нерелятивистскому приближению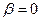 
, чтобы определить физический смысл :
.
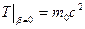Это – формула для энергии покоя, полученная Эйнштейном. Она означает, что покоящаяся частица обладает энергией, которая, например, может частично выделится в процессе распада. Разложим теперь по малым 
:
.
Видно, что второе слагаемое есть не что иное, как кинетическая энергия движущейся частицы. Таким образом, физический смысл состоит в том, что это кинетическая энергия частицы вместе с энергией покоя:
.
Четырехмерный вектор импульса обладает инвариантами аналогично четырехмерному вектору скорости:
.
.
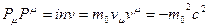Последнее соотношение между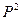 
, 
и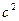 
может быть записано как:
или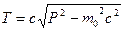 
.
Учитывая то, что 
, получаем, что из инвариантности 
следует энергия в виде:
.
Определим теперь четырехмерный вектор силы. У Ньютона сила есть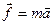 
. В релятивистской механике ему соответствует четырехмерный вектор:
.
В классической механике сила пропорциональна ускорению, значит 
выглядит как:
.
Очевидно, что здесь есть уже определенная выше масса покоя частицы.
Выясним теперь физический смысл нулевой компоненты четырехмерного вектора силы. Из определения видно, что:
.
С другой стороны:
.
Таким образом, можно получить выражение для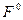 
:
.
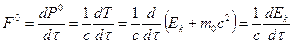(Очевидно, что производная от 
равна нулю.)
Введя буферную производную по 
, получаем:
.
Перейдя теперь к нерелятивистскому приближению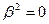 
, имеем:
.
Таким образом, величина 
имеет размерность и смысл мощности:
.
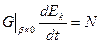К этому соотношению можно подойти с другой стороны, используя ортогональность четырехмерных векторов скорости и ускорения: 
. Получаем:
=> 
.
То есть вектора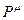 
и также ортогональны в четырехмерном пространстве. Раскроем скалярное произведение:
.
Если теперь использовать определение четырехмерной скорости, получаем:
=> 
=> 
.
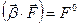Оказывается, что 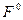может быть выражена через пространственные компоненты. Также важно, что при 
и 
, что означает пространственноподобность четырехмерного вектора силы. Его временная компонента обращается в нуль в системе покоя.
(Кстати, это условие выполняется для любого пространственноподобного вектора. Если вектор 
пространственноподобный, то есть в системе покоя, где , всюду 
, то для него всегда выполняется соотношение 
).
С другой стороны, так как 
, можно записать:
=> 
,
где 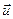- «обычная» Ньютоновская скорость. Несложно показать, что перейдя к нерелятивистскому приближению, мы будем иметь дело с Ньютоновской силой:
.
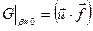Известно, что 
есть мощность 
.