Соотношение  определяет все уравнения движения. Это, собственно, и есть вариационный принцип Гамильтона, гласящий, что вариация действия для истинного движения должно равняться нулю. Следует ввести само понятие действия.
определяет все уравнения движения. Это, собственно, и есть вариационный принцип Гамильтона, гласящий, что вариация действия для истинного движения должно равняться нулю. Следует ввести само понятие действия.
Согласно классической, нерелятивистской механике, действие выглядит как:
 ,
,
где  - функция Лагранжа, описывающая состояние частицы. Таким образом, состояние системы в любой момент времени полностью определяется начальными значениями переменных
- функция Лагранжа, описывающая состояние частицы. Таким образом, состояние системы в любой момент времени полностью определяется начальными значениями переменных  и
и 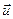 . В этом смысле функция Лагранжа является функцией состояния.
. В этом смысле функция Лагранжа является функцией состояния.
В релятивистской механике такое определение для действия уже не подходит, так как оно не удовлетворяет условию инвариантности вследствие неабсолютности времени. В таких условиях действие должно выглядеть как:
 .
.
Следует оговориться, что функция Лагранжа является инвариантной. Способ построения инвариантной функции Лагранжа будет обсуждена много позже.
Перейдем непосредственно к взятию вариации от «нового» действия.
Для начала вкратце оговоримся, что здесь понимается под вариацией.
В нерелятивистской механике, если заданы истинные координаты  и
и  , заданные таким образом, что между ними возможны различные типы движения, то через них проходит бесконечное количество виртуальных траекторий, среди которых существует только одна истинная, по которой действительно происходит движение. Пусть вторая траектория истинная. Тогда вариацией
, заданные таким образом, что между ними возможны различные типы движения, то через них проходит бесконечное количество виртуальных траекторий, среди которых существует только одна истинная, по которой действительно происходит движение. Пусть вторая траектория истинная. Тогда вариацией  будет множество всех отклонений значений от истинного в данный момент времени (изохронная вариация). Взятие вариации происходит по тем же правилам, что и взятие дифференциала, правда эти понятия различны. Выполняя дифференцирование, аргументу дается приращение и дифференциал есть разность функции для начального и конечного моментов интервала
будет множество всех отклонений значений от истинного в данный момент времени (изохронная вариация). Взятие вариации происходит по тем же правилам, что и взятие дифференциала, правда эти понятия различны. Выполняя дифференцирование, аргументу дается приращение и дифференциал есть разность функции для начального и конечного моментов интервала  . То есть, это приращение, которое получает функция при изменении аргумента на величину
. То есть, это приращение, которое получает функция при изменении аргумента на величину  . Дифференциал не изохронен, а вычисляется для бесконечно малого ненулевого отрезка времени.
. Дифференциал не изохронен, а вычисляется для бесконечно малого ненулевого отрезка времени.
Возьмем вариацию, пользуясь правилами взятия дифференциала:
 .
.
Рассмотрим второй интеграл:


 .
.
В таком случае выражение для вариации действия выглядит как:
 .
.
Так как  является производной, то
является производной, то  . Это означает, что нулю равняется выражение в квадратных скобках. Следовательно:
. Это означает, что нулю равняется выражение в квадратных скобках. Следовательно:
 .
.
Полученное выражение есть уравнение Эйлера-Лагранжа для релятивистской механики. Единственное отличие от нерелятивистского случая заключается в том, что здесь их не три, а четыре.
Заметим, что функция Лагранжа содержит произвол, который заключается в том, что она определяется с точностью до полной производной по времени от произвольной функции.
Вывод силы Лоренца.
Главным объектом для изучения в электродинамике является заряд, находящийся во внешнем электромагнитном поле. Поэтому сила, действующая на заряд со стороны электромагнитного поля, является основной силой в электродинамике. Она называется силой Лоренца.
Сила Лоренца определяет уравнения движения заряда.
Для определения силы Лоренца необходимо задать конкретный вид функции Лагранжа для заряда, находящегося во внешнем поле. Известно, что функция Лагранжа есть функция координат и скорости:  . Более того, известно, что
. Более того, известно, что  . Руководствуясь соображениями простоты изложения, будем вести рассуждения для случая свободной частицы. Функция Лагранжа в таком случае может зависеть от ряда скалярных произведений - инвариант, как то
. Руководствуясь соображениями простоты изложения, будем вести рассуждения для случая свободной частицы. Функция Лагранжа в таком случае может зависеть от ряда скалярных произведений - инвариант, как то  (I),
(I),  (II),
(II),  (III). В первом случае функция Лагранжа зависит от того или иного места в пространстве, то есть нарушается принцип однородности пространства. Во втором случае входит скалярное произведение
(III). В первом случае функция Лагранжа зависит от того или иного места в пространстве, то есть нарушается принцип однородности пространства. Во втором случае входит скалярное произведение  , что приводит к тому, что функция Лагранжа зависит от угла между
, что приводит к тому, что функция Лагранжа зависит от угла между  и
и  , что в свою очередь означает нарушение принципа изотропности пространства.
, что в свою очередь означает нарушение принципа изотропности пространства.
Будем рассматривать случай зависимости функции Лагранжа от инварианта  для случая свободной частицы без внешних полей:
для случая свободной частицы без внешних полей:
 .
.
Запишем соответствующее уравнение Лагранжа:
 .
.
Так как рассматривается случай свободной точки, когда функция Лагранжа не зависит от положения явно, очевидно имеем  и окончательно уравнение Лагранжа запишется как
и окончательно уравнение Лагранжа запишется как

Запишем теперь функцию Лагранжа в явном виде в уравнение и возьмем производную по  :
:
 .
.
Отсюда видно, что в таком случае импульс  и, следовательно, скорость свободной частицы является постоянной величиной.
и, следовательно, скорость свободной частицы является постоянной величиной.
Если же частицу (или заряд) поместить во внешнее поле, то вид функции Лагранжа усложнится. В нее войдут функция Лагранжа  , описывающая движение свободной частицы, и
, описывающая движение свободной частицы, и 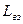 , описывающая взаимодействие частицы (заряда) с полем:
, описывающая взаимодействие частицы (заряда) с полем:
 .
.
Причем, 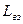 также должна быть инвариантной. Таким образом, общая функция Лагранжа будет выглядеть как
также должна быть инвариантной. Таким образом, общая функция Лагранжа будет выглядеть как
 ,
,
где  есть четырехмерный потенциал. Вообще, потенциал определяет взаимодействие заряда с внешним полем.
есть четырехмерный потенциал. Вообще, потенциал определяет взаимодействие заряда с внешним полем.
В этом случае частные производные функции Лагранжа будут иметь следующий вид:
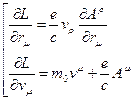 .
.
Здесь  - немой вспомогательный индекс, помогающий избежать путаницы между выходными индексами и индексами, по которым происходит суммирование. И, наконец, уравнение Лагранжа запишется как
- немой вспомогательный индекс, помогающий избежать путаницы между выходными индексами и индексами, по которым происходит суммирование. И, наконец, уравнение Лагранжа запишется как
 .
.
Взяв соответствующие производные и вспомнив, что четырехмерный вектор ускорения есть  , получим:
, получим:
 .
.
Наконец, воспользовавшись тем фактом, что  , запишем
, запишем
 .
.
Выражение слева есть ни что иное как сила, а скобка в правой части есть определения тензора электромагнитного поля  . Таким образом, было получено выражение для силы, являющейся представлением силы Лоренца, которое имеет вид
. Таким образом, было получено выражение для силы, являющейся представлением силы Лоренца, которое имеет вид
 .
.
Найдем теперь компоненты силы Лоренца.
 .
.
Несложно показать, что, например, первая компонента силы Лоренца выглядит как
 ,
,
и, следовательно,
 .
.
Таким образом, четырехмерный вектор силы Лоренца имеет вид
 .
.
Иначе:

В слабом нерелятивистском приближении, то есть в случае, когда  и
и  , выражение для силы Лоренца принимает вид
, выражение для силы Лоренца принимает вид
 .
.
Вторая часть выражения, умноженная на  , представляет собой трехмерный вектор силы Лоренца в нерелятивистском случае.
, представляет собой трехмерный вектор силы Лоренца в нерелятивистском случае.
Нулевая компонента выглядит как
 .
.
Смысл нулевой компоненты заключается в том, что она соответствует закону сохранения энергии в случае стационарных полей. Это можно показать следующим образом: запишем  через потенциал:
через потенциал:
 .
.
Тогда нулевая компонента запишется через
 .
.
Если поле стационарно, то производная  и, следовательно,
и, следовательно,
 .
.
Запишем тогда нулевую компоненту силы Лоренца следующим образом:
 =>
=>
 =>
=>  =>
=>  .
.
Но известно:
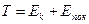 ,
,  ,
, 
Энергия покоя  по определению. Но тогда справедливо
по определению. Но тогда справедливо
 ,
,
что и требовалось показать.