— Так вот, — продолжал Мате, принимая из рук Фило заново наполненный стакан, — вы уже сами установили, что задача об удвоении куба сводится к вычислению корня кубического из двух. На языке современной алгебры, то есть пользуясь буквенными обозначениями, это можно записать так:
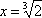
что вытекает из известного еще в Древнем Вавилоне уравнения x3 = 2. Менехм предложил записать это уравнение в виде двойной пропорции:
1/х = х/у = у/2.
— Не понимаю, — сказал Фило, — откуда взялся игрек?
Мате возвел очи к небу. О Господи! Он и забыл, что для Фило алгебраические преобразования — китайская грамота.
— Исключите из этих двух пропорций смущающий вас игрек, и вы снова получите x3 = 2, — объяснил он, доставая блокнот. — Смотрите. Из пропорции 1/х = х/у следует, что у = х2. Подставьте в равенство ху = 2 вместо игрека x2, и получится, что х 3 = 2. Теперь вы видите, что от преобразования, сделанного Менехмом, наше первоначальное уравнение ничуть не изменилось.
— Зачем же было переливать из пустого в порожнее?
— Как — зачем? Да ведь вместо одного уравнения мы получили два: ху = 2 и у = х2.
— Подумаешь, прибыль!
— И очень большая. Потому что ху = 2 — это не что иное, как уравнение равносторонней гиперболы, а у = х2 — уравнение параболы!
— Конические сечения!
— В том-то и дело. И, стало быть, теперь мы можем изобразить наше уравнение в виде кривых на чертеже. Для этого начертим сперва оси координат…
— Чего-чего?
— Оси координат, — раздельно повторил Мате. — Пора о них знать.
— Вот еще! — фыркнул Фило, пылая благородным негодованием. — Мы этого в школе не проходили.
— Не мы, а вы, — уточнил Мате. — Вы не проходили. Но теперь вам от этого не отвертеться. Так вот, достопочтенный Санчо, соблаговолите запомнить, что оси координат существуют для того, чтобы определять положение точки на плоскости или в пространстве. Само собой разумеется, что для нахождения точки на плоскости достаточно двух координат. Если же точканаходится в пространстве, которое, как известно, трехмерно, тут уж потребуются три координаты.
— Ну, это нам ни к чему, — быстро ввернул Фило. — Мы ведь ищем точку на плоскости. Стало быть, хватит с нас и двух координат.
— Прекрасно! — неожиданно похвалил Мате. — Раз вы уразумели это, значит, поймете и то, как строятся графики уравнений. Итак, вычертим оси координат, иначе говоря — две взаимно перпендикулярные прямые. Одну из них — горизонтальную — назовем осью иксов, другую — вертикальную — осью игреков. Точку их пересечения обозначим буквой О. Начнем с уравнения параболы…
— Игрек равняется иксу в квадрате, — сейчас же припомнил Фило.
— Вот именно, — подтвердил Мате. — В чем особенность этого уравнения? А в том, что каким бы ни было числовое значение икса, игрек всегда будет равен квадрату этого числа. Допустим, что икс равен нулю. Тогда игрек равен…
— …тоже нулю, — подхватил Фило.
— Правильно. Вот и найдем эту точку на плоскости.
— А ее искать нечего: вот она! — Фило ткнул пальцем в точку О.
— Совершенно верно. Иначе, точка с координатами ноль, — ноль совпадает с началом координат. Пошли дальше. Допустим, что икс равен единице. Тогда игрек тоже равен единице, так ведь? Найдем точку с координатами единица — единица. Для этого отложим сперва единицу на оси иксов вправо от точки 0…
— В каких единицах длины? — озабоченно перебил Фило.
— В каких угодно. Но для удобства лучше все-таки не в километрах.
— Тогда в сантиметрах?
— Да будет так! Итак, вправо от точки О по оси иксов откладываем один сантиметр. Из конца этого отрезка восстанавливаем перпендикуляр также длиной в один сантиметр. Конец этого перпендикуляра и есть искомая точка с координатами один — один. Допустим теперь, что значение икс не единица, а двойка. Тогда игрек равен…
— Четырем!
— Браво! После этого гениального заявления вам остается лишь найти точку с координатами два — четыре самостоятельно.
Фило отложил два сантиметра от точки О по оси иксов, восстановил из конца этого отрезка перпендикуляр, равный четырем сантиметрам, и посмотрел на Мате победоносно, как актер, ожидающий бурных оваций.
Но оваций не последовало. Мате весьма сухо потребовал, чтобы Фило нашел точку при х = 3, потом х = 4, и отвязался от него только тогда, когда места на листке уже не осталось.
— Ну вот, — процедил он, окинув чертеж критическим оком. — Мы получили несколько точек, удовлетворяющих уравнению у = х2. Все они, естественно, лежат на нашей параболе. Стало быть, остается соединить их плавной кривой — и график данного уравнения, то бишь парабола, перед нами!
Фило недовольно осмотрел вычерченную Мате линию.
— Позвольте, — сказал он заносчиво, — какая же это парабола? Помнится, там, на базаре, вы показали мне кривую, напоминающую рогатку, а тут…
— А тут половина рогатки, — засмеялся Мате.
— Но куда же девалась вторая половина?
— Вторая находится по левую сторону оси игреков, где координаты х отрицательны. А так как отрицательное число, возведенное в квадрат, становится положительным, значит, игрек тоже будет у нас всегда числом положительным. Вот и выходит, что координаты игрек и справа и слева от вертикальной оси совершенно одинаковы. А раз так, значит, левая часть параболы симметрична правой. Дорисуем ее, если хотите, — и целая рогатка в вашем распоряжении. А теперь, когда с параболой покончено, тем же способом вычертим гиперболу, ху = 2.
Фило почесал в затылке. Сразу видно, что тут придется попотеть!
— Почему вы думаете? — осведомился Мате.
— Так ведь в первом уравнении икс и игрек были по разные стороны равенства, а тут в общей куче…
— Раз это вас смущает, отделим их друг от друга. Нетрудно выяснить, что у = 2/х. Заменим первое уравнение вторым — и дело с концом!
— Ага! — кивнул Фило. — Тогда начнем, как полагается, с х = 0…
— Стоп! Как известно, деление на нуль запрещено. Так что начнем с х= 1. Тогда у = 2/1, или попросту двум…
— Значит, находим точку с координатами один — два, — подхватил Фило, орудуя карандашом.
— Дальше.
— Дальше нахожу точку при х = 2. Игрек при этом равен единице. При х = 3 игрек равен двум третям… Постойте, как же так? — Фило запнулся. — Выходит, чем больше икс, тем меньше игрек?
— Правильно подмечено! — одобрил Мате. — Чем больше икс, тем меньше игрек, и обратно: чем меньше будет становиться икс, стремясь к нулю, тем больше будет становиться игрек, стремясь к бесконечности. А теперь соединим, наконец, найденные нами точки одной линией — и гипербола готова.
— К тому же не наполовину, а целиком, — удовлетворенно констатировал Фило. — Точь-в-точь как та, что вы нарисовали в Исфахане.
— Должен вас огорчить. То, что я нарисовал в Исфахане, полной гиперболой не было, как не был полной конической поверхностью и тот бумажный фунтик, который мы с вами рассекали воображаемыми плоскостями. Потому что полная коническая поверхность состоит не из одного, а из двух одинаковых фунтиков, соприкасающихся вершинами. И, стало быть, в каждом из этих фунтиков образуется только одна ветвь гиперболы, в то время как полная гипербола состоит из двух ветвей.
— Значит, на нашем чертеже должна быть еще одна ветвь. Но где же она? — недоумевал Фило.
— Ее нетрудно получить, придавая иксам отрицательные значения. Только, в отличие от параболы, игрек при этом тоже будет принимать не положительные, а отрицательные значения.
— Так, так, так, — озабоченно пробормотал Фило. — Икс отрицательный. Значит, откладывать его следует по оси иксов влево. Но вот вопрос: на какой оси откладывать отрицательные игреки?
— Это уж пустяки. Положительные игреки расположены вверх по оси иксов, стало быть, отрицательные…
— Вниз! — сообразил Фило и принялся откладывать отрицательные координаты точек -1, -2; -2, -1; -3, -2/3 и, наконец, — 1/2, -4. — Теперь, — сказал он, полюбовавшись своей работой, — объединим все это хозяйство общей линией, и вторая ветвь гиперболы налицо. Ура, ура и в третий раз ура! Остается выяснить главное: для чего все это делалось?
— Для того, чтобы понять, каким образом Менехм решал задачу об удвоении куба, — пояснил Мате. — А решал он ее так: изображал обе кривые на одном чертеже, рассматривая при этом только ту часть координатной плоскости, на которой эти кривые пересекаются. Точка пересечения их — обозначим ее буквой А — удовлетворяет и первому и второму уравнениям, а следовательно, и уравнению х2 = 2. Опустим из этой точки перпендикуляр на ось иксов, обозначив основание перпендикуляра буквой В, и искомая нами длина ребра удвоенного куба найдена: это отрезок OB. Ему-то и равен х. Вот как конические сечения помогли Менехму решить одни из видов кубического уравнения. А Хайяму они помогли решить все нерассмотренные до него виды.
— Кажется, он насчитал их четырнадцать, — вспомнил Фило.
— Собственно говоря, в наше время все эти виды сводятся к одному. Да и способ решения изменился. Теперь кубические уравнения решаются по формуле итальянского математика XVI века Кардано.
Фило разочарованно нахохлился. Как же так? Выходит, Хайям трудился впустую? Мате задумчиво помешал ложечкой в стакане.
— В науке ничего не бывает впустую. Ни открытий, ни ошибок. Конечно, трудам Хайяма не суждено было оказать влияние на развитие европейской математики — эта честь досталась ал-Хорезми. Зато они оказали огромное влияние на математиков Востока. Идеи Хайяма были подхвачены и развиты другими, более поздними учеными. Кроме того, не следует забывать, что в некоторых вопросах Хайям произвел настоящую революцию. Достаточно вспомнить его календарную реформу. Или учение о числе… Надо вам знать, что Хайям был первым, кто признал иррациональные числа и, таким образом, открыто выступил против Аристотеля, который во всем остальном оставался для него непререкаемым авторитетом.
Фило недоверчиво поджал губы. Чудно! Неужели было время, когда иррациональных чисел не признавали?
— Было время, когда не признавали и отрицательных, — сказал Мате. — Вот, например, два минус пять. С нашей точки зрения, это можно рассматривать как сложение положительного и отрицательного чисел: 2 + (-5) = -3. С точки зрения древних, такое вычитание невозможно. Уравнение х + 2 = 0, по их мнению, также чистейшая нелепость, ибо нет такого числа, которое, будучи прибавлено к двум, равнялось бы нулю. А по-нашему, такое число есть: это -2. Поэтому уравнение вполне разрешимо. Просто корень у него отрицательный.
Фило вдруг зажмурился. Подумать только, сколько отчаянного труда, смелости и немыслимого таланта стоит за любым, самым, казалось бы, незначительным научным понятием! Это похоже на бесконечную лестницу, где каждая ступенька штурмуется как горный пик. Чтобы признать какое-то безобидное иррациональное число, Хайям должен был обладать мужеством богоборца: ведь он посмел оспаривать самого Аристотеля! А Эратосфен, дерзнувший ввести движение в геометрию, вероятно, чувствовал себя чуть ли не преступником…
— Кстати, об Эратосфене, — круто свернул в сторону Фило. — Мне кажется, ему непременно следовало бы изменить имя.
— Это еще зачем?
— Судите сами: Эрато в Древней Греции — муза любовных песен. Разве это подходит математику? Вот если бы Эратосфен писал стихи…
— К счастью, он их не писал, — безапелляционно заявил Мате.
— Вы уверены? После истории с двумя Хайямами я бы на вашем месте не слишком полагался на свою память.
Мате покраснел. Проклятая забывчивость! Он снова направился в прихожую и вернулся с книгой в черном глянцевом переплете.
— Вот, — сказал он, — здесь собраны биографии ученых Древнего Вавилона, Египта, Греции. Сейчас открою главу об Эратосфене и выясню, чего я там не заметил.
— Позвольте мне! — Фило осторожно отнял у него книгу.
Он мгновенно, как всегда, нашел нужную страницу, пробежал ее глазами и торжествующе рассмеялся.
— Так и есть! «Он (то есть Эратосфен) был знаменит во многих отраслях: как математик, географ, историк, филолог и поэт. Образчиком его тонкого стихотворного искусства является эпиграмма об удвоении куба… В его диалоге „Платоник“ рассматривается не только эта делийская задача, но и философские проблемы и некоторые вопросы теории музыки. Он написал поэму о звездном небе в форме повествования о небесных странствиях Гермеса[20]и его всевозможных приключениях, а также собрал мифы, касающиеся созвездий. Он составил новую карту мира, основанную на предположении шарообразности Земли, вычислил наклон эклиптики,[21]расстояния до Солнца и Луны и длину земного меридиана. И он же написал большое исследование о древнегреческой комедии… Кроме того, Эратосфен считается родоначальником критической хронологии, так как научил человечество точно определять даты исторических событий…» Ну, что скажете?
— Скажу, что Эратосфену незачем менять имя, — угрюмо буркнул Мате. — И еще, что вы как филолог-любитель должны были знать о существовании такого интересного литератора.
— Должен был знать и узнал. Но вы не сказали самого главного. Мы с вами то и дело натыкаемся на примеры, свидетельствующие о губительной, тормозящей силе предубеждений, а между тем со своими собственными предубеждениями расстаемся весьма неохотно.
— Да, это вам не чай пить, — довольно язвительно отозвался Мате.
— Согласен. Но на то мы и друзья, чтобы помогать друг другу преодолевать трудности. Как это сказал тогда Хайям? «Что видно на другом, то на себе не видно. Дурные стороны видней со стороны…»
— Иначе, вы мне будете помогать избавляться от моих предубеждений, а я вам от ваших, — уточнил Мате. — Что ж, по рукам!
Они обнялись, но тут за стеной раздались душераздирающие вопли. Фило и Мате бросились в кухню: Клеопатра и Пенелопа тузили друг друга почем зря! Мате хотел разогнать их, но Фило, улыбаясь, увел его обратно в комнату. Кто знает, может быть, они избавляют друг друга от предубеждений?
ЧАСТЬ ВТОРАЯ
Числа и кролики
У ГОРОДСКИХ ВОРОТ
— Мате!
— Хррр…
— Мате, проснитесь!
Мате блаженно почмокал губами.
— Успеется, Фило… Еще рано.
— Какое там «рано»! Четверть тринадцатого.
— Что?! — Мате вскочил, испуганно моргая заспанными глазами. — Тринадцатый час?
— Тринадцатый век. Тысяча двести двадцать пятый год.
— Вот это да!
Их окружала безлюдная сельская местность. Хмурое утро освещало синеватые затуманенные горы и нищие, крытые соломой лачуги. Мате зябко передернул плечами. Не больно здесь тепло… Куда это их занесло? Уже не в Скандинавию ли?
— Скажите еще на Северный полюс! — проворчал Фило. — В марте, да еще по утрам, холодно бывает и в Италии.
Мате удивленно свистнул: так они в Италии! Где же именно? Фило укоризненно покачал головой.
— У вас не память, а решето Эратосфена. Не вы ли с пеной у рта уговаривали меня отправиться в город Пизу, чтобы разыскать там какого-то малоизвестного математика со странным именем Фибоначчи?
Мате, как всегда в таких случаях, смущенно потер лоб. Хорошо, что ему напомнили! Но с чего это Фило взял, что Фибоначчи мало известен?
— Странный вопрос! — Фило высокомерно выпятил нижнюю губу. — О нем в энциклопедии ровным счетом четыре строчки.
— Предубеждение номер один! — отметил Мате. — Интересно, сколько строчек останется в энциклопедии после вас?
— Грубо, грубо и в третий раз грубо.
Глаза у Мате сузились и стали совсем враждебными. А разве не грубо судить об ученом только потому, сколько почестей воздано ему в энциклопедии? Да знает ли Фило, что такое Фибоначчи? Это же основоположник новой эры в европейской математике! Да, да, эры, и ни на миллиметр меньше! Фибоначчи был тем самым человеком, который познакомил Европу с великой математикой средневекового Востока. Это благодаря ему здесь узнали о десятичной системе счисления. Да если бы не Фибоначчи, человечество, может быть, до сих пор пользовалось бы неуклюжими римскими цифрами или — страшно сказать! — какой-нибудь вавилонской клинописью.
Фило равнодушно пожал плечами.
— Ну и пусть. Мне-то что?
— Конечно, — напустился на него Мате, — вы же у нас филолог, счетом не занимаетесь. А ведь еще Чехов сказал: «Специалист подобен флюсу: полнота его односторонняя».
— С вашего разрешения, это сказал не Чехов, а Козьма Прутков.
— А что от этого меняется? Ваш флюс как был, так и остался при вас.
— А ваш — при вас. И при вашем Фибоначчи.
— Черт знает что! — вышел из себя Мате. — Так говорить об авторе знаменитой «Либер абачи»!
— «Либер абачи», — повторил Фило. — Если не ошибаюсь, учебник арифметики?
— Вот именно, и, смею вас заверить, замечательный, — с жаром подхватил Мате. — Среди математических книг того… простите, этого времени нет ему равных! Необычайное богатство и разнообразие задач, доказательность, оригинальные методы решений — все это сделало «Либер абачи» интересной и полезной не только для тех, кто изучает математику в практических целях, но и для настоящих ученых. Неспроста удивительная книга Фибоначчи стала источником, из которого черпали многие математики последующих столетий! Задачи и приемы решений «Либер абачи» встречаются в трудах итальянских, немецких, английских, французских, русских математиков. Их можно обнаружить даже в произведениях восемнадцатого века! А так называемые числа Фибоначчи? Да ведь им нет цены! Долгое время они оставались забытыми. Но теперь! О, теперь Фибоначчи и его числа известны всему просвещенному человечеству…
Мате говорил так искренне, с таким увлечением, что Фило невольно растаял.
— Хорошо, хорошо, сдаюсь. Ваш Фибоначчи — гений. Но лучше один раз увидеть, чем сто раз услышать.
— Вот это верно! Мы сейчас же отправляемся на розыски.
— Прежде надо еще войти в город, — возразил Фило, указывая куда-то направо.
Мате повернул голову. Шагах в двухстах от них простиралась бесконечная крепостная стена. Тяжелые, обитые железом ворота были закрыты. У караульной башни прохаживались двое стражников с алебардами. Мате заметил, что маленькая сводчатая дверь башни приотворена.
— Все в порядке, — сказал он. — Башня наверняка служит проходной. Одна минута — и мы в городе.
— Так нас и пустят!
— Конечно, пустят. Мы же невидимки!
— Вы думаете, поэтическая шутка Хайяма сработает и на сей раз? А если не сработает?
— Рискнем.
— Э, нет! — запротестовал Фило. — Не желаю быть вздернутым на виселицу в качестве генуэзского лазутчика.
— Почему же непременно генуэзского?
— Следовало бы вам знать, что Генуя и Пиза — отчаянно конкурирующие морские державы. Они постоянно строят друг другу козни. Пройдет каких-нибудь шестьдесят лет, и Генуя нанесет Пизе удар, от которого ей уже никогда не оправиться. Пизанский флот будет разбит, авскоре Генуя в союзе с другими итальянскими городами нападет на Пизу с суши…
Мате ревниво заметил, что Фило неплохо подготовился к путешествию. Только с чего он взял, что Пиза — морская держава? Ведь она, кажется, стоит на реке Арно, а Генуэзский залив расположен в двенадцати километрах от города.
— Так-то оно так, — сказал Фило, — но не забывайте, что сейчас, в тринадцатом веке, Арно еще судоходна — и корабли из Генуэзского залива поднимаются до самого города.
Мате вздохнул:
— Они-то поднимаются, а мы… Ну да ладно, сейчас что-нибудь придумаем. Видите плетеную изгородь? Ту, недалеко от стены? Подберемся к ней ползком, заляжем, а там улучим удобную минуту и — в башню!
Фило огорченно посмотрел на свои опрятные бумажные брюки, заменившие на сей раз шорты. Бедные джинсы, за пять лет он так с ними сроднился! Но, как поется в старинной венгерской балладе, еще больше было потеряно на Могашском поле…
Он отважно лег животом на холодную землю и, сопя от усердия, пополз. Мате сделал то же самое, и скоро они благополучно добрались до плетня, за которым раздавались грубые голоса стражников.
— Опять всю ночь выли волки, — сказал один.
— Совсем обнаглели, — отвечал другой. — И развелось же их! Пропасть…
— Немудрено. Убивать-то некому…
— Твоя правда. Прежде как было? Люди охотятся, звери прячутся в норы. Нынче звери рыщут в поисках добычи, а люди забились в свои норы и боятся нос наружу высунуть.
— Побоишься тут, когда от разбойников спасенья нет. Вот и на соседнюю деревню тоже напали.
— Да что ты!
— Не сойти мне с этого места. Стариков поубивали, остальных — в рабство. О скотине и не говорю: лошадей, ослов, свиней — всех угнали.
— Этак скоро все мы с голоду перемрем, — сокрушался второй. — Некому станет ни сеять, ни жать, ни возделывать виноградники. Если крестьяне где еще и работают, так только в пригородах. Да и то под вооруженной охраной… А все проклятые раздоры!
— Да, чего-чего, а этого добра у нас хватает. Кто только у нас не враждует! Города, провинции, семьи. Только и слышишь: осады, пожары, сражения…
— Что ж удивляться, если и верховные-то наши владыки — Папа с императором — и те дерутся не на жизнь, а на смерть. А кто из них прав, кто виноват? Поди разберись…
— Но-но-но! — неожиданно ожесточился первый. — Ты, может, не разберешься, а я разберусь.
— Это почему же?
— Потому что я чистокровный пизанец. Стало быть, гибеллин[22]и сторонник императора. А твоя мать откуда родом?
— Ну, из Болоньи, — неохотно буркнул второй.
— Ага! Выходит, пизанец ты только наполовину. А болонцы — они все до единого гвельфы и паписты. Это уж как пить дать.
— Ну и что? Еще неизвестно, кто лучше: Папа или император. Папа хоть христианин, а император…
— Что — император? — горячился первый. — Ну, договаривай!
— Антихрист он, вот что.
— Да как ты смеешь! — зарычал первый, лязгая мечом в ножнах. — Говорят, наш государь, Фридрих Второй, получил корону не от Папы, а от самого Господа Бога. А уж Бог антихриста нипочем императором не сделает.
— Отчего же тогда твой Фридрих отлынивает от крестового похода? — продолжал наступать второй. — Отчего при дворе у него в почете иудеи и сарацины?[23]Молчишь? То-то. И потом, антихрист — он ведь должен быть сыном дьявола и монахини. Так ведь?
— Та-а-ак…
— А мать императора, эта сицилийка Констанция, до того как ей выйти за короля Генриха, говорят, и была монахиней. Значит, как ни верти, а все сходится.
Сраженный этим неопровержимым доказательством, первый не нашел, что ответить, и товарищ его, очень довольный своей победой, продолжал разглагольствовать. По его словам, гвельфы и гибеллины произошли от двух дьяволов — Гвелефа и Гибела, посланных из ада на землю, чтобы истребить человечество нескончаемыми войнами.
Мате чуть не фыркнул, слушая эту галиматью, но Фило вовремя ущипнул его за ногу: ничего смешного! Средневековье — время бескультурья, бездорожья и разобщенности. Неудивительно, что здесь процветают самые нелепые, самые чудовищные слухи.
От шепота его у Мате так защекотало в ухе, что он снова чуть было не фыркнул… Вдруг вдали послышалось заунывное пение. Друзья обернулись и увидели, что к крепостной стене движется нечто черное и бесформенное, какая-то стелющаяся по земле поющая туча. По мере того как туча приближалась, пение становилось все громче.
— Смотри-ка, Фило, да это люди!
Да, то были люди, хотя, скорее, их можно было принять за толпу призраков. Изнуренные, босые, в черных балахонах с красными крестами на груди, они шли, держа в руках ветки и зажженные свечи. Многие были опоясаны цепями или толстыми веревками, длинными концами которых время от времени наносили себе жестокие удары.
— Мира! Мира! — пела толпа. — Господи, дай нам мира!
— Что за изуверство! — возмутился Мате. — Зачем они калечат себя?
— Наверное, думают, что войны посланы им в наказание за какие-то грехи, и хотят замолить свою вину перед небом.
— Бедняги! Видно, крепко их допекло… Смотрите, среди них дети?!
Лицо Мате исказилось от жалости, и Фило впервые подумалось, что у этого язвительного человека доброе и легко ранимое сердце.
Тем временем в крепости тоже заметили бичующихся и стали готовиться к встрече. На верхнюю площадку зубчатой стены высыпали солдаты. Холодным сумрачным блеском заиграли на свету металлические каски и нагрудники.
Когда солдаты построились в длинную шеренгу, на стене появился человек с жестким, словно высеченным из камня лицом.
— Наверное, военачальник, — шепнул Фило, — доспехи у него побогаче, чем у других.
Человек подошел к самому краю стены и негромко спросил, обращаясь к толпе:
— Эй, вы, зачем пожаловали?
Слова его, тяжелые и отрывистые, казались такими же каменными, как он сам.
Из толпы, которая успела уже почти вплотную приблизиться к воротам, выступил старик с безумными, запавшими глазами.
— Впусти нас в город! — истошно закричал он, простирая руки. — Пусть жители Пизы присоединят свои голоса к нашим. Может быть, тогда Господь услышит нас и ниспошлет нам мир.
— Впусти нас, впусти! — завыла толпа.
— Назад! — зычно скомандовал человек на стене. — Поворачивайте, пока я не приказал забросать вас камнями. В Милане для острастки таких, как вы, воздвигли шестьсот виселиц. Мы, пизанцы, милосерднее: мы подросту перебьем вас, как сусликов.
Но не так-то легко напугать людей, доведенных до крайности. Обезумевшая толпа ринулась к воротам, исступленно молотя по ним кулаками, в кровь разбивая лбы о кованое железо. Самое примечательное, что никто из этих ослепленных отчаянием страдальцев и не подумал воспользоваться открытой дверью караулки. Не то — наши приятели!
— Теперь или никогда! — сказал Фило. — В башне сейчас наверняка никого нет: гарнизон наверху. Все внимание сосредоточено на толпе.
— Уйти, ничего не сделав для этих несчастных? — заколебался Мате.
— Но что мы можем? Позвонить по телефону в двадцатое столетие и вызвать наряд московской милиции?
— Ваша правда, — мрачно согласился Мате.
Они покинули свое укрытие и ползком добрались до двери. Как и предполагал Фило, караулка, напоминавшая внутренность круглого каменного колодца, была пуста. На грубых дощатых столах в беспорядке валялись игральные кости, опрокинутые второпях глиняные кружки… А вот и дверь в город!
Фило потянул на себя массивное позеленевшее кольцо. Тяжелая, обитая железом створка со скрипом поехала внутрь.
— Добро пожаловать в Пизу, Мате!
Они вышли из башни, и сейчас же по ту сторону стены послышались вопли и стоны вперемешку со звуками, похожими на дробный топот копыт. Это солдаты обстреливали безоружную толпу камнями.
УТРЕННЯЯ ПРОГУЛКА
Они шли по извилистым, отороченным узкими галерейками улочкам, мимо пустынных покуда торговых рядов с запертыми лавками и надменных, обособленных кварталов пизанской знати. Город только еще просыпался, распахивая ставни и скрежеща отодвигаемыми засовами.
Где-то на втором этаже отворилось забранное узорной решеткой оконце, оттуда выглянула одутловатая физиономия в надвинутом на уши ночном колпаке. Потом физиономия исчезла. Вместо нее в окне появилась деревянная лохань, и на середину улицы хлынули помои. Фило и Мате едва успели отскочить.
— Что за свинство! — негодовал Мате. — Не понимаю, куда смотрит санитарная инспекция?
Фило снисходительно пожал плечами. Ничего не поделаешь, средневековье! Жаль, что они не захватили зонтов…
Появились первые прохожие. Пришпоривая богато убранного коня, в туче пыли проскакал нетерпеливый всадник. Перья на его шляпе вскипали, как мыльная пена.
Мате вынужден был признать, что всадник выглядит весьма эффектно. Впрочем, их, вероятно, ждут зрелища более живописные. Выезд императора, например…
Фило посмотрел на друга с покровительственной усмешкой. Вряд ли Фридрих Второй находится в Пизе! Скорей всего, блаженствует в своей любезной Сицилии.
— Почему же в Сицилии? — удивился Мате. — Ведь он, кажется, король Германии?
— Германию он унаследовал от отца, Генриха Шестого Гогенштауфена, а Сицилию — от матери, принцессы Констанции.
— А, это от той, что была до замужества монахиней, — вспомнил Мате.
— Фи, фи и в третий раз фи! Охота вам повторять россказни невежественного солдата. Может, скажете еще, что Фридрих — антихрист?
— Ну нет! — засмеялся Мате. — Это небось измышления папистов? Представляю себе, как он им насолил…
— Так насолил, что через два года его даже отлучат от церкви.
— В таком случае, ваш Фридрих — личность незаурядная.
— Смеетесь? А он, между прочим, и в самом деле человек недюжинный. Я бы даже сказал, необычайный. Император-филоматик. Обладатель замечательной библиотеки. Знаток многих языков. Сочинитель книг об охоте и по уходу за лошадьми. Автор нескольких песен. При дворе его собираются знаменитые ученые разных вероисповеданий и национальностей, и нет науки, которой бы он не интересовался. А в тысяча двести двадцать четвертом… виноват, в прошлом году он даже основал университет в Неаполе.
— Что?! — изумился Мате. — Фридрих основал университет? Значит, он непременно пригласил туда Фибоначчи!