— Три, пять, восемь, тринадцать… Снова числа Фибоначчи! — всплеснул руками Фило.
А Мате продолжал ошеломлять своих слушателей новыми сведениями. Оказывается, с числами Фибоначчи связано расположение листьев на ветке, строение цветка, количество спиралей, образованных семечками подсолнуха, чешуйками ананаса или сосновой шишки…
Дети слушали как зачарованные. Подумать только, папиными числами пользуется сама природа!
Леонардо задумчиво покусывал палец. Трудно было понять, поверил ли он предсказаниям Мате, но мысль, что открытие его, может быть, действительно принесет пользу далеким потомкам, не могла не взволновать его, а рассказ о свойствах чисел Фибоначчи подхлестнул его воображение.
Кто ведает, сколько еще неизвестного и неожиданного таится в этом удивительном числовом ряду!
— Много, дорогой маэстро, — заверил его Мате, слышавший эти последние, произнесенные вслух слова. — Так много, что когда-нибудь о числах Фибоначчи будут написаны целые книги.
Леонардо мечтательно вздохнул. Хотел бы он прочитать хотя бы одну! Мате с досадой подумал о книге, которую по забывчивости оставил на подоконнике московской квартиры. Как бы она сейчас пригодилась!
Чтобы заглушить угрызения совести, он решил познакомить мессера Леонардо с шуточной задачкой, основанной на одном любопытном свойстве чисел Фибоначчи.
Попросив влажную тряпку, Мате хорошенько вытер стол (совсем как классную доску!) и принялся чертить квадрат, разделенный на множество клеток. Но ему не пришлось довести свою работу до конца: в дверь дома отрывисто постучали.
— Магистр Доменик, магистр Доменик! — радостно защебетала Лаура. — Он всегда так стучит!
Дети побежали открывать и вернулись, ведя за руки человека в длинной складчатой мантии, с квадратной шапочкой на черных с проседью волосах. Одежда его весьма напоминала ту, которую видели Фило и Мате на карнавальных горе-лекарях. На том, однако, сходство и кончалось.
Магистр Доменик производил впечатление человека умного и доброжелательного. У него были толстые насмешливые губы и проницательные черные глаза, которые с любопытством уставились на незнакомцев. Узнав, что в гостях у мессера Леонардо математик, он был приятно удивлен, но тут же озабоченно посетовал на то, что побеседовать сейчас им не придется: в Пизу неожиданно прибыл император Фридрих Второй, и ему, Доменику Испанскому, поручено срочно привести Леонардо во дворец, чтобы представить августейшему монарху.
Невероятная новость переполошила всех, кроме того, кого более всего касалась. Леонардо встал и заявил, что готов идти хоть сейчас.
— Как?! — остолбенел магистр. — В таком-то виде?
Спохватившись, Фибоначчи оглядел свою блузу. Да, да, ему, вероятно, следует переодеться…
— И как можно скорее, мой друг, — внушительно сказал Доменик, выпроваживая его из комнаты. — А вы что стоите? — обернулся он к детям. — Ступайте помогите отцу. Да последите, чтобы он не надел чего-нибудь наизнанку.
В следующее мгновение все в доме были заняты делом. Леонардо одевался. Дети метались по комнатам, открывая сундуки и подавая отцу то одно, то другое. Доменик ждал, нетерпеливо барабаня пальцами по столу и повторяя про себя заготовленную для императора латинскую речь. А Фило и Мате мучительно ломали головы над тем, как бы им тоже попасть во дворец, чтобы взглянуть хоть одним глазком на редкую разновидность императора-филоматика и услышать, как он предложит мессеру Леонардо должность в Неаполитанском университете, ибо теперь они уже не сомневались, что его пригласили именно для этого.
Смятение друзей не укрылось от наблюдательного магистра. Узнав, что они хотят видеть церемонию представления, он вызвался помочь им. Император, насколько ему известно, прибыл в Пизу инкогнито, стало быть, прием будет неофициальный, скорее всего в кабинете. Камердинер Фридриха — знакомый Доменику араб — проведет их на балкон, выходящий в кабинет из другой комнаты, а там… Словом, жаловаться на судьбу им не придется!
В приливе благодарности Мате и Фило чуть не оторвали ему руки. Но тут, на его счастье, появился Леонардо в чем-то синем, бархатном, перечерченном тяжелой цепью, которая заканчивалась круглым медальоном размером с доброе блюдце.
Теперь Фибоначчи уже не походил на садовника, но видно было, что он давненько не надевал своего парадного костюма и порядком отвык от него. Фило даже подумал, что блуза, пожалуй, идет ему больше. Зато дети смотрели на отца с восхищением. Он крепко обнял их, по очереди нагибаясь к каждому, и, наказав не ждать его скоро, вышел из дому. Остальные последовали за ним.
В ТАЙНИКЕ
По дороге магистр Доменик осторожно подготовил Леонардо к тому, что представление состоится в присутствии известных ученых. Наверняка будет философ императора, достопочтенный магистр Иоанн из Палермо, а также придворные астрологи Микаэль Теодор и шотландец Микаэль Скотт. Кроме того, император желает познакомиться не только с самим Леонардо, но и с его математическим искусством. Так что пусть маэстро не удивляется, если ему предложат решить несколько задач.
Подобное сообщение хоть кого озаботит, но Фибоначчи, услыхав его, облегченно вздохнул.
— Благодарю вас, дорогой магистр! — сказал он. — Всегда от вас услышишь что-нибудь ободряющее. Признаться, я не очень приспособлен для придворной беседы. То ли дело математика…
Тут он заметил шествующих с ним рядом Фило и Мате и дружески им улыбнулся: вот хорошо-то! Оказывается, их тоже пригласили к императору. Но отчего магистр разрешил им остаться в прежней одежде, а его, Леонардо, заставил переодеться? Право же, в этом бархатном облачении он чувствует себя как в тисках…
Но вот они подошли ко дворцу, который Фило упорно именовал на итальянский лад палаццо.
По правде говоря, нашим филоматикам не очень-то верилось, что великолепный план магистра удастся. Доменик, однако, сказал несколько слов часовому, и их беспрепятственно пропустили. А скоро перед ними возник человек в белоснежном арабском одеянии, с тяжелыми, полуопущенными веками и лицом до того неподвижным и бесстрастным, что при взгляде на него становилось не по себе.
«Прямо истукан какой-то», — подумал Мате.
Доменик пошептал что-то истукану на ухо. Тот движением руки пригласил путешественников следовать за собой, и на некоторое время они оказались разлученными и с Фибоначчи, и со своим нежданным покровителем.
Они пошли по дворцовому лабиринту, скользя по гладко отполированным каменным плитам, где, как в темной воде, двигались их опрокинутые отражения. Любопытные филоматики нет-нет да останавливались, чтобы рассмотреть высокий мавританский светильник или громадный, во всю стену, гобелен, на котором грозно скалились разъяренные львы и круто изгибали породистые крупы вздыбленные арабские скакуны. Но истукан, не оборачиваясь, всякий раз чувствовал это и повелительным жестом приказывал им идти дальше.
Напоследок, поднявшись вслед за своим невозмутимым провожатым по узкой витой лестнице, они очутились в каком-то закутке, завешанном со всех сторон плотными занавесками. Это и был обещанный Домеником балкон. Истукан указал им на две прорези в драпировках, приложил на прощание палец к губам и бесшумно удалился, а Фило и Мате занялись наблюдениями.
Кабинет императора, пока еще безлюдный, был обставлен в восточном вкусе, и Фило подумалось, что молва неспроста обвиняет Фридриха в тайном магометанстве…
Но в это время двери, находившиеся в противоположных концах зала, одновременно распахнулись и впустили с одной стороны Леонардо, Доменика и еще нескольких людей в таких же, как у магистра, мантиях и шапочках, с другой — человека лет тридцати в светло-коричневом замшевом костюме и замшевых же, высоких, чуть не до бедер, сапогах.
Светлолицый, с белокурыми, до плеч, преждевременно поредевшими волосами, император сразу же с любопытством уставился на Фибоначчи, нетерпеливо внимая высокопарной латыни Доменика. Леонардо же, казалось, и вовсе не слушал, и, пока Фридрих изучал его, он, в свою очередь, сосредоточенно рассматривал стоявшую на треножнике серебряную чашу, над которой вилась струйка сладковатого дыма.
— Кажется, вам понравилась эта курильница, — с улыбкой обратился Фридрих к Леонардо, как только Доменик умолк. — Редкая вещь, не правда ли?
— Замечательная, ваше величество, — отвечал Леонардо. — Но дома у меня есть другая, так та, пожалуй, еще лучше.
Фило просто в ужас пришел от его бесцеремонности. К счастью, Фридрих оказался гораздо терпимее.
— Приятно слышать, — сказал он, — что красота чисел не мешает вам, мессер Леонардо, ценить красоту вещей. Мне говорили, у вас замечательная коллекция восточных редкостей. Но… откровенность за откровенность. Я прибыл в Пизу, чтобы познакомиться с редкостью, имя которой Фибоначчи.
— Ваше величество дает мне понять, что пора начать испытание? — спросил Леонардо.
Фридрих слегка поморщился.
— Скорее, урок, — возразил он. — Урок, преподанный императором математики императору-математику.
Леонардо молча наклонил голову. Фридрих любезно осведомился, на чем он предпочитает производить вычисления: на доске или на пергаменте? Тот нерешительно огляделся.
— Дома, занимаясь с детьми, я пишу мелом на столе. Но здесь…
Фридрих не дал ему закончить, быстрым движением указав на длинный стол черного дерева.
— Устраивает вас этот?
— Вполне, ваше величество.
— Прекрасно! Остается условиться о порядке нашего собеседования. Кто будет задавать вопросы мессеру Леонардо? Вы, магистр Иоанн?
Магистр Иоанн, низкорослый, щуплый, с глубоко запавшими беспокойными глазами, высоко вздернул широкие, сросшиеся на переносице брови, похожие на вырезанную из черного бархата птицу. Его величество, сказал он, не раз оказывал ему честь своим доверием. Но вправе ли он, магистр Иоанн, принять столь высокие полномочия на сей раз? Не лучше ли, чтобы вопросы по очереди задавал каждый из присутствующих?
Фридрих беззвучно ему поаплодировал.
— Браво! Этак и на мою долю кое-что останется, — добавил он шутливо и жестом пригласил всех садиться. — Итак, с чего начнем? — спросил он, откинувшись в кресле и удобно скрестив свои длинные замшевые ноги. — Я полагаю, с самой древней и самой заслуженной из всех наук — с арифметики. Кому угодно задать вопрос?
— Позвольте мне, ваше величество, — сказал Доменик, вставая. — Попрошу мессера Леонардо представить число 10 в виде суммы четырех слагаемых так, чтобы каждое из них, начиная со второго, было в два раза больше предыдущего.
В глазах у Леонардо появилось знакомое уже нашим филоматикам отсутствующее выражение, пальцы его рассеянно теребили тяжелые звенья нагрудной цепи. Но не прошло и полминуты, как четыре слагаемых — 2/3, 4/3, 8/3, 16/3 — были названы, и присутствующие благосклонно зашептались.
— Правильность ответа очевидна, — сказал Фридрих, — но, дорогой маэстро, нам хотелось бы знать, как удалось вам найти его столь быстро?
— Очень просто, ваше величество. Для начала я произвольно выбрал четыре числа, каждое из которых вдвое больше предыдущего. И так как всегда удобнее начинать с единицы, остановился на числах 1,2,4,8.
— Однако сумма этих чисел равна не десяти, а пятнадцати, — флегматично заметил громоздкий рыжеволосый человек, чем-то похожий на бульдога и потому вызывавший у Мате безотчетную симпатию.
— Магистр Микаэль Скотт совершенно прав, — подхватил Леонардо. — Потому-то я называю этот способ методом ложного предположения. А так как 10 составляет две трети 15, мне остается умножить каждое из выбранных мною чисел на 2/3, и ответ готов.
— Вот так способ! — зашипел Фило. — Эдак и я могу предположить все, что угодно. Но всегда ли это приведет к правильному ответу?
— Шшш, не мешайте слушать, — оборвал Мате, заметив, что с места поднимается его любимец.
Задача, заданная Скоттом, была также арифметической. Он предложил мессеру Леонардо найти такое наименьшее число, которое при делении на 2, 3, 4, 5 и 6 дает в остатке 1, но при этом делится без остатка на 7.
Фибоначчи успел к этому времени окончательно закрутить свою цепь и занимался тем, что старательно ее раскручивал.
— Не повторить ли вопрос? — улыбнулся Фридрих, просвечивая Леонардо влажными, чуть навыкате глазами. — Я вижу, маэстро распутывает другую задачу.
— Нет, ваше величество, — невозмутимо возразил тот, — ответ 301.
— Непостижимо! Но какой магией пользовались вы в этом случае?
— Всего лишь логическим рассуждением, ваше величество. На сей раз я шел не от ложного, а от обратного предположения. Вместо того чтобы искать число, которое при делении на 2, 3, 4, 5 и 6 дает в остатке 1, я стал искать другое, которое делится на все эти числа без остатка, — попросту их общее наименьшее кратное. Таким наименьшим кратным будет произведение 3, 4 и 5, то есть число 60, которое безусловно делится также и на 2 и на 6. Прибавим к 60 единицу, и задача решена, но… только наполовину. Потому что число 61, к сожалению, не делится без остатка на 7. Следовательно, надо искать число, кратное 60, которое при делении на 7 дает в остатке 6. Таким числом будет 300, то есть 60, умноженное на 5. Прибавим к нему 1, и искомое найдено. Ибо 301 делится без остатка на 7 и в то же время дает в остатке 1 при делении на 2, 3, 4, 5 и 6. Вы удовлетворены, ваше величество?
— Совершенно, — сказал тот. — Мне остается лишь пожалеть о том, что вы предпочитаете считать в уме и потому пренебрегаете моим столом. Сейчас, однако, я предложу такую задачу, что без стола вам не обойтись. Вот она. Из Пизы в Рим отправились 7 старух, а старухи, как известно, запасливы. Каждая вела за собой 7 ослов. На каждом осле было навьючено по 7 мешков, в каждом мешке лежало по 7 хлебов. Сверх того, для каждого хлеба старухи захватили по 7 ножей, а для каждого ножа запасли по 7 ножен. Благоволите сосчитать, сколько всего предметов, включая, разумеется, старух и ослов, отправилось в Рим.
— Нечто подобное я уже слышал. Но где? Убейте, не помню! — шепнул Мате, когда император кончил и все, кроме Леонардо, одобрительно заулыбались.
Фибоначчи тем временем сосредоточенно размышлял, затем открыл было рот для ответа, но, взглянув на Фридриха, передумал и взял мелок
— Ваше величество, — сказал он, в задаче названо шесть разного рода предметов: старухи, ослы, мешки, хлебы, ножи и ножны. Число предметов каждого последующего рода больше предыдущего в семь раз. Стало быть, ответ сводится к сумме следующих шести чисел:
7 х 1= 7
7 х 7 = 49
49 x 7 = 343
343 х 7 = 2401
2401 х 7 = 16807
16807 х 7= 117 649
137 256
Решить эту задачу в уме таким способом действительно сложно, — продолжал Леонардо, — так как при этом надо удержать в голове шесть чисел. Но есть другой способ, позволяющий вычислить результат мысленно, не напрягая памяти. Именно им я и воспользовался. Сначала я нашел число предметов, принадлежащих только одной старухе, включая, конечно, и ее самое. Прежде всего у старухи было 7 ослов. Стало быть, беру 7, прибавляю сюда саму старуху, то есть 1, и получаю восемь: 7 + 1 = 8. Далее нахожу общее число ослов и мешков. У каждого осла было 7 мешков. Вместе с самим ослом это составляет 8 предметов. А так как ослов 7, умножаю 8 на 7 и прибавляю сюда 1 — все ту же старуху: 8 х 7 + 1 = 57. Точно так же поступаю и дальше, каждый раз умножая полученную сумму на число вещей следующего вида и не забывая при этом о старухе: 57 х 7 + 1 = 400; 400 х 7 + 1 = 2801; 2801 х 7 + 1 = 19608. Остается умножить последнее полученное число на 7, то есть на число старух, чтобы получить знакомый уже вашему величеству результат: 137256.
Видимо, второе решение произвело большое впечатление, особенно на Фридриха.
— Мессер Леонардо верен себе, — сказал он, обращаясь к присутствующим. — Он нашел-таки способ обойтись без стола, и, право же, куда более изящный и остроумный, чем первый.
Ученое собрание согласно закивало головами, присоединяясь таким образом к мнению своего повелителя. Но Мате показалось, что магистр Иоанн чем-то озабочен. Его и без того беспокойные глазки зыркали по сторонам с каким-то особенно тревожным и загнанным выражением. Похоже, успех Леонардо его не очень-то обрадовал…
— Не будем, однако, забывать, — продолжал Фридрих, — что перед нами не только замечательный вычислитель, но и тонкий геометр, человек, написавший «Практику геометрии» — книгу, которая пополняет наши геометрические познания, почерпнутые у древних, оригинальными доказательствами и изысканиями, принадлежащими самому мессеру Леонардо… Помнится, это сочинение посвящено вам, магистр Доменик?
Тот поклонился.
— Так кто же пожелает задать мессеру Леонардо вопрос из геометрии? — спросил император, обводя глазами свое ученое воинство. — Вы, магистр Теодор? Прошу!
«Наконец-то!» — подумал Фило, которому давно не терпелось услыхать этого длиннокудрого итальянца, обладавшего удивительно нежным и поэтичным лицом.
Его постигло разочарование. Голос Теодора, высокий, скрипучий, оказался далеко не таким привлекательным, как его внешность. И вот этим-то скрипучим голосом изложил он свое задание: Леонардо должен вписать в квадрат равносторонний пятиугольник так, чтобы одним из его углов служил угол заданного квадрата.
…Услыхав эту задачу, Мате прямо затрясся от любопытства. Но…
Но тут вступил в свои права закон неожиданныхпомех. Вряд ли существует на земле человек, который не испытал на себе его действия.
Допустим, вы сидите у телевизора и с наслаждением следите за событиями умопомрачительного детективного фильма. Трах! На самом интересном месте гаснет свет. Или же в кармане у вас лежат билеты на новый спектакль. Для того чтобы добыть их, вы встали в шесть часов утра и выстояли длиннющую очередь. Но накануне долгожданного дня выясняется, что вы заболели свинкой.
Фило и Мате свинкой не заболели, зато судьба подложила им откормленную свинью. Когда Леонардо взял мелок, собираясь приступить к решению, все находящиеся в кабинете, в том числе Фридрих, сгрудились над столом и совершенно заслонили и чертеж, и самого Фибоначчи, объяснения которого звучали так глухо, что разобрать их было немыслимо. Когда же склоненные над столом головы вновь поднялись, на черной полированной поверхности оказался не один, а целых три чертежа.
— Что это? — удивился Фило. — Кажется, он походя решил еще две задачи!
— Но каким способом? — чуть не плакал Мате. — Теперь нам этого никогда не узнать!
— Полно вам хлюпать, — пристыдил его Фило. — Узнаете у него самого.
Слова его несколько успокоили Мате, и приятели снова прильнули к прорезям в занавесках.
Они сделали это как раз вовремя для того, чтобы услышать похвалы, которые Фридрих расточал Фибоначчи. Император не скупился на слова: он в восторге! Ход рассуждений мессера Леонардо совершенно необычен и свидетельствует не только о глубокой осведомленности, но прежде всего о блестящем и оригинальном дарований…
Леонардо слушал рассеянно. Не то чтобы ему были неприятны монарший любезности — напротив! Но непривычное внимание к его скромной особе утомило его. Он оживился только тогда, когда Фридрих пожелал получить от него письменный разбор его решений. Это дело другое! Тут уж речь не о нем самом, а о математике! И, прижав руку к сердцу, Фибоначчи заверил его величество, что представит ему подробное изложение в самое ближайшее время.
«Вот оно! — подумал Мате. — Сейчас Фридрих заговорит о Неаполе».
Но тут с места поднялся магистр Иоанн, и Мате понял, что испытание еще не окончено.
Задание Иоанна было немногословным, но зато куда труднее предыдущих: если к третьей степени некоего числа прибавить его удвоенный квадрат и, сверх того, то же число, увеличенное в десять раз, то сумма будет равна двадцати. Чему равно это число?
Мате забеспокоился: ведь это задача на кубическое уравнение! Но Леонардо и не думал волноваться. Он неторопливо вычертил прямоугольник, обозначив высоту его числом 10, затем пристроил по обе стороны этого прямоугольника два других с теми же высотами и стал рассуждать.
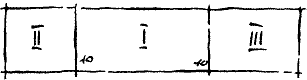
Допустим, сказал он, что основание первого прямоугольника равно искомому числу, основание второго — одной пятой квадрата этого числа, а основание третьего — одной десятой куба того же числа. Из этого следует, что общая площадь всех трех прямоугольников должна быть равна 20. Следовательно, сумма их оснований равна 2, ибо площадь прямоугольника равна произведению высоты на основание. Но раз так, стало быть, искомое число меньше двух, и если принять, что оно целое, то оно может быть равно только единице. Однако, подставив единицу в условие нашей задачи, мы получим не 20, а всего лишь 13. Значит, искомое число больше единицы и находится где-то между единицей и двойкой…
— Готов поклясться решетом Эратосфена, что дробь у него получится иррациональная, — нервничал Мате. — Но как он ее вычислит?
— Чем понапрасну дергаться и теряться в догадках, вы бы слушали да записывали, — сердито посоветовал Фило.
Лучше бы ему помолчать! Мате полез за блокнотом, но пуговица на рукаве его рубашки зацепилась за бахрому занавески, и, опуская руку в карман, он с силой дернул на себя бархатное полотнище, исторгнув из него целое облако пыли.
После этого, сами понимаете, филоматикам было уже не до записей. Все их усилия были направлены на то, чтобы протереть глаза и не раскашляться.
Кое-как справившись с этим, они вновь попытались заглянуть в зал, но тут выяснилось, что прорези в портьерах куда-то запропастились. Фило и Мате принялись искать их, судорожно перебирая тяжелые складки. Толстая малиновая ткань заходила волнами. Когда же прорези наконец обнаружились, Леонардо уже записывал ответ: 10 22I 7II 42III 33IV 4V 40VI.
У Фило глаза на лоб полезли: что за странная запись! Мате собирался ему ответить, но перед ними снова вырос восточный истукан. Все это время он дежурил в кабинете за колонной. Портьерная буря не ускользнула от его внимательного взора, и мгновение спустя приятели очутились за пределами балкона, а там и за пределами дворца.
НА ДВОРЦОВОЙ ЗАВАЛИНКЕ
— Что будем делать? — спросил Фило, мрачно поглядывая на запретное для них теперь императорское палаццо.
— Ждать! — отрезал Мате.
Зная, в какую сторону пойдет Фибоначчи, возвращаясь домой, изгнанники свернули за угол и присели в тени колоннады на каменный выступ дворцового фундамента. На соседних улицах шумел карнавал, но здесь по какой-то странной случайности было безлюдно. К тому же отсюда можно было обозревать нужную часть площади, не привлекая внимания часовых.
Перебирая в памяти только что виденное, Мате с невольной симпатией отметил про себя веселую доброжелательность Фридриха, его простое, уважительное обхождение с Фибоначчи.
— А знаете, — сказал он, — император, конечно, тиран и все такое прочее, но, по-моему, сегодня он вел себя на пять с плюсом.
— Да, не то что его капельдинер! — поддакнул Фило.
— Вы хотели сказать — камердинер?
— Нет, нет, именно капельдинер. Ведь он выставил нас из театральной ложи!
— Вот вы о чем! — понял наконец Мате. — Этот балкон и впрямь напоминает ложу.
— Потерять такие места! — горевал Фило.
— Что — места! Упустить объяснения Фибоначчи!
— Слушайте, Мате, — взвыл Фило, — мы же, кажется, договорились, что вы спросите о пропущенном у самого Леонардо. Хотя, по правде говоря, не понимаю, о чем тут спрашивать. Насколько я помню, задача сводится к кубическому уравнению. Так решите его сами, и дело с концом!
— Вы забываете, что я буду его решать так, как принято в двадцатом столетии. Но как это делали в тринадцатом?
— Во всяком случае, очень сложно! — убежденно изрек Фило. — Помните, какой там стоял загадочный ответ?
Мате улыбнулся. Вот уж загадка, которую разгадать нетрудно! Попросту Фибоначчи записал результат в шестидесятеричной системе счисления.
— Как же так? — удивился Фило. — Сам же ввел десятичную, а считает в шестидесятеричной…
— Вы думаете, десятичная система вошла в обиход сразу? Сомневаюсь. В Европе тринадцатого века ею наверняка пользовались очень немногие. Как видите, даже сам мессер Леонардо не прочь иногда вернуться к старому, привычному счету.
Испугавшись, как бы ему не вздумали читать лекцию о шестидесятеричной системе, Фило решил выбрать из двух зол меньшее и срочно вспомнил о шуточной задачке, с которой Мате собирался познакомить Фибоначчи перед приходом магистра Доменика.
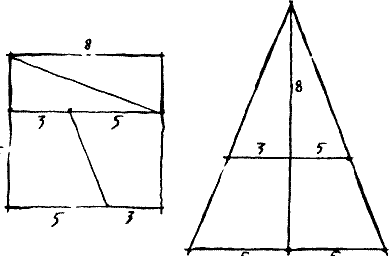
Мате беспрекословно вытащил многострадальный блокнот и начертил квадрат, состоящий из 64 клеток.
— Сторона этого квадрата равна 8, — объяснил он. — Заметьте, что это одно из чисел Фибоначчи. Разделим квадрат на два прямоугольника со сторонами, также равными двум соседним числам Фибоначчи. В данном случае это 3 и 5. В меньшем прямоугольнике проведем диагональ — она разобьет его на два одинаковых треугольника с основаниями 3 и высотами 8. Большой прямоугольник разобьем на две одинаковые трапеции, у которых высоты равны 5, а основания — 3 и 5. Теперь составим из этих четырех частей один большой треугольник с основанием 10 и высотой 13 и вычислим его площадь по обычной формуле. Что у нас получится?
— Если не ошибаюсь, 65, — неуверенно промямлил Фило. — А дальше что?
— Куда уж дальше! Разве вы не видите, что площадь этого треугольника на единицу больше площади заданного квадрата?
Фило растерянно посмотрел на чертеж: откуда же взялась лишняя единица?
— А уж это соблаговолите определить сами! Но будьте уверены: если сторона квадрата есть сумма двух соседних чисел Фибоначчи, то, поступив указанным образом, вы непременно увидите, что площадь треугольника либо больше, либо меньше площади квадрата ровно на единицу.
Фило надулся, сразу став похожим на рассерженного воробья.
— Всегда вы так! Заинтригуете и оставите барахтаться одного. Как щенка в воде.
— Ничего, выплывете, — обнадежил его Мате.
— Разве что с помощью ложного предположения, — угрюмо пошутил Фило.
— Уж не кажется ли вам, что метод ложного предположения позволяет предполагать любую произвольную чепуху?
— Но разве Леонардо выбрал не первые попавшиеся числа?
— Конечно, нет! Как вы помните, в задаче магистра Доменика было два требования. Одно состояло в том, что каждое из четырех чисел, начиная со второго, должно быть больше предыдущего в два раза; другое — в том, что сумма этих чисел должна быть равна десяти. Фибоначчи начал с того, что выполнил первое требование, не принимая пока во внимание второго.
— Попросту говоря, схитрил.
— И хорошо сделал, — уважительно сказал Мате. — Без такой хитрости в науке не обойтись. Настоящий ученый никогда не изучает всех сторон явления сразу. Да это и невозможно! Возьмем, например, такую науку, как сопротивление материалов…
— А, это ту, которой занимался Галилей! — вспомнил Фило. — О ней мне известно только то, что ее сокращенно называют сопроматом и что редко кто из студентов умудряется сдать экзамен по сопромату с первого раза.
— Не слишком много, зато верно, — согласился Мате. — Так вот, у каждого материала целая куча свойств: твердость, упругость, пластичность, вязкость, текучесть и так далее. Изучая его сопротивляемость внешним нагрузкам, учесть все эти качества в один присест немыслимо. Вот почему ученые начинают с того, что рассматривают тело как абсолютно твердое, отвлекаясь от всех его прочих свойств. Изучив воздействие внешних сил на поведение абсолютно твердого тела, они переходят к исследованию следующего свойства: идеальной упругости. Потом сюда подключается идеальная пластичность… Так постепенно из всех этих отвлеченностей складывается наука о сопротивлении конкретных материалов.
— Вы хотите сказать, что вместо реальных явлений наука рассматривает какую-то абстракцию? Иными словами, то, чего на самом деле нет?
— Вы меня не поняли, — раздраженно возразил Мате. — Я хочу сказать, что, не умея отвлеченно мыслить, нельзя по-настоящему изучить реальный мир. А что, как не математика, воспитывает в нас такое умение? Вот почему эта наука так важна для каждого человека, независимо от того, к какой профессии он себя готовит.
В эту минуту мимо проходила старая женщина, ведя под уздцы понурого осла с двумя перекинутыми через спину мешками. Как тут было не вспомнить задачи о семи старухах!
Фило признался, что не очень-то понял, как мессер Леонардо умудрился получить один и тот же результат совершенно разными способами. Но Мате не находил в этом ничего непонятного. Ведь второй способ вытекает из первого!
— К чему, собственно, сводится задача? — сказал он. — Она сводится к вычислению и суммированию последовательных степеней числа 7. Напишем этот ряд: 70 + 71 + 72 + 73 + 74 + … Сложим первые два члена: 70 + 71 = 1 + 7 = 8. Теперь суммируем первые три члена: 70 + 71 + 72 = 1 + 7(1 + 71) = 1 + 7 х 8 = 57. Продвигаясь дальше, получим: 70 + 71 + 72 + 73 = 1 + 7(1 + 71 + 72) = 1 + 7 x 57 = 400. А теперь вглядитесь внимательно в мою запись, и вы увидите, что левые части равенства представляют собой то, из чего исходил Леонардо в первом способе решения, а правые — то, что он получил вторым…
Мате не договорил, чем-то пораженный. Наконец-то! Наконец он вспомнил, где видел задачу, похожую на эту. У Ахмеса!
— Это кто же? Ваш родственник? — подтрунил Фило.