· Среднее арифметическое – Х (среднее значение результатов, показанных учащимися)
· Среднее квадратическое отклонение – s (мера рассеяния результатов, показанных учащимися от более низких к более высоким, при этом самые низкие и самые высокие математически отбрасываются)
Примечание. Значение среднего арифметического не даёт полной информации о варьирующем признаке. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки и записываются в виде Х + s.
· Ошибка среднего арифметического – m (отклонение оценок генеральных параметров, в частности среднего арифметического, от истинных значений этих параметров называются статистическими ошибками. В качестве оценки стандартного отклонения выборочного среднего используется величина, называемая ошибкой среднего арифметического, которая показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего арифметического его выборочную оценку. Поэтому вычисление среднего арифметического часто указывается в виде Х±х для более точной оценки среднего арифметического)
· Число степеней свободы для двух наборов - v
· t - критерий Стьюдента
- На основании t-критерия и v определяли степень достоверности Р (уровень значимости) полученных результатов используя таблицу.
Примечание. Р – экспериментальный уровень значимости. Точное значение обычно не указывают, а окончательные результаты приводят в следующем виде: 1) если вычисленное значение t не превосходит критического значения на уровне значимости α=0,05, то различие считается статистически не значимым; 2) если вычисленное по выборке значение критерия превышает критические значения при α=0,05 (5%), α=0,01 (1%) или α=0,001 (0,1%), то записывают Р<0,05, Р<0,01 или Р<0,005. Это означает, что наблюдаемые различия статистически значимы на уровне значимости 0,05 (5%), 0,01(1%) или 0,001 (0,1%).
Вначале вычислите величину среднего арифметического Х по следующей формуле: Х = 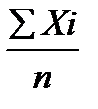 , где
, где 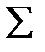 - символ суммы, Хi – значение отдельного измерения (варианта), n – общее число вариантов.
- символ суммы, Хi – значение отдельного измерения (варианта), n – общее число вариантов.
Далее определите величину 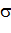 - среднее квадратическое отклонение по формуле:
- среднее квадратическое отклонение по формуле: 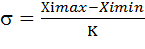 , где Ximax - наибольший показатель; Ximin - наименьший показатель; К -табличный коэффициент. Значение коэффициента К соответствует числу измерений в группе. Например, если в группе 10 человек, то К=3,08., если в группе 15 человек, то К=3,47; если в группе 36 человек, то К=4,24.
, где Ximax - наибольший показатель; Ximin - наименьший показатель; К -табличный коэффициент. Значение коэффициента К соответствует числу измерений в группе. Например, если в группе 10 человек, то К=3,08., если в группе 15 человек, то К=3,47; если в группе 36 человек, то К=4,24.
Таблица 30 - Значение коэффициента К
| n | ||||||||||
| - | - | 1,13 | 1,69 | 2,06 | 2,33 | 2,53 | 2,70 | 2,85 | 2,97 | |
| 3,08 | 3,17 | 3,26 | 3,34 | 3,41 | 3,47 | 3,53 | 3,59 | 3,64 | 3,69 | |
| 3,74 | 3,78 | 3,82 | 3,86 | 3,90 | 3,93 | 3,96 | 4,00 | 4,03 | 4,06 | |
| 4,09 | 4,11 | 4,14 | 4,16 | 4,19 | 4,21 | 4,24 | 4,26 | 4,28 | 4,30 | |
| 4,32 | 4,34 | 4,36 | 4,38 | 4,40 | 4,42 | 4,43 | 4,45 | 4,47 | 4,48 | |
| 4,50 | 4,51 | 4,53 | 4,54 | 4,56 | 4,57 | 4,59 | 4,60 | 4,61 | 4,63 | |
| 4,64 | 4,65 | 4,66 | 4,68 | 4,69 | 4,70 | 4,71 | 4,72 | 4,73 | 4,74 | |
| 4,76 | 4,76 | 4,78 | 4,79 | 4,80 | 4,81 | 4,82 | 4,82 | 4,84 | 4,84 | |
| 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,92 | 4,92 | 4,93 | |
| 4,94 | 4,95 | 4,96 | 4,96 | 4,97 | 4,98 | 4,99 | 4,99 | 5,00 | 5,01 | |
| 5,02 | 5,02 | 5,03 | 5,04 | 5,04 | 5,05 | 5,06 | 5,06 | 5,07 | 5,08 | |
| 5,08 | 5,09 | 5,10 | 5,10 | 5,11 | 5,11 | 5,12 | 5,13 | 5,13 | 5,14 |
Находили ошибку среднего арифметического - х по формуле: 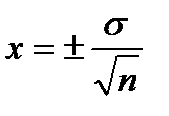 .
.
Параметрический t-критерий Стьюдента находили по формуле: 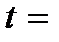
Следует учитывать, что число вариантов, и дисперсия в двух группах может быть, как одинаково, так и нет, а для определения достоверности различия - это необходимо учитывать. Учитывая данный факт, прежде чем оценить значение t-критерия Стьюдента, следует найти число степеней свободы v по следующим формулам:
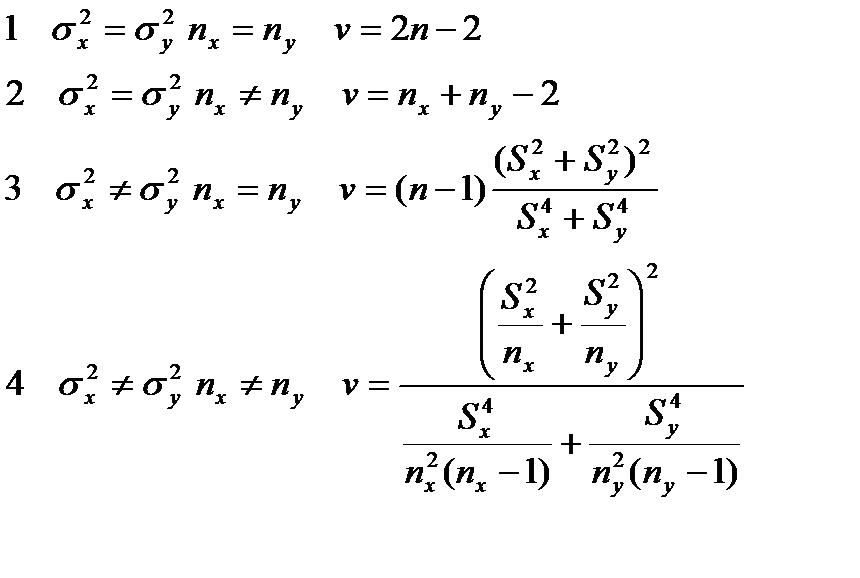
Далее полученное значение оценивается по таблице «t – распределение Стьюдента для оценки статической достоверности различий в группах”.
Таблица 30 - Критические значения двустороннего t – критерия Стьюдента (v – число степеней свободы)
| Уровни значимости | |||||||||
| v | 0,1 | 0,05 | 0,01 | 0,001 | v | 0,1 | 0,05 | 0,01 | 0,001 |
| 6,314 | 12,706 | 63,657 | 636,619 | 1,721 | 2,080 | 2,831 | 3,819 | ||
| 2,92 | 4,308 | 9,925 | 31,599 | 1,717 | 2,074 | 2,819 | 3,792 | ||
| 2,353 | 3,182 | 5,841 | 12,924 | 1,714 | 2,069 | 2,807 | 3,768 | ||
| 2,132 | 2,776 | 4,604 | 8,610 | 1,711 | 2,064 | 2,797 | 3,745 | ||
| 2,015 | 2,571 | 4,032 | 6,869 | 1,708 | 2,060 | 2,787 | 3,725 | ||
| 1,943 | 2,447 | 3,707 | 5,959 | 1,706 | 2,056 | 2,779 | 3,707 | ||
| 1,859 | 2,365 | 3,499 | 5,408 | 1,703 | 2,052 | 2,771 | 3,690 | ||
| 1,860 | 2,306 | 3,355 | 5,041 | 1,701 | 2,048 | 2,763 | 3,674 | ||
| 1,833 | 2,262 | 3,250 | 4,781 | 1,699 | 2,045 | 2,756 | 3,659 | ||
| 1,812 | 2,228 | 3,169 | 4,587 | 1,697 | 2,042 | 2,750 | 3,646 | ||
| 1,796 | 2,201 | 3,106 | 4,437 | 1,684 | 2,021 | 2,704 | 3,551 | ||
| 1,782 | 2,179 | 3,055 | 4,318 | 1,676 | 2,009 | 2,678 | 3,505 | ||
| 1,771 | 2,160 | 3,012 | 4,221 | 1,664 | 2,000 | 2,660 | 3,505 | ||
| 1,761 | 2,145 | 2,977 | 4,140 | 1,664 | 1,990 | 2,639 | 3,416 | ||
| 1,753 | 2,131 | 2,947 | 4,073 | 1,660 | 1,984 | 2,626 | 3,391 | ||
| 1,746 | 2,120 | 2,921 | 4,015 | 1,658 | 1,980 | 2,617 | 3,373 | ||
| 1,170 | 2,110 | 2,898 | 3,965 | 1,653 | 1,972 | 2,601 | 3,340 | ||
| 1,734 | 2,101 | 2,878 | 3,922 | 1,648 | 1,965 | 2,586 | 3,310 | ||
| 1,729 | 2,093 | 2,861 | 3,883 | ∞ | 1,645 | 1,960 | 2,580 | 3,291 | |
| 1,725 | 2,086 | 2,845 | 3,850 | ||||||
| 0,9 | 0,95 | 0,99 | 0,999 | 0,9 | 0,95 | 0,99 | 0,999 | ||
| Доверительные уровни |
Примечание. Таблица составлена по Л.Н. Большеву и Н.В. Смирнову,1968; М.Дж. Кендаллу и А.М. Стьюарту,1973.