Если признаки, свойства, параметры и т. П. не поддаются количественному измерению и не распределяются в вариационный ряд, т. Е. тогда, когда мы пользуемся шкалой наименований, корреляция между ними устанавливается по наличию этих признаков. Если анализируется связь только между двумя качественными признаками, прибегают к вычислению коэффициента ассоциации (rа). При этом данные о наличии или отсутствии каждого признака группируются в четырехпольную корреляционную таблицу:
| есть | нет | ||
| 1-й признак | а | b | a+b = n1 |
| 2-й признак | с | d | c+d = пг |
| а+с | b+d | N = n1+n2 |
Коэффициент ассоциации вычисляется по следующей формуле:
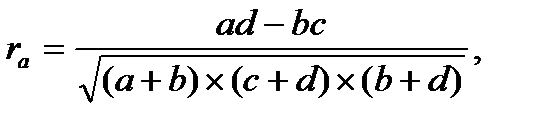
где а, b, с, d – численности альтернативных признаков, расположенные в клетках корреляционной таблицы. Одним из условий правильного применения коэффициента ассоциации является требование, согласно которому ни одна из частот четырехпольной таблицы не должна быть меньше 5. Для того чтобы легче было понять методику расчета коэффициента ассоциации, обратимся к примеру.
Допустим, необходимо изучить связь между чрезмерно строгой дисциплиной в семье и проявлением упрямства и непослушания у занимающихся в отделении ДЮСШ. Результаты наблюдений внесем в четырехпольную корреляционную таблицу:
| есть | нет | ||
| 1. Упрямство | а = 7 | b = 8 | а+b=15 |
| 2. Строгая дисциплина | с -5 | d = 10 | с+d = 15 |
| а+с=12 | b+d=18 | N=30 |
Подставим эти значения в формулу и рассчитаем коэффициент ассоциации:
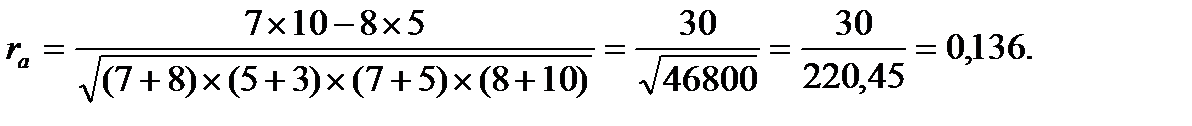
Значение полученного коэффициента показывает, что между строгой дисциплиной в семье и проявлением у занимающихся упрямства и непослушания обнаруживается слабая положительная связь. Однако прежде чем делать окончательные выводы, необходимо проверить, не является ли эта величина случайной. Проверка достоверности в данном случае осуществляется следующим образом. Если величина 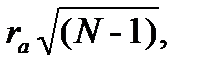 превосходит указанное в таблице критическое значение для принятого уровня значимости и числа степеней свободы (К=N - 2),то наличие связи считается достоверным, и наоборот. В нашем примере
превосходит указанное в таблице критическое значение для принятого уровня значимости и числа степеней свободы (К=N - 2),то наличие связи считается достоверным, и наоборот. В нашем примере 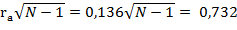 .
.
Теперь по таблице 32найдем значение коэффициента корреляции при Р = 0,05 и числе степеней свободы К = N-2 = 30 - 2 = 28.Это значение равно 0,36.Вычислим величину 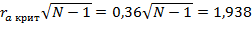 .Произведенный расчет показывает,
.Произведенный расчет показывает, 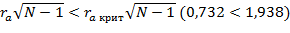 .
.
Следовательно, обнаруженная положительная связь между чрезмерно строгой дисциплиной в семье и проявлениями упрямства и непослушания у детей считается недостоверной (rа= 0,136 при Р > 0,05). Очевидно, при увеличении числа наблюдений наличие такой связи может оказаться достоверным.
Таблица 32 - Значения коэффициента корреляции при 5% -ном уровне значимости и числе степеней свободы K=N-2
| число степеней свободы | коэффициент корреляции | число степеней свободы | коэффициент корреляции |
| 0.75 | 0.37 | ||
| 0.71 | 0.36 | ||
| 0,67 | 0,36 | ||
| 0,63 | 0,35 | ||
| 0.60 | 0.33 | ||
| 0,58 | 0,30 | ||
| 0.55 | 0.29 | ||
| 0.53 | 0,27 | ||
| 0,51 | 0,25 | ||
| 0,50 | 0,23 | ||
| 0,48 | 0,22 | ||
| 0.47 | 0,21 | ||
| 0.46 | 0,20 | ||
| 0.44 | 0.17 | ||
| 0.43 | 0.16 | ||
| 0.42 | 0.14 | ||
| 0.41 | 0.11 | ||
| 0.40 | 0.10 | ||
| 0.40 | 0,09 | ||
| 0,39 | 0,07 | ||
| 0,38 | 0,06 | ||
| 0,39 | 0.06 |