Наиболее известным показателем связи является ранговый коэффициент корреляции Спирмена, определяемый по следующей формуле:
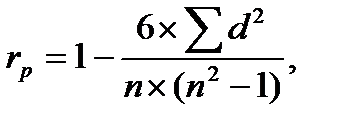
где Σ- знак суммирования; d - разность между рангами рассматриваемых признаков; п - общее число наблюдений (парных).
Чтобы выяснить, существует ли связь между двумя признаками (свойствами), нужно ранжировать их значения и посмотреть, как они располагаются по отношению друг к другу. Если возрастающим значениям одного признака соответствуют однохарактерные значения другого признака, то между ними налицо положительная связь. Если же при возрастании одного признака значения другого последовательно убывают, то это свидетельствует о наличии отрицательной связи между ними. При ранговой корреляции сравнивают не сами значения измерений или числа измерений, а только порядок (ранги), поэтому вычисление рангового коэффициента возможно только тогда, когда результаты измерений получены на основе шкалы не ниже порядковой (например, баллы или другие условные единицы измерения). Ранговый коэффициент не рекомендуется применять, если связанных пар меньше 5 и больше 20.
Технику вычисления рангового коэффициента легко усвоить на конкретном примере. Допустим, что из двух рядов измерений мы получили следующие значения:
| Испытуемые | 4 | |||||||||
| Признак А | ||||||||||
| Признак Б |
Для того чтобы вычислить ранговый коэффициент по приведенной выше формуле, необходимо произвести предварительные расчеты (табл. 33).
Таблица 33.
| Испытуемые | Ряды измерений | Ранговые числа | Разность | ||||
| А | Б | А1 | Б1 | d = А1-Б1 | d2 | ||
| А | |||||||
| Б | -3 | ||||||
| Ж | |||||||
| В | -2 | ||||||
| 3,5 | 1,5 | 2,25 | |||||
| Д | -2 | ||||||
| И | -2 | ||||||
| К | 3,5 | 4,5 | 20,25 | ||||
| Е | |||||||
| Г |
п = 10 Σ d2i =48,50
Для вычисления необходимых данных следует:
1. Произвести ранжирование показателей признака А в убывающем (возрастающем) порядке и расставить испытуемых в порядке убывания (возрастания) этого признака - 1-я, 2-я колонки таблицы.
2. Рядом со значениями признака А для каждого испытуемого проставить значения показателей признака Б - 3-я колонка таблицы.
3. По каждому признаку проставить ранговые числа. При одинаковых значениях (например, 110 и 110 по признаку Б) общим для них будет среднеарифметический ранг 3,5 - 4-я и 5-я колонки таблицы.
4. Вычислить разность рангов (d = A1-Б1) с сохранением соответствующего знака - 6-я колонка.
5. Возвести разность рангов в квадрат (d2) - 7-я колонка.
6. Вычислить сумму квадратов разности рангов (Σd2i).
7. Полученные таким образом значения подставить в известную формулу и вычислить коэффициент ранговой корреляции:
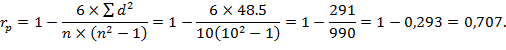
Вычисленное значение коэффициентов ранговой корреляции в данном случае свидетельствует о наличии между признаками А и Б сильной положительной связи. Однако необходимо проверить, насколько достоверно значение рассчитанного нами коэффициента корреляции. Для этого сравним его с критическим значением. Если вычисленный коэффициент ранговой корреляции превышает значение критического (rр фак > rр крит), то наличие связи считается достоверным, и наоборот. По таблице 34, в которой приведены критические значения rр для различных чисел парных наблюдений (п) и двух уровней значимости (Р = 0,05 и Р — 0,01), находим критическое значение для п = 10. Оно равно 0,564 при уровне значимости 0,05 и 0,746 при уровне значимости 0,01. Следовательно, вычисленный нами коэффициент превышает критическое значение при уровне значимости 0,05 (0,707 > 0,564) и проявление связи между признаками А и Б можно считать достоверным (rр= 0,707 при Р < 0,05).
Таблица 34 - Критические значения коэффициента корреляции.
| Число коррелируемых пар п | Р=0,05 | р=0.01 1 | Число коррелируемых пар n | р=0.05 | р=0,01 |
| 1.000 | — | 0,456 | 0.645 | ||
| 0,900 | 1.000 | 0.425 | 0.601 | ||
| 0.829 | 0,943 | 0.399 | 0.564 | ||
| 0,714 | 0,893 | 0.377 | 0.534 | ||
| 0.643 | 0.833 | 0,359 | 0,508 | ||
| 0,600 | 0.783 | 0,343 | 0,485 | ||
| 0,564 | 0.746 | 0.329 | 0.465 | ||
| 0,506 | 0.712 | 0.317 | 0.448 | ||
| 0,306 | 0.432 |