Пример 1.
Найдите все значения 
, при каждом из которых уравнение
имеет ровно три различных корня.
Ответ: 
; 
; 
.
Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта: 4 балла.
Пример 2.
Найдите все значения , при каждом из которых уравнение
имеет ровно три различных корня.
Ответ: ; ; .
Комментарий.
Решение логично, все шаги присутствуют, но при решении неравенства в пункте 2) допущена ошибка вычислительного характера, что соответствует критерию на 2 балла.
Оценка эксперта: 2 балла.
Пример 3.
Найдите все значения , при каждом из которых уравнение
имеет ровно три различных корня.
Ответ: ; ; .
Комментарий.
Получены корни уравнения 
, 
, 
и задача сведена к исследованию полученных корней при условии 
(есть только указание).
Оценка эксперта: 1 балл.
Пример 4.
Найдите все значения , при каждом из которых уравнение
имеет ровно три различных корня.
Ответ: 
; 
; .
Комментарий.
В решении присутствуют все этапы. Решение соответствует критерию на 3 балла: с помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек 
и/или 
.
Оценка эксперта: 3 балла.
Пример 5.
Найдите все значения , при каждом из которых система уравнений
имеет ровно два решения.
Ответ: 
.
Комментарий.
Ход решения ясен, изложен более чем подробно. Ошибок нет, кроме недочета: концы промежутка не включены в ответ.
Оценка эксперта: 3 балла.
Пример 6.
Найдите все значения 
, при каждом из которых система уравнений
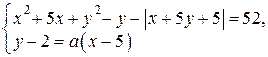
имеет ровно два решения.
Ответ: 
.
Комментарий.
Решение и ответ верные, хотя нет обоснования, почему для касания « должно быть равно –8» или «…7/4».
Оценка эксперта: 4 балла.
Критерии проверки и оценка решений заданий 19 ЕГЭ-2018
Содержательно задание №19 проверяет в первую очередь не уровень математической (школьной) образованности, а уровень математической культуры. Формирования культуры происходит на протяжении всех лет обучения (и не только в школе). Для решения этой задачи никаких фактов из теории чисел типа теоремы Вильсона, чисел Мерсенна, малой теоремы Ферма, теории сравнений и т.п. для решения этих заданий не требуется. Тот, кто эти факты знает, разумеется, может их использовать, но, подчёркиваем, при решении всегда можно обойтись и без них.
Условия задания №19 разбиты на пункты. По существу, задача разбита на ряд подзадач (частных случаев), последовательно решая которые можно в итоге справится с ситуацией в целом.
Задача 19 (демонстрационный вариант 2018 г).
Задача 1.
В последовательности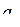 
, 
, …, 
, 
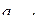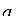, состоящей из целых чисел,
, 
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Решение.
а) Например, последовательность 1, 2, 3, 0, 5, 
, 7, 
, …, 233, 
, 235
удовлетворяет условию задачи (чередуются суммы чисел 3 и 5).
б) Поскольку 3, 5 и 25 — нечётные числа, любые два соседних члена последовательности имеют разную чётность. На нечётных местах должны стоять нечётные числа, а на чётных — чётные. Число 235 нечётное, поэтому оно не может стоять на чётном месте. Значит, последовательность не может состоять из 1000 членов.
в) Рассмотрим три члена последовательности: 
, 
, 
.
Поскольку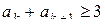 
, 
, получаем: 
.
В предыдущем пункте было показано, что последовательность должна состоять из нечётного числа членов. Пусть 
, тогда
; 
,
откуда 
. Значит, последовательность состоит не менее чем из 23 чисел.
Приведём пример последовательности, удовлетворяющей условию задачи, состоящей из 23 членов: 1, 2, 23, 
, 45, 
, 67, 
, 89, 
, 111, 
, 
, 
, 155, 
, 175, 
, 195, 
, 215, 
, 235.
Ответ: а) например, 1, 2, 3, 0, 5, , 7, , …, 233, , 235; б) нет; в) 23.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: — пример в п. а; — обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 2.
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Решение.
а) Если на доске записано 29 зелёных чисел: 3, 6, …, 87 — и одно красное
число 21, то их сумма меньше 1395.
б) Пусть на доске ровно одно красное число. Тогда зелёных чисел 29,
а их сумма не меньше, чем сумма 29 наименьших чисел, делящихся на 3:
.
Это противоречит тому, что сумма написанных чисел равна 1067.
в) Пусть на доске написано 
красных чисел и 
зелёных чисел. Тогда сумма красных чисел не меньше 
,
а сумма зелёных чисел не меньше
.
Таким образом, 
; 
,
откуда, учитывая, что — целое, получаем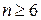 
.
Приведём пример 6 красных чисел и 24 зелёных чисел, сумма которых
равна 1067: 7, 14, 21, 28, 35, 56, 3, 6, …, 66, 69, 78.
Ответ: а) да; б) нет; в) 6.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: — обоснованное решение пункта а; — обоснованное решение пункта б; — искомая оценка в пункте в; — пример в пункте в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |