Задание №15 – это неравенство – дробно-рациональное, логарифмическое или показательное.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением / включением граничных точек ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « » вместо «
» вместо «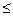 », или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».
», или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».
Задача 15 (демонстрационный вариант 2018 г).
Решите неравенство  .
.
Решение.
Пусть 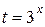 , тогда неравенство примет вид:
, тогда неравенство примет вид:
 ;
;  ;
;
 ;
;  ,
,
откуда  ;
;  .
.
При 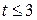 получим:
получим:  , откуда
, откуда 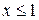 .
.
При  получим:
получим: 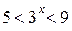 , откуда
, откуда 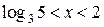 .
.
Решение исходного неравенства:
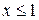 ;
; 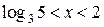 .
.
Ответ:  ;
; 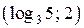 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением точки 1, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 1.
Решите неравенство  .
.
Решение.
Пусть 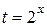 , тогда неравенство примет вид:
, тогда неравенство примет вид:
 ;
;  ;
;
 , где
, где 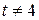 ;
;  , где
, где  ,
,
откуда 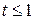 ;
;  ;
;  .
.
При  получим:
получим:  , откуда
, откуда 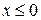 .
.
При  получим:
получим: 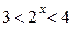 , откуда
, откуда  .
.
При  получим:
получим: 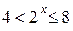 , откуда
, откуда  .
.
Решение исходного неравенства:
 ;
; 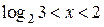 ;
;  .
.
Ответ: 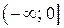 ;
; 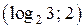 ;
; 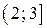 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением точек 0 и/или 3, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задача 2.
Решите неравенство 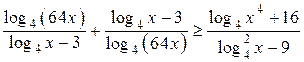 .
.
Решение.
Пусть  , тогда неравенство примет вид:
, тогда неравенство примет вид:
 ;
;  ;
;
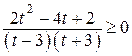 ;
;  ,
,
откуда  ;
; 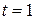 ;
;  .
.
При  получим:
получим:  , откуда
, откуда 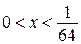 .
.
При 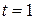 получим:
получим:  , откуда
, откуда  .
.
При  получим:
получим:  , откуда
, откуда  .
.
Решение исходного неравенства: 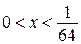 ;
; 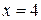 ;
;  .
.
Ответ: 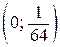 ; 4;
; 4;  .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением точки 4, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Примеры оценивания решений задания 15
Пример 1.
Решите неравенство  .
.
Ответ: 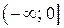 ;
;  ;
; 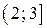 .
.

Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта: 2 балла.
Пример 2.
Решите неравенство 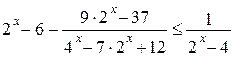 .
.
Ответ: 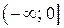 ;
;  ;
; 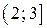 .
.

Комментарий.
В решение содержится запись «ОДЗ», которая может трактоваться по-разному.
Ответ получен неверный, но он отличается от верного только исключением точки 3.
Оценка эксперта: 1 балл.
Пример 3.
Решите неравенство  .
.
Ответ: 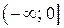 ;
;  ;
;  .
.
 .
.
Комментарий.
При решении неравенства допущена ошибка – допущен неравносильный переход. Это привело к неверному ответу.
Оценка эксперта. 0 баллов.
Пример 4.
Решите неравенство 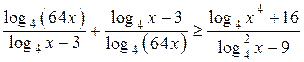 .
.
Ответ:  ; 4;
; 4;  .
.

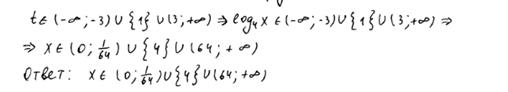
Комментарий.
Обоснованно получен верный ответ.