Все величины делятся на абсолютные, относительные, средние. Абсолютные величины характеризуют явление, несут информацию о размере явления. Для анализа употребляются редко:
1.При особой значимости (случаи чумы)
2.Если величины длительное время не меняются (любые нормы, нормативы)
3.Для характеристики размаха или размера явления (кол-во лейкоцитов в поле зрения)
4.Если при перерасчете из абсолютных величин в относительную получаются очень малые значения, то данные сообщаются в абсолютных величинах.
Статистический показатель - одна из многих количественных характеристик статистической совокупности, численное выражение внутренней сущности изучаемого явления.
Показатели, в зависимости от охвата единиц совокупности, подразделяются на индивидуальные, характеризующие отдельный объект, и сводные, характеризующие группу объектов. Также статистические показатели можно классифицировать следующим образом:
- абсолютные;
- относительные;
- средние.
Кроме того, для комплексной оценки здоровья населения, медицинской и экономической деятельности учреждений здравоохранения на основе математических моделей разрабатываются интегральные статистические показатели.
Абсолютные статистические показатели имеют определенные размерность и единицы измерения, показывают количество, численность чего-то или кого-то, например численность населения, количество больничных коек, врачей, родившихся, умерших людей и др.
Относительные статистические показатели более объективно выражают количественные соотношения между явлениями. Для анализа здоровья населения и деятельности системы здравоохранения выделяют следующие группы относительных показателей:
- экстенсивные показатели;
- интенсивные показатели;
- показатели соотношения;
- показатели наглядности.
Экстенсивные показатели отражают внутреннюю структуру явления, разделение его на составные части, удельный вес каждой части в целом. К экстенсивным показателям относится структура заболеваемости, инвалидности, смертности, коечного фонда, врачебных специальностей и др. Экстенсивные коэффициенты характеризуют отношение части к целому, то есть определяют долю (удельный вес), процент части в целом, принятом за 100%. Используются для характеристики структуры статистической совокупности. Например: удельный вес (доля) заболеваний гриппом среди всех заболеваний в процентах; доля производственных травм среди всех травм у рабочих (отношение числа производственных травм к общему числу травм, умноженное на 100%). Рассчитывают показатель по следующей формуле (выражают в процентах):
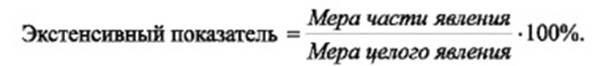
Интенсивные показатели характеризуют уровень, распространенность какого-либо явления в среде, непосредственно с ней связанного. Эти показатели рассчитывают, как правило, для анализа здоровья населения, где в качестве среды берут численность населения, а в качестве явления - число рождений, заболеваний, смертей и др. К интенсивным показателям относятся показатели заболеваемости, рождаемости, смертности населения и др. Интенсивные коэффициенты отражают частоту (уровень, распространенность) явления в однородной среде. На практике их применяют для оценки здоровья населения, медико-демографических процессов. Например: число случаев заболеваний с временной утратой трудоспособности на 100 работающих; число заболевших гипертонической болезнью на 1000 жителей; число родившихся на 1000 человек (определяется как отношение числа родившихся за год к средней численности населения административной территории, умноженное на 1000). Рассчитывают показатель по следующей формуле (выражают в промилле - 0/00, децимилле - 0/000или сантимилле - 0/0000):

Интенсивные коэффициенты бывают общие и специальные. При расчете общих интенсивных показателей за среду принимается численность населения в целом (показатель рождаемости, общий показатель смертности, показатель заболеваемости и др.). Специальные – вычисляют для отдельных групп населения: показатель плодовитости изучает число детей, родившихся на 1000 женщин детородного возраста, уровень заболеваемости гипертонической болезнью женщин-педагогов, повозрастной показатель смертности - число умерших в определенном возрасте и др.
Показатели соотношения характеризуют уровень (распространенность) какого-либо явления в среде, непосредственно (биологически) не связанного с данной средой. В этом их отличие от интенсивных показателей. Показатели соотношения рассчитывают для анализа деятельности системы здравоохранения, ее ресурсного обеспечения, где в качестве среды берут численность населения, а в качестве явления - количество врачей, средних медицинских работников, больничных коек, посещений амбулаторно-поликлинических учреждений и др. К показателям соотношения относится обеспеченность населения стационарной, амбулаторно-поликлинической помощью, врачами, средними медицинскими работниками и др. Рассчитывают показатель по следующей формуле (выражают в промилле - 0/00, децимилле - 0/000 или сантимилле -0/0000):

Показатели соотношения используются для характеристики обеспеченности уровня и качества медицинской помощью: число коек на 10000 человек; число врачей на 10000 жителей; число лекарственных препаратов, произведенных на 1000 жителей (отношение числа выпущенных лекарственных препаратов, к численности населения административной территории, умноженное на 1000).
Показатели наглядности применяют для анализа степени изменения изучаемого явления во времени. Эти показатели говорят о том, на сколько процентов или во сколько раз увеличились или уменьшились сравниваемые показатели за данный период времени. Рассчитывают показатель как отношение ряда сравниваемых величин к исходной величине, принятой за 100 или за 1, результат выражают либо в процентах, либо в долях. Как правило, за такую исходную величину берут начальные или конечные значения временного ряда.

Показатель наглядности можно выразить в разах, как отношение большего значения к меньшему, но в таком случае следует пояснить, происходит увеличение или уменьшение изучаемой величины.
Показатель наглядности применяется с целью более наглядного и доступного сравнения рядов абсолютных, относительных и средних величин. Коэффициент наглядности определяет, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых величин. Используется для характеристики динамики явления. При вычислении показателей наглядности одна из сравниваемых величин принимается за 100% или за единицу, а остальные величины с помощью пропорции пересчитываются в коэффициенты по отношению к этому числу. Чаще всего за 100% принимается первая исходная величина, но за 100 может быть принята величина и из середины, конца ряда. Например, число врачей в 2005 г. по сравнению с числом врачей в 2006 г., принятым за 100% (отношение числа специалистов в данном году к числу специалистов в предыдущем году, умноженное на 100%).
Абсолютные статистические показатели имеют определенные размерность и единицы измерения, показывают количество, численность чего-то или кого-то, например численность населения, количество больничных коек, врачей, родившихся, умерших людей и др.
Относительные статистические показатели более объективно выражают количественные соотношения между явлениями.
Абсолютные величины употребляют для характеристики:
§ абсолютных размеров явления в целом (показывают массовость явления);
§ редко встречающихся явлений (показывают единичность явления).
Виды абсолютных величин:
§ Индивидуальная абсолютная величина — характеризует единицу совокупности
§ Суммарная абсолютная величина — характеризует группу единиц или всю совокупность
Виды и методы расчета средних величин, их свойства и недостатки.
1. Средняя величина – это обобщающая характеристика размера изучаемого признака. Она позволяет одним числом количественно охарактеризовать качественно однородную совокупность.
Применение средних величин:
Для характеристики организации работы лечебно-профилактических учреждений и оценки их деятельности:
- в поликлинике (показатели нагрузки, среднее число детей на участке и т.д.);
- в стационаре (среднее число работы койки в году, средняя длительность заболевания и т.д.);
- в органах санэпиднадзора (средняя площадь на 1 человека, средние нормы питания и т.д.);
2. В демографических и медико-социальных исследованиях (средняя продолжительность предстоящей жизни и т.д.)
3. В медико-социальных исследованиях при изучении физического развития.
4. Для определения медико-физиологических показателей организма в норме и патологии в клинических и экспериментальных исследованиях.
Для расчета средних величин необходимо соблюдать следующие условия:
- средние величины должны быть рассчитаны на основе качественно однородных статистических групп;
- средние величины исчисляются на совокупностях, имеющих достаточно большое число наблюдений.
В медико-социальных исследованиях используются следующие виды средних величин:
- средняя арифметическая;
- средняя арифметическая взвешенная;
- средняя гармоническая взвешенная;
- средняя геометрическая невзвешенная;
- средняя геометрическая взвешенная;
- средняя квадратическая невзвешенная;
- средняя квадратическая взвешенная.
Виды средних величин: Мо – мода
Ме – медиана
М – средняя арифметическая
При изучении общественного здоровья, анализе деятельности учреждений здравоохранения, оценке работы медицинского персонала из всех видов средних величин наиболее часто используется средняя арифметическая, которая может быть простой и взвешенной.
Ряд наблюдений, все элементы которого упорядочены по возрастанию, называется вариационным рядом. Элемент вариационного ряда - варианта.
Средняя арифметическая простая - средняя вариационного ряда х1, х2,..., хn, где каждая варианта записана столько раз, сколько встречается. Вычисляется по формуле:
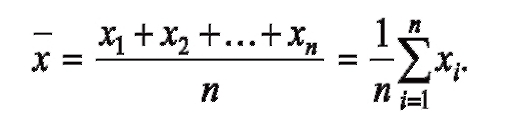
Среднюю арифметическую значений х 1, х 2, х? можно записать иначе, с учетом частоты повторений каждого из значений. Получаем среднюю арифметическую взвешенную вариационного ряда, где k различных значений k £ n.
Тогда средняя арифметическая взвешенная записывается как:
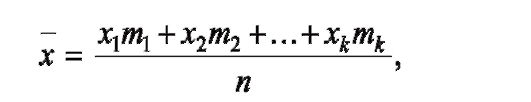
где каждое число mi - частота соответствующего значения xi, причем: m 1 + m 2 +...+ mk = n.
Формулу расчета средней арифметической взвешенной можно представить в следующем виде:
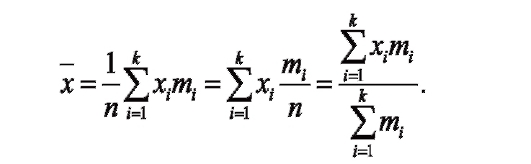
Средняя арифметическая простая и средняя арифметическая взвешенная - это одна и та же величина. Различие лишь в записи расчетной формулы.