69. ОСОБЕННОСТИ СТРАТЕГИЧЕСКОГО УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ОРГАНИЗАЦИЯМИ.
Содержание инновационной деятельности, ее характерные черты и особенности находят отражение в таком фундаментальном понятии, как понятие инновации.
Инновация (нововведение) – это конечный результат творческой деятельности, получивший воплощение в виде новой или усовершенствованной продукции, реализуемой на рынке, либо нового или усовершенствованного технологического процесса, используемого в практической деятельности.
Понятие «инновация» тесно связано с понятием «инновационный процесс».
Инновационный процесс представляет собой процесс создания и распространения нововведений (инноваций).
Понятие «инновационного процесса» шире понятия «инновации», т.к. собственно инновация (нововведение) является одним из компонентов инновационного процесса.
Основные компоненты инновационного процесса:
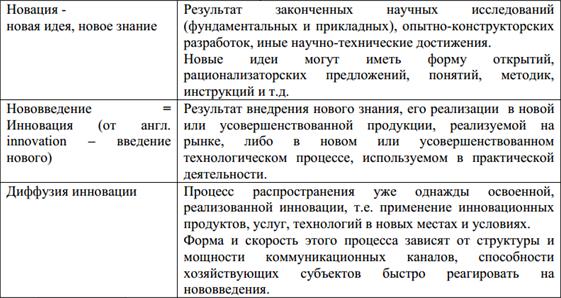
Множество организаций, субъектов инновационной деятельности, выполняющих функции обслуживания и содействия инновационным процессам, образуют инновационную инфраструктуру. Другими словами, инновационная инфраструктура - это организации и институты, способствующие осуществлению инновационной деятельности.
Инновационная инфраструктура - это множество субъектов инновационной деятельности, выполняющих функции обслуживания и содействия инновационным процессам.
По аналогии с транспортной инфраструктурой можно сказать, что инновационная инфраструктура - это все информационные, организационные, маркетинговые, образовательные и другие сети, которые помогают новой идее (как по «рельсам») добираться до своей практической реализации и находить своего потребителя.
|
|
Институты инновационной инфраструктуры призваны гармонизировать взаимосвязи между четырьмя основными типами рынков, определяющих эффективность функционирования инновационной системы, а именно: рынками инноваций как объектов интеллектуальной собственности, рынками инновационного капитала (под инновационным капиталом понимается капитал, связанный с финансированием инновационной деятельности и рынком цепных бумаг высокотехнологичных компаний), рынками инновационной продукции и рынками услуг по поддержке и сопровождению инновационной деятельности (рис. 3.1).
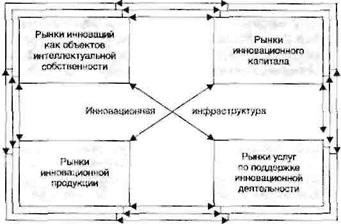
Рис. 3.1. Взаимосвязи основных инновационных рынков
В качестве наиболее актуальных задач развития инновационной инфраструктуры во многих странах в настоящее время рассматриваются:
• развитие производственно-технологической, информационной, экспертно-консалтинговой и образовательной инфраструктуры инновационной деятельности;
• образование финансовых институтов, обеспечивающих непрерывность финансирования инновационных проектов на всех стадиях инновационного цикла;
• содействие развитию кооперационных связей между субъектами инновационной системы.
Текущее состояние российской инновационной инфраструктуры характеризуется наличием ряда проблем, которые сдерживают и препятствуют эффективному развитию национальной инновационной системы в нашей стране. Так, существующая инновационная инфраструктура не способствует развитию кооперационных связей между субъектами инновационной системы: малые и средние инновационные компании крайне недостаточно интегрированы в инновационные сети; не развиты кооперационные связи, позволяющие формировать инновационные цепочки «наука и образование - инновационный малый и средний бизнес - крупный бизнес», что препятствует диффузии знаний, их распространению из сектора исследований и разработок, капитализации знаний в российской экономике. Без повышения эффективности инновационной инфраструктуры невозможно обеспечение трансфера результатов сектора исследований и разработок в российскую и глобальную экономику, развитие предпринимательства в инновационной сфере.
|
|
Ключевое значение для развития производственно-технологической, информационной, экспертно-консалтинговой и образовательной инфраструктуры инновационной деятельности играют технопарковые структуры.
Можно выделить три основные группы технопарковых стру ктур:
• инкубаторы;
• технопарки;
• технополисы.
Инкубаторы предназначены для «высиживания» новых инновационных предприятий, оказания им помощи на самых ранних стадиях их развития путем предоставления информационных, консультационных услуг, аренды помещения и оборудования, других услуг. Инкубатор занимает, как правило, одно или несколько зданий. Инкубационный период фирмы-клиента длится обычно от 2 до 5 лет, после чего инновационная фирма покидает инкубатор и начинает самостоятельную деятельность.
Наибольшее распространение инкубаторы но «выращиванию» новых бизнес-единиц получили в США (в настоящее время в этой стране насчитывается около 600 инкубаторов, объединенных в Национальную ассоциацию инкубаторов бизнеса). Несмотря на большой разброс направлений деятельности инкубаторных структур (например, созданы инкубаторы искусств и сельскохозяйственные инкубаторы), их различную специализацию (например, существуют инкубаторы для инновационного предпринимательства только в области программного обеспечения или только в области биотехнологии), почти три четверти всех инкубаторов в этой стране поддерживают самые тесные отношения с ближайшими университетами, привлекая их персонал и мощности для оказания услуге целью формирования и выживания малого бизнеса, повышения социальной и экономической активности населения, развития инновационной среды.
|
|
Технопарки - научно-производственный территориальный комплекс, главная задача которого состоит в формировании максимально благоприятной среды для развития малых и средних наукоемких инновационных фирм-клиентов.
Основной структурной единицей технопарка является центр. Обычно в структуре технопарка представлены:
• инновационно-технологический центр;
• учебный центр:
• консультационный центр;
• информационный центр;
• маркетинговый и другие центры;
• промышленная зона.
Центральное место в структуре технопарка обычно отводится инновационно-технологическим центрам (ИТЦ), при которых нередко функционируют информационно-аналитические центры. Подобно инкубаторам, ИТЦ может являться и самостоятельным элементом инновационной инфраструктуры, функционирующим независимо от какой-либо технопарковой структуры.
Первый российский технопарк был создан в Томске в 1990 т. В настоящее время это - Открытое акционерное общество «Томский международный деловой центр "Технопарк"».
Первым российским парком, созданным на основе университета, стал научный парк при Московском государственном университете им. М.В. Ломоносова. При создании в 1992 г. он представлял собой просто инновационно-технологический центр.
В настоящее время достаточно успешно функционируют и многие другие российские технопарки. Так, на базе Российского научного центра «Курчатовский институт» (РНЦ КИ) был образован технопарк «Курчатовский» (г. Москва). Уникальные технологии и научно-технические разработки этого технопарка, высокий потенциал специалистов являются важными предпосылками его успешного функционирования. Кроме того, ключевыми факторами успеха и развития этого технопарка являются развитая энергетическая и социально-бытовая инфраструктура РНЦ КИ, наличие свободных производственных и офисных помещений, отдельная охраняемая территория, а также предыдущий опыт создания и развития средних и малых предприятий.
Технополис, который нередко называют также научным городом или наукоградом, «городом мозгов», представляет собой крупный современный научно-промышленный комплекс, включающий университет или другие вузы, научно-исследовательские институты, а также жилые районы, оснащенные культурной и рекреационной инфраструктурой.
К примерам наиболее успешно развивающихся технополисов многие специалисты относят такие города и территориальные образования, как Тампере в Финляндии, Валлес в Испании, Энсхеде в Голландии, Шеффилд и Кембридж в Великобритании, Цукуба, Тояма, Оита и Кумамото в Японии, Силиконовая Долина и Бостонский маршрут 128 в США, Шеньчжень и Наньху в Китае, Лейвен и Льеж в Бельгии и многие другие.
КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ И МАТЕМАТИЧЕСКИЕ МЕТОДЫВ УПРАВЛЕНИИ
71.МАТЕМАТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫВ УПРАВЛЕНИИ ОРГАНИЗАЦИЕЙ.
Моделирование – способ отображения объективной реальности, при котором для изучения оригинала применяется специально построенная модель, воспроизводящая определенные (как правило, лишь существенные) свойства исследуемого реального явления (процесса).
Главные функции модели - упрощение получения информации о свойствах объекта; передача информации и знаний; управление и оптимизация объектами и процессами; прогнозирование; диагностика.
Преимущества математических моделей:
1. Более структурировано и компактно представляют необходимую информацию;
2. Формализуют ряд управленческих процессов, обосновывая выбор альтернатив.
Пример моделей
1. Теория игр – метод моделирования оценки воздействия принятого решения на конкурентов. Редко используется, поскольку ситуации реального мира сложны и их сложно прогнозировать. Но она полезна для выделения наиболее важных и требующих учёта факторов и ситуаций принятия решений в условиях конкурентной борьбы. Как это выглядит? Думаю, все помнят матрицы шикина в применении к дилемме узника? Кто нет – дружно "фейсом об бук". Примеры использования: изменение цен, модификация и запуск новой продукции и т.д.
2. Модели теории очередей (оптимального обслуживания) – для определения оптимального числа каналов обслуживания по отношению к потребности на них. Проблема выбора между уравновешиванием расходов на дополнительные каналы обслуживания и потерь от обслуживания на уровне ниже оптимального. Оптимум каналов нам нужен для уравновешивания случаев с чрезмерно малым или большим количеством потребителей. Пример из Шикина: количество касс в Пятёрочке, время, которое человек готов выстоять в очереди. Другие примеры: количество операторов справочной службы, количество мастеров по ремонту мобилок (и др. оборудования) и предел терпения людей-клиентов и т.д.
3. Модели управления запасами – используется для определения времени размещения заказов на ресурсы и их количества, а также массы готовой продукции на складах. Резерв на складах необходим для недопущения задержек в поставках. Цель модели в сведении к минимуму отрицательных последствий накопления запасов, что выражается в издержках: (1) на размещение заказов, (2) на хранение и (3) на выплату неустойки в случае срыва поставки, если не хватило товаров на складе, простой оборудования и трудовых кадров. С другой стороны "затоваривание" складов приводит к снижению оборотных средств.
4. Модель линейного программирования – для определения оптимального распределения дефицитных (ограниченных) ресурсов при наличии конкурирующих потребностей. Очень популярны на промышленных предприятиях. Используются штабным руководством для разрешения производственных трудностей. Примеры: планирование ассортимента изделий, определение оптимального расположения нового завода, распределение рабочих и т.д.
5. Имитационное моделирование – (в узком смысле, поскольку все предыдущие модели были также имитационными, но в широком смысле) – используется в слишком сложных для мат. моделирования ситуациях: (1) чрезмерно большое количество переменных, (2) трудность мат анализа зависимостей между переменными, (3) высокая степень неопределённости. Позволяет делать эксперименты и выбирать альтернативы. Примеры использования: определение объёма сбыта в связи с изменением цен или рекламы продукции, ожидаемого прироста производительности и прибыльности в связи с применением новой технологии.
6. Экономический анализ – часто не осознаётся моделированием, но является таковым. Вбирает в себя почти все методы оценки издержек и эконом. выгод и относительной безубыточности предприятия. Пример: точка безубыточности: общий доход=суммарные издержки. Используются в фин.мене и бухучёте. Большинство методов бухучёта основано на моделях эк. Анализа
Общие проблемы моделирования:
- Недостоверные исходные допущения или предпосылки. Некоторые предпосылки не поддаются оценке и их нельзя объективно проверить. Если много ненадёжных предпосылок, то использование модели усложнено. Также важны связи, между переменными в модели и их точность.
- Информационные ограничения. Не всю информацию можно получить в необходимом объёме. Также есть сложноформализуемые параметры. Т.е. проблема неопределённости ставит под вопрос о целесообразности использования модели вообще. Иногда лучше положиться на интуицию, опыт или помощь консультантов.
- Страх пользователей. ЛПР не понимают модель и бояться её применять, у них не хватает знаний! Поэтому разработчики моделей должны обучить ЛПР использованию модели. А руководству нужно приводить примеры эффективности таких моделей.
- Слабое использование на практике. Причины: страх, непонимание и сопротивление переменам. Проблема частично снижается вовлечением линейного руководства в процесс разработки модели (т.к. её разработкой чаще всего занято штабное руководство).
- Чрезмерная стоимость. Учёт всех издержек включает время на создание, обучение и сама стоимость разработки. Стоит ли начинка выделки?
Основные этапы разрешения проблемы принятия решения:
1. Сформулировать проблему (определение реальной проблемы, а не ее симптомов)
2. Выбрать модель (если готовой модели нет, необходимо ее создать). Шикин говорит именно о математических моделях и выделяет среди них 3:
Ø Детерминированные (при их разработке исходят из той предпосылки, что основные факторы, характеризующие ситуацию, вполне определенны и известны. Здесь обычно ставится задача оптимизации некоторой величины (например, минимизация затрат)). На мой взгляд, можно вспомнить:
Графы и сети – построены на графическом решении управленческих проблем. Графы состоят из вершин и рёбер, их соединяющих. При помощи связанных графов строят маршруты: они могут быть цепью, если каждое ребро графа встречается в нём не более 1 раза, а могут быть циклом, если начало и конец маршрута совпадают. Используется для обустройства худ. выставок, проложения транспортных маршрутов доставки и т.д. Сети – это графы в их практическом приложении. Примеры: древо решений, расчёт максимального потока (транспортной сети, к примеру), нахождение кратчайшего маршрута, построение "критического пути" для планирования осуществления проекта: последовательность действий и их временные затраты.
Критический путь: анализ проекта с точки зрения минимальных временнЫх затрат на его выполнение. Для этого проект разбивают на отдельные работы, оценивают время, необходимое на проведение каждой из них, и записывают последовательность операций, показывающую, какие работы должны быть закончены, прежде чем начнутся другие. Затем вычерчивается диаграмма работ, на которой каждая работа изображается направленным ребром, и определяется критический путь, имеющий наибольшую общую продолжительность. Он и определяет минимум временнЫх затрат на выполнение проекта (в учебнике рассмотрен пример строительства загородного дома).
Выстраивание иерархий и приоритетов – достигается путём попарного сравнения имеющихся совокупностей (вариантов решений) и составлением матриц. Приведем пример типичной иерархии. Первый уровень иерархии имеет одну цель: общее благосостояние страны. Второй уровень иерархии имеет три цели: сильную экономику, здравоохранение, национальную оборону. Приоритеты этих целей получаются из матрицы попарных сравнений относительно цели первого уровня. Целями третьего уровня являются отрасли промышленности. Задача заключается в определении влияния отраслей промышленности на общее благосостояние страны через промежуточный второй уровень. Поэтому приоритеты отраслей промышленности относительно каждой цели второго уровня получаются из матриц попарных сравнений относительно этих целей, а полученные столбцы приоритетов взвешиваются затем при помощи столбца приоритетов второго уровня, что позволяет получить в итоге искомый составной столбец приоритетов отраслей промышленности.
Линейные задачи:
- о выпуске продукции: выбрать такое количество разных продуктов для производство, чтобы максимизировать прибыль и минимизировать затраты на ресурсы.
- транспортная задача: минимизация стоимости перевозки известного кол-ва товаров
Управление запасами:
- модель производственных поставок
-модель поставок со скидками
Модель Леонтьева: отражает потенциальные возможности, которые заложены в технологии производства; учитывает материальные ресурсы отрасли и трудовые ресурсы.
Оптимуму по Парето – применяется в многокритераиальных задачах, когда нам нужно удовлетворить сразу 2 (или больше) требования хотя бы в какой-то степени. Среди известных стоит отметить два: 1 ) метод уступок и 2) метод идеальной точки. Оба метода используют множество Парето, составленное в данном случае из допустимых точек задачи, которые не могут быть "сдвинуты" в пределах допустимого множества с улучшением сразу по обоим критериям. Иными словами, улучшая значения одного из критериев, мы неизбежно ухудшаем значения другого. Метод (последовательных) уступок заключается в том, что лицо, принимающее решение (ЛПР), работая в режиме диалога со специалистом, анализирует точки на границе Парето и в конце концов соглашается остановиться на некоторой компромиссной. Метод идеальной точки состоит в отыскании на границе Парето точки, ближайшей к точке утопии, задаваемой ЛПР. Обычно ЛПР формулирует цель в виде желаемых значений показателей, и часто в качестве координат целевой точки выбирается сочетание наилучших значений всех критериев (обычно эта точка не реализуется при заданных ограничениях, поэтому ее и называют точкой утопии).
Методы прогнозирования:
1) Качественные – использование мнений экспертов (Дельфи, метод исторических аналогий и т.д.)
2) Количественные – обработка числовых массивов данных:
· Каузальные (причинно-следственные)
· Методы анализа временных рядов. Временной ряд – последовательность значений некоторого показателя во времени (например, объемов продаж). Часто используется метод проецирования тренда – построение прямой, которая «в среднем» наименее уклоняется от массива точек, заданного временным рядом.
Ø Стохастические (применяются в тех случаях, когда некоторые факторы носят неопределенный, случайный характер). На мой взгляд, можно вспомнить:
про классическую вероятность: если n – число всех равновозможных исходов, а m – число исходов, составляющих событие А, то вероятность события А (p(A)) определяется следующим образом: p(A)=m/n. Пример: Бросается игральный кубик. Исходов будет 6: «выпало число 1», «выпало число 2», …, «выпало число 6». Значит вероятность выпадания каждого из этих чисел равно 1/6.
Ø Игровые (применяются при наличии противников или союзников с собственными интересами, например, переговоры). На мой взгляд, можно вспомнить Дилемму узников: 2 узника находятся в предварительном заключении по подозрению в совершении преступления. Если оба будут молчать, то наказанием будет лишь срок предварительного заключения (потери каждого из узников составят (-1)). Если сознаются, то получат срок, учитывающий признание как смягчающее обстоятельство (потери каждого из узников составят в этом случае (-6)). Если же заговорит только один из узников, а другой будет молчать, то в этом случае заговоривший будет выпущен на свободу (его потери равны 0), а сохраняющий молчание получит максимально возможное наказание (-9).
3. Найти решение (для поиска решения необходимы конкретные данные, сбор и подготовка которых требуют, как правило, значительных совокупных усилий, и их (данные) часто приходится преобразовывать к виду, соответствующему выбранной модели)
4. Тестировать решение (по результатам теста либо усовершенствовать, либо заменить модель, если не устраивает)
5. Организовать контроль за правильным использованием модели (соблюдение ограничений, предполагаемых моделью, качества входных данных и получаемого решения).
6. Создать режим благоприятствования (трудно, т.к. внедрение новаций часто наталкивается на незаинтересованность и даже сопротивление, поэтому надо обучать персонал, учитывать разнообразие поведенческих мотивов людей).
УПРАВЛЕНИЕ ПЕРСОНАЛОМ