1.1. Дана система векторов: 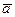 ,
,  ,
,  ,
,  . Найти какой-нибудь базис этой системы векторов и все векторы системы, не входящие в этот базис, выразить через векторы базиса.
. Найти какой-нибудь базис этой системы векторов и все векторы системы, не входящие в этот базис, выразить через векторы базиса.
Общие сведения. Базисом называют:
1*. На прямой: любой ненулевой вектор  . Всякий вектор
. Всякий вектор  , лежащий на этой прямой, может быть представлен в виде:
, лежащий на этой прямой, может быть представлен в виде:  =
= 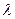 ·
·  , число
, число 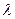 – координата относительно этого базиса.
– координата относительно этого базиса.
2*. На плоскости: любая пара неколлинеарных векторов  ,
,  . Всякий вектор
. Всякий вектор  , лежащий в этой плоскости, может быть представлен в виде:
, лежащий в этой плоскости, может быть представлен в виде:  =
= 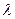 ·
·  +
+ 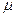 ·
·  , числа
, числа 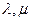 – координаты относительно этого базиса.
– координаты относительно этого базиса.
3*. В пространстве: любые три вектора  ,
,  ,
,  , если они не компланарны. Всякий вектор
, если они не компланарны. Всякий вектор 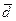 пространства может быть представлен в виде линейной комбинации векторов базиса:
пространства может быть представлен в виде линейной комбинации векторов базиса:  =
= 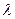 ·
·  +
+ 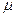 ·
·  +
+ 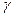 ·
·  , где
, где 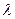 ,
, 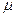 ,
, 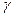 – координаты вектора
– координаты вектора  относительно этого базиса.
относительно этого базиса.
Так как пространство можно рассматривать как общий случай 3-мерного пространства, а плоскость и прямую как частные случаи, то решать задачу будем для 3-мерных векторов.
Общая схема решения задачи:
1). Проверяем признак наличия базиса в заданной совокупности векторов.
2). Если базис выделен, записываем линейную комбинацию:  =
= 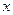 ·
·  +
+ 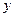 ·
·  +
+ 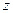 ·
·  .
.
3). Решая систему уравнений, вычисляем неизвестные: 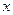 ,
, 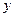 ,
, 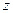 .
.
4). Оформляем ответ.
Примеры (и образец оформления):
Пример- 1*: Заданы векторы:  =(1),
=(1),  =(3),
=(3),  =(2). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
=(2). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
Решение:
1). Проверяем признак наличия базиса в заданной совокупности векторов. Так как из записи векторов следует, что все они принадлежат некоторой прямой, то признаком существования базиса является присутствие в совокупности векторов 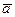 ,
,  ,
,  ненулевого вектора.
ненулевого вектора.
2). В качестве базиса примем вектор  . Тогда можем записать:
. Тогда можем записать:  =
= 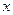 ·
·  ,
,  =
= 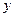 ·
·  .
.
3). Решаем уравнения: (3)= 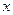 ·(1); (2)=
·(1); (2)= 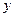 ·(1), то есть уравнения: 3 =
·(1), то есть уравнения: 3 = 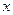 ·1; 2 =
·1; 2 = 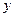 ·1, из чего следует:
·1, из чего следует: 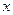 =3;
=3; 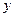 =2.
=2.
Ответ: один из базисов:  ; тогда:
; тогда:  =3
=3  ,
,  =2
=2  .
.
Пример- 2*: Заданы векторы:  =(1,2),
=(1,2),  =(3,1),
=(3,1),  =(2,3). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
=(2,3). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
Решение:
1). Проверяем признак наличия базиса в заданной совокупности векторов. Так как из записи векторов следует, что все они принадлежат некоторой плоскости, то признаком существования базиса является наличие в совокупности векторов 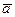 ,
,  ,
,  хотя бы двух неколлинеарных векторов. В нашем случае среди заданных векторов нет коллинеарных. Это значит: любая пара векторов из заданной совокупности векторов может быть принята в качестве базиса.
хотя бы двух неколлинеарных векторов. В нашем случае среди заданных векторов нет коллинеарных. Это значит: любая пара векторов из заданной совокупности векторов может быть принята в качестве базиса.
2). В качестве базиса примем векторы  и
и  . Тогда можем записать:
. Тогда можем записать:  =
= 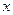 ·
·  +
+ 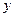 ·
·  , то есть:
, то есть: 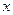 ·(1,2)+
·(1,2)+ 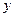 · (3,1)=(2,3). Используя свойства линейных операций с векторами, представим последнее равенство в виде: (
· (3,1)=(2,3). Используя свойства линейных операций с векторами, представим последнее равенство в виде: (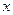 ·1+
·1+ 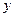 ·3;
·3; 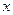 ·2+
·2+ 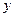 ·1)= (2,3), или в виде системы уравнений:
·1)= (2,3), или в виде системы уравнений:
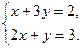
3). Решение системы уравнений: 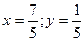 . Тогда можем записать:
. Тогда можем записать:  =
= 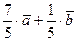 .
.
Ответ: один из базисов: 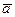 ,
,  ; тогда:
; тогда:  =
= 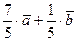 .
.
Пример- 3*: Заданы векторы:  =(3,1,2),
=(3,1,2),  =(1,3,1),
=(1,3,1),  =(-1,2,4),
=(-1,2,4),  =(-2,4,7). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
=(-2,4,7). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
Решение:
1). Проверяем признак наличия базиса в заданной совокупности векторов. Так как из записи векторов следует, что все они принадлежат некоторому пространству, то признаком существования базиса является наличие в совокупности векторов 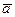 ,
,  ,
,  ,
,  хотя бы трёх некомпланарных векторов. Так как векторы
хотя бы трёх некомпланарных векторов. Так как векторы 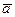 ,
,  неколлинеарные, то будем проверять тройки векторов
неколлинеарные, то будем проверять тройки векторов 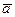 ,
,  ,
,  и
и 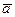 ,
,  ,
,  , используя понятие смешанного произведения:
, используя понятие смешанного произведения:
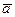

 =
= 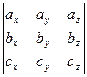 =
= 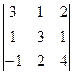 = 35
= 35 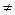 0,
0, 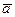

 =
= 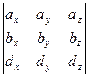 =
= 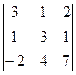 = -40
= -40 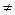 0.
0.
2). В качестве базиса может быть принята любая из троек векторов из заданной системы векторов. Примем в качестве базиса тройку векторы 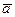 ,
,  ,
,  . Тогда можем записать:
. Тогда можем записать:  =
= 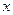 ·
·  +
+ 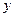 ·
·  +
+ 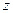 ·
·  , то есть:
, то есть: 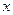 ·(3,1,2)+
·(3,1,2)+ 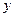 ·(1,3,1)+
·(1,3,1)+ 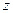 ·(-1,2,4)=(-2,4,7). Используя свойства линейных операций с векторами, представим последнее равенство в виде: (
·(-1,2,4)=(-2,4,7). Используя свойства линейных операций с векторами, представим последнее равенство в виде: (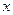 ·3+
·3+ 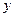 ·1–
·1– 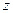 ·1;
·1; 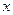 ·1+
·1+ 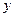 ·3+
·3+ 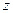 ·2;
·2; 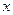 ·2+
·2+ 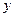 ·1+
·1+ 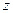 ·4)=(-2,4,7), или в виде системы уравнений:
·4)=(-2,4,7), или в виде системы уравнений:
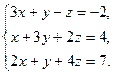
3). Решение системы: 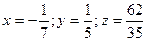 . Тогда можем записать:
. Тогда можем записать:  =
= 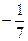 ·
·  +
+ 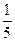 ·
·  +
+ 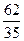 ·
·  .
.
Ответ: один из базисов: 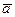 ,
,  ,
,  ; тогда:
; тогда:  =
= 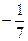 ·
·  +
+ 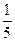 ·
·  +
+ 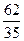 ·
·  .
.
Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов) обязательно!
Варианты индивидуальных заданий:
| Вар. | Задание: | Вар. | Задание: |
| 1. |  =(3,1,2), =(3,1,2),  =(1,3,1), =(1,3,1),  =(-1,2,4), =(-1,2,4),  =(-2,4,7). =(-2,4,7).
| 16. |  =(2,3,1), =(2,3,1),  =(2,2,3), =(2,2,3),  =(4,1,2), =(4,1,2),  =(8,0,5). =(8,0,5).
|
| 2. |  =(1,3,0), =(1,3,0),  =(2,-1,1), =(2,-1,1),  =(1,-1,2), =(1,-1,2),  =(6,12,-1). =(6,12,-1).
| 17. |  =(4,2,3), =(4,2,3),  =(3,2,-1), =(3,2,-1),  =(4,1,2), =(4,1,2),  =(3,1,8). =(3,1,8).
|
| 3. |  =(2,1,-1), =(2,1,-1),  =(4,3,2), =(4,3,2),  =(1,-1,1), =(1,-1,1),  =(1,-4,4). =(1,-4,4).
| 18. |  =(1,2,-1), =(1,2,-1),  =(3,0,2), =(3,0,2),  =(-1,1,1), =(-1,1,1),  =(8,1,12). =(8,1,12).
|
| 4. |  =(4,1,1), =(4,1,1),  =(2,-1,-3), =(2,-1,-3),  =(-1,2,1), =(-1,2,1),  =(-9,5,5). =(-9,5,5).
| 19. |  =(1,4,1), =(1,4,1),  =(-3,2,0), =(-3,2,0),  =(1,-1,2), =(1,-1,2),  =(-9,-8,-3). =(-9,-8,-3).
|
| 5. |  =(-2,3,1), =(-2,3,1),  =(1,3,-1), =(1,3,-1),  =(2,4,1), =(2,4,1),  =(-5,-5,5). =(-5,-5,5).
| 20. |  =(2,1,-2), =(2,1,-2),  =(3,-1,1), =(3,-1,1),  =(4,1,0), =(4,1,0),  =(-5,9,-13). =(-5,9,-13).
|
| 6. |  =(5,1,1), =(5,1,1),  =(2,-1,3), =(2,-1,3),  =(1,2,-1), =(1,2,-1),  =(13,,7). =(13,,7).
| 21. |  =(0,5,1), =(0,5,1),  =(3,2,-1), =(3,2,-1),  =(-1,1,0), =(-1,1,0),  =(-15,5,6). =(-15,5,6).
|
| 7. |  =(3,2,1), =(3,2,1),  =(-2,2,1), =(-2,2,1),  =(3,1,-1), =(3,1,-1),  =(6,12,-1). =(6,12,-1).
| 22. |  =(2,2,-1), =(2,2,-1),  =(0,-2,1), =(0,-2,1),  =(1,3,1), =(1,3,1),  =(8,9,4). =(8,9,4).
|
| 8. |  =(3,1,2), =(3,1,2),  =(2,1,1), =(2,1,1),  =(2,-1,4), =(2,-1,4),  =(3,-3,4). =(3,-3,4).
| 23. |  =(2,2,1), =(2,2,1),  =(1,-2,0), =(1,-2,0),  =(-3,2,5), =(-3,2,5),  =(3,-4,0). =(3,-4,0).
|
| 9. |  =(4,2,1), =(4,2,1),  =(-1,2,1), =(-1,2,1),  =(-1,1,2), =(-1,1,2),  =(3,3,-1). =(3,3,-1).
| 24. |  =(2,1,3), =(2,1,3),  =(3,5,3), =(3,5,3),  =(4,2,1), =(4,2,1),  =(3,1,3). =(3,1,3).
|
| 10. |  =(-1,2,1), =(-1,2,1),  =(2,1,3), =(2,1,3),  =(1,1,-1), =(1,1,-1),  =(-1,7,4). =(-1,7,4).
| 25. |  =(2,3,1), =(2,3,1),  =(1,-1,2), =(1,-1,2),  =(2,-1,0), =(2,-1,0),  =(-1,7,0). =(-1,7,0).
|
| 11. |  =(1,1,4), =(1,1,4),  =(0,-3,2), =(0,-3,2),  =(2,1,-1), =(2,1,-1),  =(6,5,-14). =(6,5,-14).
| 26. |  =(1,-1,2), =(1,-1,2),  =(3,2,0), =(3,2,0),  =(-1,1,1), =(-1,1,1),  =(11,-1,4). =(11,-1,4).
|
| 12. |  =(1,-2,0), =(1,-2,0),  =(1,1,3), =(1,1,3),  =(1,1,4), =(1,1,4),  =(6,-1,7). =(6,-1,7).
| 27. |  =(-1,1,2), =(-1,1,2),  =(0,3,2), =(0,3,2),  =(1,-1,1), =(1,-1,1),  =(1,3,-1). =(1,3,-1).
|
| 13. |  =(1,0,5), =(1,0,5),  =(-1,3,2), =(-1,3,2),  =(1,-1,1), =(1,-1,1),  =(5,15,0). =(5,15,0).
| 28. |  =(2,1,3), =(2,1,3),  =(-1,0,4), =(-1,0,4),  =(3,2,4), =(3,2,4),  =(4,1,3). =(4,1,3).
|
| 14. |  =(1,3,2), =(1,3,2),  =(0,-1,2), =(0,-1,2),  =(3,3,4), =(3,3,4),  =(2,-1,11). =(2,-1,11).
| 29. |  =(-3,2,4), =(-3,2,4),  =(-2,0,1), =(-2,0,1),  =(2,3,1), =(2,3,1),  =(3,-2,0). =(3,-2,0).
|
| 15. |  =(1,-1,2), =(1,-1,2),  =(-1,0,1), =(-1,0,1),  =(2,5,-3), =(2,5,-3),  =(11,5,-3). =(11,5,-3).
| 30. |  =(5,1,3), =(5,1,3),  =(0,1,2), =(0,1,2),  =(-1,1,1), =(-1,1,1),  =(1,1,1). =(1,1,1).
|
1.2. Заданы точки A, B, C, D в правой системе координат. Вычислить указанные в заданиях величины с точностью 0.001.
а) проекцию вектора 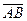 на вектор
на вектор 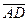 ;
;
б) площадь треугольника ABC;
в) объём тетраэдра 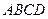 .
.
Общие сведения: по всем представленным заданиям:
1). Для удобства применения необходимых выражений обозначим: A = 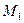 , B =
, B = 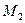 , C =
, C = 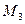 , D =
, D = 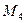 . Тогда можем записать выражения для векторов, используемые во всех названных задачах:
. Тогда можем записать выражения для векторов, используемые во всех названных задачах: 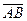 = B–A =
= B–A = 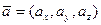 =
= 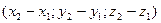 ;
;
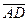 = D–A =
= D–A = 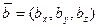 =
= 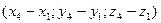 .
.
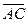 = C–A =
= C–A = 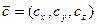 =
= 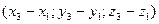 .
.
2). Теперь приступим к решению задач, применяя формулы из общей теории.
а)*. Заданы векторы  и
и  . Требуется найти проекцию вектора
. Требуется найти проекцию вектора  на направление, определяемое вектором
на направление, определяемое вектором  . Из выражения для скалярного произведения заданных векторов:
. Из выражения для скалярного произведения заданных векторов: 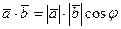 проекция вектора
проекция вектора  на направление
на направление  может быть вычислена по формуле:
может быть вычислена по формуле: 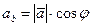 =
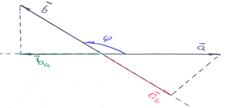
= 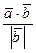 . Рисунки иллюстрируют формулы:
. Рисунки иллюстрируют формулы:
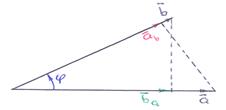
| 
|
Для векторов, заданных в координатной форме, запишем необходимые для вычисления 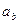 выражения:
выражения:
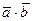 =
= 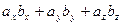 ;
; 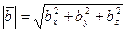
б)*. Заданы векторы  и
и  . Требуется найти площадь треугольника, образованного векторами
. Требуется найти площадь треугольника, образованного векторами  и
и  . Известно, что площадь параллелограмма, заданного векторами
. Известно, что площадь параллелограмма, заданного векторами  и
и  , определяется выражением:
, определяется выражением: 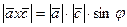 , где
, где 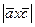 – модуль векторного произведения векторов
– модуль векторного произведения векторов  и
и  . Для решаемой задачи это значит, что площадь треугольника, построенного на векторах
. Для решаемой задачи это значит, что площадь треугольника, построенного на векторах  и
и  , можно вычислять по формуле:
, можно вычислять по формуле:
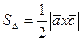 , где
, где  =
= 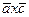 =
= 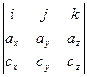 =
= 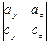 ∙
∙ 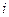 –
– 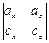 ∙ j +
∙ j + 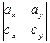 ∙ k,
∙ k,
где 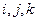 – единичные векторы, определяющие направления осей правой прямоугольной системы координат
– единичные векторы, определяющие направления осей правой прямоугольной системы координат 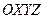 .
.
в)*. При вычислении объёма 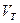 тетраэдра важно вспомнить, что
тетраэдра важно вспомнить, что 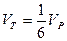 , где
, где 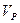 – объём параллелепипеда. В задании требуется вычислить объём
– объём параллелепипеда. В задании требуется вычислить объём 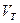 , определяемого тремя векторами
, определяемого тремя векторами  ,
,  ,
,  . Но этими же векторами определяется параллелепипед, объём которого вычисляется при помощи смешанного (векторно-скалярного) произведения этих векторов. Для иллюстрации используемых при решении задачи формул удобно привести все векторы к общей точке: так как векторы свободные, то от этого они не изменяются. На рисунке показаны все участвующие в формулах элементы.
. Но этими же векторами определяется параллелепипед, объём которого вычисляется при помощи смешанного (векторно-скалярного) произведения этих векторов. Для иллюстрации используемых при решении задачи формул удобно привести все векторы к общей точке: так как векторы свободные, то от этого они не изменяются. На рисунке показаны все участвующие в формулах элементы.
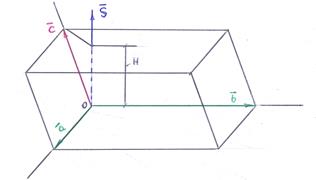 Имеем: (
Имеем: (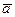 x
x  )∙
)∙  =
= 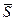 ∙
∙  =
= 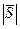 ∙
∙ 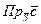 =
= 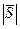 ∙
∙ 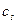 , где |
, где | 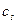 |=H, причём
|=H, причём 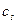 =H, если тройка векторов – правая и
=H, если тройка векторов – правая и 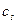 =–H, если – левая. Из этой формулы следует: (
=–H, если – левая. Из этой формулы следует: (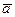 x
x  )∙
)∙  = V – объём параллелепипеда, но со знаком.
= V – объём параллелепипеда, но со знаком.
Так как в задании требуется вычислить только объём, то независимо от того, какая тройка используется в вариантах задания, все используют формулу: |(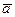 x
x  )∙
)∙  |=| V |.
|=| V |.
Итак, имеем векторы 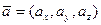 ,
, 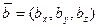 ,
, 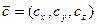 . Вычисляем:
. Вычисляем:
(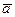 x
x  )∙
)∙  =
= 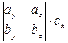 –
– 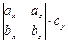 +
+ 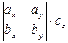 =
= 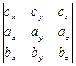 =
= 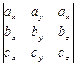 .
.
Записываем окончательную формулу: 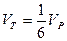 =
= 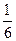 |(
|(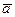 x
x  )∙
)∙  |.
|.
Примеры (и образец оформления):
Общая часть. Пусть имеем точки A = 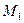 =(1,2,0), B =
=(1,2,0), B = 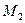 =(1,1,2), C =
=(1,1,2), C = 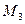 =(2,3,1), D =
=(2,3,1), D = 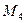 =(0,1,-1). Построим векторы:
=(0,1,-1). Построим векторы: 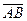 = B–A =
= B–A = 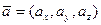 =
= 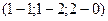 = (0,-1, 2);
= (0,-1, 2);
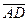 = D–A =
= D–A = 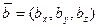 =
= 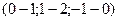 =(-1,-1,-1).
=(-1,-1,-1).
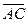 = C–A =
= C–A = 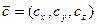 =
= 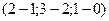 =(1,1,1);
=(1,1,1);
2). Теперь приступим к решению задач, применяя необходимые формулы.
Пример- а)*: Используем полученные векторы:  =(0,-1,2),
=(0,-1,2),  =(-1,-1,-1). Требуется найти проекцию вектора
=(-1,-1,-1). Требуется найти проекцию вектора  на направление, определяемое вектором
на направление, определяемое вектором  .
.
Решение:
1). Воспользуемся формулой: 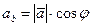 =
= 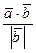 .
.
2). Вычислим: 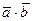 =
= 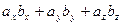 =
= 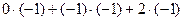 =–1.
=–1.
3). Вычислим: 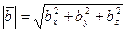 =
= 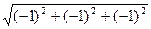 =
= 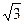 .
.
4). Вычислим: 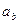 =
= 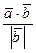 =
= 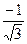 =–
=– 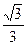 =–0.577350269... При заданной точности вычислений примем:
=–0.577350269... При заданной точности вычислений примем: 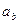 =–0.577.
=–0.577.
Ответ: 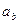 =–0.577.
=–0.577.
Пример- б)*: Используем полученные векторы:  =(0,-1,2),
=(0,-1,2),  =(1,1,1). Требуется найти площадь треугольника, образованного векторами
=(1,1,1). Требуется найти площадь треугольника, образованного векторами  и
и  .
.
Решение:
1). Общая формула: 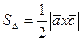 , где
, где  =
= 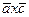 =
= 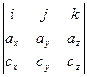 =
= 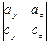 ∙
∙ 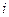 –
– 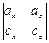 ∙
∙ 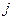 +
+ 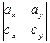 ∙
∙ 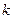 .
.
2). Вычислим:  =
= 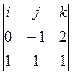 =
= 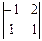 ∙
∙ 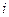 –
– 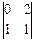 ∙
∙ 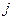 +
+ 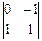 ∙
∙ 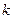 = –3
= –3 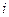 +2
+2 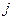 –
– 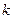 .
.
3). Вычислим: 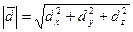 =
= 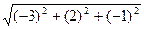 =
= 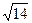 .
.
4). Вычислим: 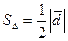 =
= 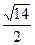 =1.87082869... При заданной точности вычислений примем:
=1.87082869... При заданной точности вычислений примем: 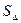 =1.871.
=1.871.
Ответ: 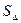 =1.871.
=1.871.
Пример- в)*: Заданы векторы:  =(0,-1,2),
=(0,-1,2),  =(-1,-1,-1),
=(-1,-1,-1),  =(1,1,1). В задании требуется вычислить объём тетраэдра
=(1,1,1). В задании требуется вычислить объём тетраэдра 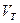 , определяемого тремя векторами
, определяемого тремя векторами  ,
,  ,
,  .
.
Решение:
1). Общая формула: 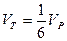 =
= 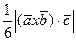 .
.
2). Вычислим: 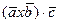 =
= 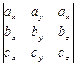 =
= 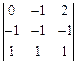 =0 – векторы
=0 – векторы  ,
,  ,
,  компланарны.
компланарны.
3). Вычислим: |(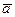 x
x  )∙
)∙  |=0.
|=0.
4). Вычислим: 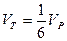 =0. При заданной точности вычислений примем:
=0. При заданной точности вычислений примем: 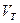 =0.000.
=0.000.
Ответ: 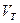 =0.000.
=0.000.
Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов) обязательно!
Варианты индивидуальных заданий:
| Вар. | Задание: | Вар. | Задание: |
| 1. | A =(1,3,6), B =(2,2,1), C =(-1,0,1), D =(-4,6,3). | 16. | A =(1,5,-7), B =(-3,6,3), C =(-2,7,3), D =(-4,8,-12). |
| 2. | A =(-4,2,6), B =(2,-3,0), C =(-10,5,8), D =(-5,2,4). | 17. | A =(-3,4,-7), B =(1,5,-4), C =(-5,-2,0), D =(2,5,4). |
| 3. | A =(7,4,2), B =(7,-1,-2), C =(3,3,1), D =(-4,2,1). | 18. | A =(-1,2,-3), B =(4,-1,0), C =(2,1,-2), D =(3,4,5). |
| 4. | A =(2,1,4), B =(-1,5,-2), C =(-7,3,2), D =(-6,-3,6). | 19. | A =(4,-1,3), B =(-2,1,0), C =(0,-5,1), D =(3,2,-6). |
| 5. | A =(-1,-5,2), B =(-6,0,3), C =(3,6,-3), D =(-10,6,7). | 20. | A =(1,-1,1) B =(-2,0,3), C =(2,1,-1), D =(2,-2,4). |
| 6. | A =(0,-1,-1), B =(-2,3,5), C =(1,5,-9), D =(-1,-6,3). | 21. | A =(1,2,0), B =(1,-1,2), C =(0,1,-1), D =(-3,0,1). |
| 7. | A =(5,2,0), B =(2,5,0), C =(1,2,4), D =(-1,1,1). | 22. | A =(1,0,2), B =(1,2,-1), C =(2,-2,1), D =(2,1,0). |
| 8. | A =(2,-1,-2), B =(1,2,1), C =(5,0,-6), D =(-10,9,-7). | 23. | A =(1,2,-3), B =(1,0,1), C =(-2,-1,6), D =(0,-5,-4). |
| 9. | A =(-2,0,-4), B =(-1,7,1), C =(4,-8,-4), D =(1,-4,6). | 24. | A =(3,10,-1), B =(-2,3,-5), C =(-6,0,-3), D =(1,-1,2). |
| 10. | A =(4,4,5), B =(-5,-3,2), C =(-2,-6,-3), D =(-2,2,-1). | 25. | A =(-1,2,4), B =(-1,-2,-4), C =(3,0,-1), D =(7,-3,1). |
| 11. | A =(1,2,0), B =(3,0,-3), C =(5,2,6), D =(8,4,-9). | 26. | A =(0,-3,1), B =(-4,1,2), C =(2,-1,5), D =(3,1,-4). |
| 12. | A =(2,-1,2), B =(1,2,-1), C =(3,2,1), D =(-4,2,5). | 27. | A =(-1,0,3), B =(4,2,1), C =(-3,-1,0), D =(4,1,5). |
| 13. | A =(1,1,2), B =(-1,1,3), C =(2,-2,4), D =(-1,0,-2). | 28. | A =(2,4,-2), B =(0,1,-3), C =(1,4,7), D =(-3,0,5). |
| 14. | A =(2,3,1), B =(4,1,-2), C =(6,3,7), D =(7,5,-3). | 29. | A =(-1,0,2), B =(3,7,1), C =(1,2,5), D =(-4,0,1). |
| 15. | A =(1,1,-1), B =(2,3,1), C =(3,2,1), D =(5,9,-8). | 30. | A =(2,3,4), B =(-5,1,0), C =(2,7,1), D =(-3,0,5). |
Прямая на плоскости.
2.1. Даны уравнения двух прямых. Составить уравнение биссектрисы тупого угла, образованного этими прямыми.
Общие сведения и расчётные формулы: по представленному заданию.
Пусть имеем две прямые: 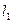 :
: 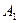 x +
x + 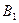 y +
y + 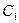 = 0 и
= 0 и 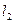 :
: 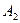 x +
x + 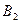 y +
y + 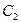 = 0. Уравнением
= 0. Уравнением 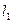 определяется вектор нормали
определяется вектор нормали 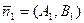 , уравнением
, уравнением 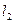 вектор нормали
вектор нормали 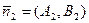 . Так как векторы
. Так как векторы 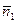 и
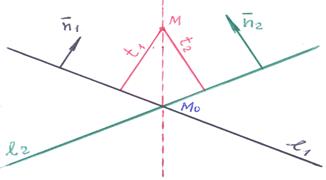
и 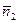 – свободные, то изобразим их так, чтобы их начала принадлежали соответствующим плоскостям, а сами они располагались внутри одного из углов, образованных пересекающимися прямыми. Важно помнить также, что уравнение прямой можно умножать на произвольное, не равное нулю число. Это значит, что, по необходимости, мы можем разместить векторы
– свободные, то изобразим их так, чтобы их начала принадлежали соответствующим плоскостям, а сами они располагались внутри одного из углов, образованных пересекающимися прямыми. Важно помнить также, что уравнение прямой можно умножать на произвольное, не равное нулю число. Это значит, что, по необходимости, мы можем разместить векторы 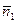 и
и 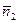 как внутри тупого, так и внутри острого угла. Пусть векторы
как внутри тупого, так и внутри острого угла. Пусть векторы 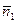 и
и 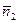 разместились внутри тупого угла, как показано на рисунке. Умножим уравнение
разместились внутри тупого угла, как показано на рисунке. Умножим уравнение 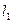 на число (-1). Вектор нормали этой прямой станет равным
на число (-1). Вектор нормали этой прямой станет равным 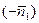 , и пара векторов
, и пара векторов 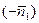 и
и 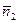 расположится внутри острого угла. Видим, когда векторы нормалей плоскостей располагаются внутри тупого угла угол между ними острый. И наоборот, если векторы расположились внутри острого угла, то угол между ними тупой. Какой из случаев реализуется в конкретном примере, легко определить при помощи скалярного произведения:
расположится внутри острого угла. Видим, когда векторы нормалей плоскостей располагаются внутри тупого угла угол между ними острый. И наоборот, если векторы расположились внутри острого угла, то угол между ними тупой. Какой из случаев реализуется в конкретном примере, легко определить при помощи скалярного произведения:
а) 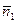 ∙
∙ 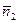 > 0 – векторы расположены в области тупого угла;
> 0 – векторы расположены в области тупого угла;
б) 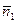 ∙
∙ 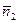 < 0 – векторы расположены в области острого угла.
< 0 – векторы расположены в области острого угла.
Так как от случая а) легко перейти к случаю б), то для определённости будем считать, что всегда нужно строить биссектрису тупого угла.
 Отметим факт: рассматриваемую задачу относят к классическим задачам аналитической геометрии. Важно также то, что существует несколько способов решения этой задачи, причём существенно различающихся как по теоретическим основам, так и технологии применяемых вычислений!
Отметим факт: рассматриваемую задачу относят к классическим задачам аналитической геометрии. Важно также то, что существует несколько способов решения этой задачи, причём существенно различающихся как по теоретическим основам, так и технологии применяемых вычислений!
Способ– 1. Пусть 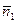 ∙
∙ 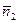 > 0: векторы
> 0: векторы 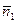 и
и 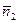 располагаются в области тупого угла.
располагаются в области тупого угла.
Воспользуемся свойством биссектрисы: каждая принадлежащая ей точка одинаково удалена от сторон угла, который биссектриса делит пополам.
Для эффективного (и удобного) использования понятия расстояние от точки до прямой, каждое из уравнений заданных прямых необходимо нормализовать. Нормированное уравнение прямой удобно как для вычисления откло