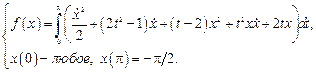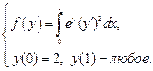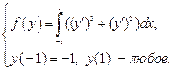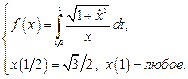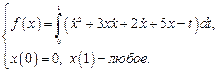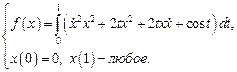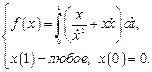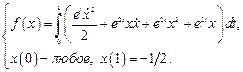Пусть даны две точки  ,
,  плоскости
плоскости  , пусть
, пусть  . Пусть далее
. Пусть далее  – уравнение кривой, соединяющей точки
– уравнение кривой, соединяющей точки 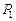 и
и  , т.е.
, т.е.  ,
,  . Кривая вращается вокруг оси
. Кривая вращается вокруг оси  , заметая некоторую поверхность вращения. Спрашивается, что представляет собой поверхность вращения, имеющая наименьшую возможную площадь. Таким образом, мы приходим к проблеме выбора функции
, заметая некоторую поверхность вращения. Спрашивается, что представляет собой поверхность вращения, имеющая наименьшую возможную площадь. Таким образом, мы приходим к проблеме выбора функции  , для которой интеграл
, для которой интеграл

– площадь поверхности вращения – минимален. Такие минимальные поверхности вращения, при некоторых дополнительных ограничениях на точки 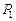 и
и  , называются катеноидами.
, называются катеноидами.
Функция F в этом случае имеет вид 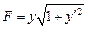 , то есть не зависит от x. Первый интеграл дается равенством
, то есть не зависит от x. Первый интеграл дается равенством
 , и тогда
, и тогда  .
.
Решая это уравнение в разделяющихся переменных, получаем
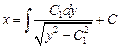 .
.
Удобно далее положить  . Тогда
. Тогда
 .
.
Положим  и
и  , тогда окончательно
, тогда окончательно  – искомая кривая (цепная линия).
– искомая кривая (цепная линия).
Список рекомендуемой литературы
1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление / Л.Э. Эльсгольц. – М.: Эдиториал УРСС, 2000. – 319 с.
2. Романко В.К. Курс дифференциальных уравнений и вариационного исчисления / В.К. Романко. – М., СПб.: Физматлит, 2000. – 342 с.
3. Пантелеев А.В. Вариационное исчисление в примерах и задачах / А.В. Пантелеев. – М.: Изд-во МАИ, 2000. – 227 с.
Варианты заданий
Задание 5
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе.
1.  ,
,
 – сектор круга:
– сектор круга:  .
.
Граничные условия: 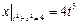 ,
, 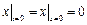 .
.
2.  ,
,
 – кольцо:
– кольцо:  .
.
Граничные условия:  ,
,  .
.
3.  ,
,
 – круг:
– круг:  .
.
Граничные условия:  .
.
4.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 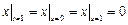 ,
,  .
.
5.  ,
,
 – сектор кольца:
– сектор кольца:  .
.
Граничные условия:  ,
, 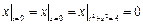 .
.
6.  ,
,
 – сектор круга:
– сектор круга: 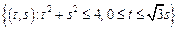 .
.
Граничные условия:  ,
,  .
.
7.  ,
,
 – кольцо:
– кольцо:  .
.
Граничные условия:  ,
, 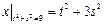 .
.
8.  ,
,
 – круг:
– круг:  .
.
Граничные условия:  .
.
9.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия:  ,
, 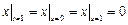 .
.
10.  ,
,
 – сектор кольца:
– сектор кольца:  .
.
Граничные условия:  ,
, 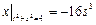 .
.
11.  ,
,
 – сектор круга:
– сектор круга:  .
.
Граничные условия:  ,
, 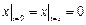 .
.
12.  ,
,
 – кольцо:
– кольцо:  .
.
Граничные условия: 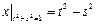 ,
,  .
.
13.  ,
,
 – круг:
– круг:  .
.
Граничные условия:  .
.
14.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия:  ,
,  ,
,  .
.
15.  ,
,
 – сектор кольца:
– сектор кольца:  .
.
Граничные условия:  ,
, 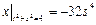 .
.
16.  ,
,
 – сектор круга:
– сектор круга:  .
.
Граничные условия: 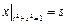 ,
,  .
.
17.  ,
,
 – кольцо:
– кольцо:  .
.
Граничные условия:  ,
,  .
.
18.  ,
,
 – круг:
– круг:  .
.
Граничные условия: 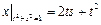 .
.
19.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия:  ,
,  ,
,  .
.
20.  ,
,
 – сектор кольца:
– сектор кольца:  .
.
Граничные условия:  ,
,  .
.
21.  ,
,
 – сектор круга:
– сектор круга:  .
.
Граничные условия:  ,
, 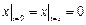 .
.
22.  ,
,
 – кольцо:
– кольцо:  .
.
Граничные условия:  ,
,  .
.
23.  ,
,
 – круг:
– круг:  .
.
Граничные условия: 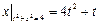 .
.
24.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия:  ,
,  ,
, 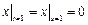 .
.
25.  ,
,
 – сектор кольца:
– сектор кольца: 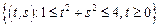 .
.
Граничные условия:  ,
,  .
.
26.  ,
,
 – сектор круга:
– сектор круга:  ,
, 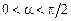 .
.
Граничные условия:  ,
,  , где
, где  – произвольная непрерывная на отрезке
– произвольная непрерывная на отрезке  функция.
функция.
27.  ,
,
 – кольцо:
– кольцо:  .
.
Граничные условия:  ,
,  .
.
28.  ,
,
 – круг:
– круг:  .
.
Граничные условия:  .
.
29.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 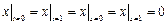 .
.
30.  ,
,
 – сектор кольца:
– сектор кольца: 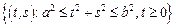 ,
,  – непрерывная на отрезке
– непрерывная на отрезке 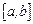 функция.
функция.
Граничные условия:  .
.
Задание 6
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе, используя для построения решения функции Бесселя и многочлены Лежандра.
1.  ,
,
 – прямой круговой цилиндр:
– прямой круговой цилиндр: 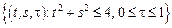 .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
2.  ,
,
 – прямой круговой цилиндр:
– прямой круговой цилиндр:  .
.
Граничные условия: 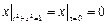 ,
, 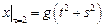 , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
3.  ,
,
 – прямой круговой цилиндр:
– прямой круговой цилиндр:  .
.
Граничные условия: 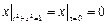 ,
, 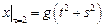 , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
4.  ,
,
 – шар:
– шар:  .
.
Граничные условия:  .
.
5.  ,
,
 – шар:
– шар: 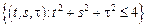 .
.
Граничные условия: 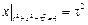 .
.
6.  ,
,
 – шар:
– шар:  .
.
Граничные условия:  .
.
7.  ,
,
 – шар:
– шар:  .
.
Граничные условия: 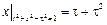 .
.
8.  ,
,
 – шар:
– шар: 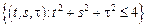 .
.
Граничные условия:  .
.
9.  ,
,
 – круг:
– круг:  .
.
Граничные условия: 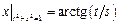 .
.
10.  ,
,
 – сектор круга:
– сектор круга:  .
.
Граничные условия: 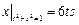 ,
, 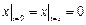 .
.
11.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 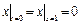 ,
,  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
12.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 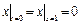 ,
,  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
13.  ,
,
 – прямоугольник:
– прямоугольник:  .
.
Граничные условия:  ,
,  ,
, 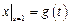 ,
,
где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
14.  ,
,
 – прямоугольник:
– прямоугольник:  .
.
Граничные условия:  ,
,  ,
, 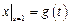 ,
,
где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
15.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 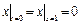 ,
,  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
16. 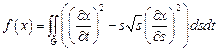 ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 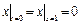 ,
,  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
17.  ,
,
 – прямоугольник:
– прямоугольник:  .
.
Граничные условия:  ,
,  ,
, 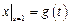 ,
,
где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
18. 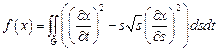 ,
,
 – прямоугольник:
– прямоугольник:  .
.
Граничные условия:  ,
,  ,
, 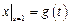 ,
,
где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
19.  ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 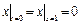 ,
,  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
20. 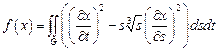 ,
,
 – квадрат:
– квадрат:  .
.
Граничные условия: 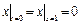 ,
,  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
21.  ,
,
 – прямоугольник:
– прямоугольник:  .
.
Граничные условия:  ,
,  ,
, 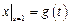 ,
,
где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
22. 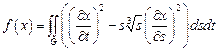 ,
,
 – прямоугольник:
– прямоугольник:  .
.
Граничные условия:  ,
,  ,
, 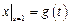 ,
,
где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
23.  ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
24.  ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
25.  ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия: 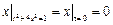 ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
26.  ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия: 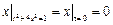 ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
27. 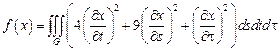 ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
28. 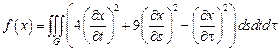 ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке  функция.
функция.
29. 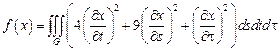 ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке 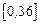 функция.
функция.
30. 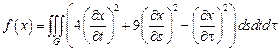 ,
,
 – эллиптический цилиндр:
– эллиптический цилиндр:  .
.
Граничные условия:  ,
,  , где
, где  – непрерывная на отрезке
– непрерывная на отрезке 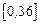 функция.
функция.
Задание 7
Решить задачу навигации при условии, что собственная скорость лодки постоянна, а скорость реки задается указанным ниже равенством. Предполагая, что  , построить график движения лодки, при котором переправа осуществится за минимальное время.
, построить график движения лодки, при котором переправа осуществится за минимальное время.
-

-

-
 .
. -
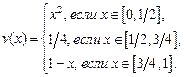
-

-

-
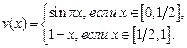
-

-

-
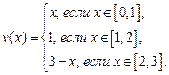
-

-

-

-
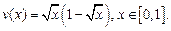
-

-

-

-

-

-

-

-
 .
. -
 .
. -
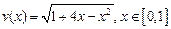 .
. -
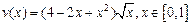 .
. -

-

-

-

-

Задание 8
Найти экстремали следующих вариационных задач с подвижными границами.
Задание 9
Найти решение следующих изопериметрических задач.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
14. 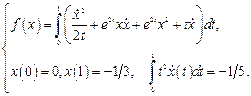
19. 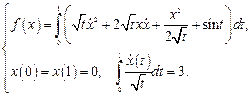
23. 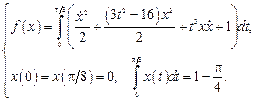
Задание 10
Сформулировать следующие задачи как задачи на отыскание экстремумов некоторых интегральных функционалов и решить их методами вариационного исчисления.
- Найти замкнутую линию наименьшей длины, ограничивающую заданную площадь S.
- Найти замкнутую линию заданной длины L, ограничивающую наибольшую площадь.
- Даны два взаимно перпендикулярных луча ОА и ОВ с общей вершиной О. Среди кривых заданной длины L, концы которых лежат на ОА и ОВ, найти такую, которая отсекает от угла АОВ максимальную площадь.
- Даны два взаимно перпендикулярных луча ОА и ОВ с общей вершиной О. Среди кривых с концами на ОА и ОВ, отсекающих от угла АОВ заданную площадь S, найти кривую наименьшей длины.
- В равностороннем треугольнике провести кривую заданной длины, которая образовала бы вместе с углом треугольника фигуру наибольшей площади.
- В равностороннем треугольнике провести кривую наименьшей длины, которая образовала бы вместе с углом треугольника фигуру заданной площади.
- Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 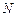 , со скоростью, прямо пропорциональной абсциссе точки в каждый момент времени. Найти кривую
, со скоростью, прямо пропорциональной абсциссе точки в каждый момент времени. Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую
со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую  , соединяющую начало координат с точкой на прямой
, соединяющую начало координат с точкой на прямой  , и такую, что время движения вдоль нее будет минимальным.
, и такую, что время движения вдоль нее будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую
со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую  , соединяющую начало координат с точкой на прямой
, соединяющую начало координат с точкой на прямой 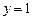 , и такую, что время движения вдоль нее будет минимальным.
, и такую, что время движения вдоль нее будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую
со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую  , соединяющую начало координат с точкой на прямой
, соединяющую начало координат с точкой на прямой  , и такую, что время движения вдоль нее будет минимальным.
, и такую, что время движения вдоль нее будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую
со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую  , соединяющую начало координат с точкой на окружности
, соединяющую начало координат с точкой на окружности  , и такую, что время движения вдоль нее будет минимальным.
, и такую, что время движения вдоль нее будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 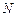 , со скоростью, обратно пропорциональной абсциссе точки в каждый момент времени. Найти кривую
, со скоростью, обратно пропорциональной абсциссе точки в каждый момент времени. Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 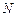 , со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую
, со скоростью, прямо пропорциональной ординате точки в каждый момент времени. Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 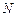 , со скоростью, обратно пропорциональной ординате точки в каждый момент времени. Найти кривую
, со скоростью, обратно пропорциональной ординате точки в каждый момент времени. Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 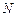 , со скоростью
, со скоростью  (k – постоянный коэффициент). Найти кривую
(k – постоянный коэффициент). Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 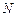 , со скоростью,
, со скоростью,  (k – постоянный коэффициент). Найти кривую
(k – постоянный коэффициент). Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 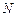 , со скоростью,
, со скоростью,  (k – постоянный коэффициент). Найти кривую
(k – постоянный коэффициент). Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Материальная точка перемещается вдоль плоской кривой
 , соединяющей точки
, соединяющей точки  и
и 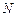 , со скоростью,
, со скоростью,  (k – постоянный коэффициент). Найти кривую
(k – постоянный коэффициент). Найти кривую  , время движения вдоль которой из точки М в точку N будет минимальным.
, время движения вдоль которой из точки М в точку N будет минимальным. - Решить задачу о брахистохроне, если известно, что шарик должен оказаться на некоторой вертикальной прямой.
- Решить задач