Вариационными задачами на условный экстремум называются задачи, в которых экстремум функционала находится в предположении, что на функции, от которых зависит функционал, накладываются некоторые дополнительные условия (связи).
Например, пусть ищется экстремум функционала
(12)
при наличии условий
. (13)
Наиболее естественный путь заключается в разрешении системы (13), уравнения которой считаем независимыми, относительно каких-нибудь 
переменных – например, относительно 
– и подстановки найденных переменных в (12). При этом функционал 
будет зависеть уже от 
переменных 
, которые уже независимы, и следовательно, задача свелась к исследованию функционала 
на безусловный экстремум. К этой задаче применимы методы, изложенные в предыдущих разделах.
Легко, однако, заметить, что этот метод срабатывает далеко не всегда, поскольку задача явно выразить переменные через остальные может оказаться очень трудной (если вообще разрешимой). Поэтому для решения вариационных задач на условный экстремум чаще применяют метод, известный как метод множителей Лагранжа.
Этот метод состоит в построении вспомогательной функции
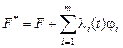, (14)
в терминах которой и формулируется решение задачи на условный экстремум.
Теорема. Пусть функции реализуют экстремум функционала (12) при условиях связи (13). Тогда функции являются решением системы уравнений вида:
(15)
Таким образом, для решения задачи на условный экстремум следует:
- Составить вспомогательную функцию
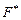по формуле (14). - Записать и решить для нее систему уравнений Эйлера, дополненную условиями связи (15).
- Найти произвольные постоянные из граничных условий (они могут быть любого вида, как жестко закрепленные, так и подвижные).
В процессе реализации этой программы, как правило, находятся еще и вспомогательные функции 
, которые не обязательны для построения решения, но могут оказаться полезными при решении системы (15).
Пример 8. Найти экстремум функционала
,
если переменные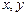 
подчинены условию связи 
и удовлетворяют граничным условиям: 
.
Решение. Составим вспомогательную функцию по формуле (14):
.
Система уравнений Эйлера для функции 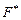имеет вид:
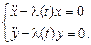
Для этой системы нет общего метода решения, так как функция 
зависит от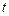 
, а вид ее неизвестен. Поэтому попытаемся получить дополнительную информацию о функциях 
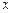и 
из условия связи. Так как 
, то из условия связи следует, что 
, то есть 
. Следовательно, переменную 
можно заменить на 
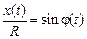, то есть 
, а тогда 
. Переходя к новым переменным, приводим систему уравнений Эйлера к виду:
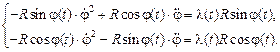
Домножая первое уравнение на 
, а второе на 
и вычитая из первого уравнения второе, получаем: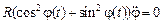 
, откуда следует, что 
, то есть 
, а функци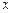и и имеют вид: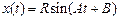 
, 
. Из граничных условий получаем: 
, следовательно, 
или 
; 
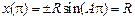, следовательно, 
, где 
– целое число. Подставляя найденные постоянные в выражение для 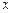и , получаем бесконечное множество экстремалей:
, 
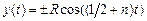, где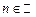 
.