В качестве иллюстрации построенной теории решим три классические задачи: задачу Дидоны, задачу о брахистохроне и задачу о минимальной поверхности вращения. Каждую из этих задач сначала переформулируем в вариационных терминах, то есть поставим ее как задачу отыскания минимума функционала с заданными граничными условиями, а затем решим ее разработанными выше методами вариационного исчисления.
Задача Дидоны
Вспомним задачу, о которой говорилось в начале курса: мы оставили Дидону в тот момент, когда ей нужно было ограничить шнуром фиксированной длины максимальную площадь. Мы уже освоили вариационное исчисление настолько хорошо, что можем помочь Дидоне.
Рассмотрим множество функций 
, определенных на отрезке 
, таких, что 
при всех 
, а 
(рис. 3). Вместе с отрезком график каждой функции 
ограничивает площадь, задаваемую функционалом
.
Потребуем дополнительно, чтобы кривые имели фиксированную длину, то есть постоянное значение сохранял функционал вида:
.
Мы получаем, таким образом, изопериметрическую задачу, для которой нам уже известны методы решения.
Выстраиваем вспомогательную функцию 
и записываем для нее уравнение Эйлера. Функция 
не зависит от переменной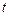 
, следовательно, уравнение Эйлера допускает первый интеграл
,
представляющий собой дифференциальное уравнение первого порядка, не разрешенное относительно производной. Разрешая его относительно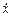 
, получаем уравнение в разделяющихся переменных, интегральными кривыми которого являются окружности:
.
Учитывая граничные условия, находим, что 
, а 
. Не нарушая общности, можем считать, что интересующая нас дуга окружности не больше ее половины, тогда центр окружности лежит ниже оси 
, и 
. Для определения параметра 
, то есть радиуса искомой окружности, используем условие постоянства периметра.
|
|
.
Уравнение 
эквивалентно уравнению 
где 
, 
, 
. Из геометрических соображений ясно, что задача содержательна лишь при условии 
, следовательно, 
, а тогда уравнение 
всегда имеет на отрезке 
единственный корень 
(рис. 4).
Отсюда находим радиус искомой окружности 
и координаты ее центра: 
.
Задача о брахистохроне
Предположим, что точки 
и 
лежат в плоскости 
с осью 
, направленной вниз (рис.5). Положим 
и 
и пусть 
– уравнение дуги, соединяющей точки и так, что 
, 
, 
, 
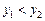. Скорость движения вдоль кривой пусть равна 
. Тогда время спуска равно
.
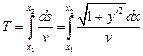Чтобы найти скорость v как функцию координаты x, воспользуемся законом сохранения энергии:
,
где 
— начальная скорость движения частицы. Тогда
,
и задача свелась к выбору функции 
, для которой интеграл
достигает наименьшего значения из всех возможных.
Так как функция 
зависит только от 
и 
, то уравнение Эйлера допускает первый интеграл:
.
Разрешая это уравнение относительно , находим
,
где мы положили 
. Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем:
.
Для вычисления интеграла удобно воспользоваться заменой
. Тогда 
.
Мы пришли к решению в параметрической форме
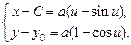
Это и есть кривая наибыстрейшего спуска, известная под названием циклоиды. Можно показать, что выбор постоянных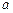 
и 
позволяет провести циклоиду через произвольные две заданные точки. Напомним, что величина 
не является произвольной постоянной.