А.С.Харитонов
АННОТАЦИЯ
В работе рассматривается возникновение пространства как результат взаимодействия бытия и небытия, описываемых осцилляцией процессов рассеяния и концентрации энергии с помощью мер хаоса и порядка в трех классах переменных для целостных систем с переменной внутренней организацией. Работа является продолжением и развитием статей, опубликованных в предыдущих сборниках Казначеевские чтения 2009г. №1, 2.
Исходные логико-онтологические постулаты структурируют наше мышление и определяют те закономерности природы, которые мы познаем, и которые определяют цель и смысл нашего существования. Исходные логико-онтологические постулаты, в том числе математики, могут быть разными и приводить к разным картинам мира, то есть приводить к неумышленным заблуждениям.
С одной стороны известно, что в каждой науке столько истины, сколько в ней математики, а с другой стороны, если принятые исходные математические аксиомы, постулаты и гипотезы исключают из рассмотрения исследуемые свойства природы, то такая математика является дополнительным источником заблуждений. На целесообразность проверять соответствие исходных математических аксиом теории целям описания объектов природы обращал внимание еще Л.Больцман. Действительно, на одних исходных постулатах наука описала эволюцию природы к максимальному хаосу согласно статистическому выражению второго закона термодинамики, а на других исходных началах наука еще ранее описала эволюцию природы к гармонии, которая получила математическое выражение в трудах Л.Пачоли, Л.да Винчи. И.Кеплера, Г.Лейбница, Ш.Фурье.
И.Ньютон оговорил постулаты и гипотезы, при которых можно пренебрегать эволюцией и самодвижением природы, и описывать часть явлений природы обратимыми во времени уравнениями механики, постулируя существование пространства, времени и вещества и постоянство их свойств.
|
|
Дальнейшее бурное развитие науки пошло на постулатах и гипотезах механики Ньютона, что привело к забвению законов эволюции природы к гармонии, которые порождают наши представления о пространстве, веществе и движении. Забвение законов эволюции к гармонии породило рост социальных кризисов и научных противоречий в понимании феноменов эволюции и развития природы. Так существование природы, и особенно биологических и социальных систем, связано с концентрацией энергии, и научно-технический прогресс определяется совершенствованием процесса концентрации энергии. А постулаты механики И.Ньютона исключают рассмотрение эволюции и феномена концентрации энергии. Поэтому теории, использующие исходные постулаты механики И.Ньютона, термодинамика, статистическая механика, квантовая механика и релятивистская механика не описывают эволюции и процесса концентрации энергии в природе, и поэтому этих наук недостаточно для познания научной сущности эволюции и развития природы, человека и общества.
Закон эволюции предшествует условиям развитии природы и общества, а вместе законы эволюции и развития определяют разумную цель и стратегию социального управления. Сегодня игнорирование закономерностей эволюции, развития и концентрации энергии привело цивилизацию к росту социальных кризисов, техногенных аварий и угрозе экологической и демографической катастрофы.
|
|
Поэтому автор исследует в своих работах новые исходные аксиомы математики, которые позволят описать эволюцию, развитие и процесс концентрации энергии в природе.
Математика развивалась преимущественно из практических нужд при описании наблюдаемых свойств объектов природы от простого к сложному. Сталкиваясь с новыми свойствами объектов природы, в математику вводили новые постулаты, которые лучше согласуются с опытом для описания все более сложных природных закономерностей. В результате построено здание науки в виде теорий, построенных на общих исходных аксиомах о пространстве и своих специальных гипотезах. При этом недостаток и ограничения одних аксиом и постулатов часто компенсируются введением дополнительных гипотез, которые компенсируют друг друга для некоторых прикладных целей исследования. Однако такое развитие математики породило в науке неразрешенные парадоксы «тепловой смерти Вселенной», «возникновения порядка из хаоса», «Бог играет в кости», невозможность отличить живое тело от мертвого и новую гипотезу о «Большом взрыве Вселенной».
В работах автора были выделены аксиомы, которые исключили из научного рассмотрения описание эволюции и процесса концентрации энергии в природе. К этим аксиомам автор отнес в первую очередь свойства натурального ряда чисел, где число А и его порядковый номер n совпадают: A(n)=n, аксиомы геометрии, позволяющие рассматривать только повторяющиеся закономерности природы, постулаты И.Ньютона о возможности рассматривать системы и силы, приводящих к изменению их состояния, по отдельности, то есть материю в виде бесструктурного вещества в пространстве и причину ее движения по отдельности, а также постулат Л.Больцмана о равновероятности допустимых микросостояний в статистической механике. Постулат Л.Больцмана исключает рассмотрение процесса концентрации энергии и совпадает с постулатом Дж.Гиббса о микроканоническом распределении энергии, справедливость которого Дж.Гиббс ограничил рассмотрением только консервативных систем, когда эволюцией можно пренебречь.
|
|
Механика и ее постулаты послужили основой для философии диалектического материализма, которая определила по-своему общие законы развития природы и общества. Эта философия ввела антагонистические силы и классовую борьбу в обществе по аналогии с силами в механике и термодинамике и сделала вывод о поступательном развитии общества к некоторому конечному состоянию – коммунизму. Такой вывод не соответствует практике современного общества и современным знаниям об эволюции и развитии сложных систем. В действительности социальные системы, обладая самодвижением, самоорганизацией в иерархические структуры и «вечной борьбой сил», описываются иными общими законами развития природы. Управление обществом на основе диалектического материализма и представления, что материя движется только в пространстве и времени, приводит к саморазрушению согласно второму закону термодинамики, как это еще предвидел Н.Макиавелли для государства противника.
Для выживания и развития человечество должно научиться управлять процессами рассеяния и концентрации энергии, которые не познаваемы на основе современной физики. Поясним это важное обстоятельство.
Эволюция замкнутых систем описывается с помощью натурального ряда чисел, геометрии Евклида и на законах механики И.Ньютона как стремление к максимальному хаосу согласно статистическому выражению второго закона термодинамики, предложенного Л.Больцманом в 1878 году. Эволюция же выживающих систем описывается стремлением к гармонии по формуле «божественной или золотой» пропорции, как это впервые показали еще Л.Пачоли и Л.да Винчи в 1509 году на основе других исходных постулатов. Н.Макиавелли предложил в 1514 году скрывать законы эволюции к гармонии для государства противника с целью его саморазрушения. Законы эволюции и развития определяют разумную стратегическую цель действий человека и социального управления. Сегодня в глобализирующимся мире социальное управление без собственной математической базы увеличило рост числа кризисов, социальных катастроф и техногенных аварий и представляет угрозу всему обществу. Поэтому определяющие значение для современного социального управления играют объективные знания о глубине понимания закономерностей эволюции и развития природы, человека и общества, а, следовательно, выбор исходных аксиом и постулатов математического описания природы играет определяющую роль в жизни современного общества.
Так постулаты и законы И.Ньютона позволяют рассматривать механические системы и силы, приводящие к изменению их состояния, по отдельности, так чтобы любое изменение состояния частицы (центра тяжести тела) можно было рассматривать, как результат внешнего воздействия детерминированной силы на основе закона тождества:
А≡А (1)
в математической логике, закона инерции Г.Галилея, и в соответствии с воспроизводимыми экспериментами во внешней инвариантной системе отсчета.
Механика И.Ньютона описывает только обратимые во времени динамические процессы под действием внешних сил, когда всем, что возникает и исчезает, можно пренебречь, и не учитывает целостность природы, откуда и как возникают силы в природе. То есть механика пренебрегает феноменом самодвижения природы, приводящим к изменению организации систем.
Внешняя сила всегда ослабевает в системах согласно известному опыту, и поэтому эволюция механических систем описывается стремлением к равновесию сил действия противодействия (третий закон Ньютона). На основе постулатов и законов механики И.Ньютона термодинамика, пренебрегая природой вещества, описывает эволюцию систем к «тепловой смерти Вселенной», а статистическая механика описывает эволюцию замкнутых систем к максимальному хаосу по постулату Л.Больцмана. Такие описание эволюции природы противоречит самому факту существования природы, концентрации энергии в известных формах вещества, «вечной борьбе сил» в природе и, в конечном итоге, существованию самого человека. В поиске разрешения противоречий «тепловой смерти Вселенной», «возникновения порядка из хаоса», «Бог не играет в кости» в ХХ веке возникла гипотеза «Большого взрыва Вселенной», и в современной синергетике принято рассматривать развитие только в открытых неравновесных системах, нарушая целостность научной картины мира. В тоже время известно /А.Фридман, И.Лифшиц, Л.Шелепин, А.Харитонов/, что сложные физические системы, в которых определяющую роль играют распределенные параметры, например, переменная плотность вещества, внутренняя память и переменная структура динамических элементов, не приемлемо рассмотрение систем и ее движущих сил по отдельности. Другими словами, пренебрегать целостностью природы, феноменом ее самодвижения и процессом концентрации энергии в общем случае нельзя. Тем более отдельное рассмотрение системы и ее движущих сил не приемлемо для описания биологических и социальных систем, где переменная структура динамических элементов и человека, в частности, способна приводить к самодвижению, разрушению и развитию общества даже при постоянстве внешних условий. Н.А.Умов предложил в 1902 году для описания биологических систем добавить к механическим и термодинамическим переменным структуру динамических элементов. Резонансы взаимодействия структуры динамических элементов позволяют представить возникновение внутренних движущих сил в системе, за счет которых биологические системы работают против второго закона термодинамики и находятся периодически в состоянии самодвижения и стремятся поддерживать свою целостность. М.Планк отметил, что если химические структурные превращения вещества и механическое движение частиц влияют друг на друга, и нельзя рассматривать суперпозицию этих процессов, то законы статистической механики становятся не приемлемыми для описания таких сложных систем. Поэтому для описания эволюции и самодвижения сложных физических, биологических и социальных систем необходим поиск альтернативных способов описания природы на других исходных постулатах математики, где система целостна и ее движущие силы находятся внутри нее.
Физика И.Ньютона сформировалась как альтернатива метафизике Аристотеля, в которой описание природы рассматривается от единого и целого, как взаимодействие бытия и небытия, порождая становление природы, в которой выживающие системы стремятся к тройственной гармонии. К метафизике Аристотеля автор относит: последовательность чисел Фибоначчи /1202/, «Божественную пропорцию» Лука Пачоли и Леонардо да Винчи /1509/, модель Солнечной системы в «Гармонии мира» И.Кеплера /1619/, «Предустановленную гармонию» Г.Лейбница/1695/, «Всемирную гармонию» Ш.Фурье/1803/, а так же работы по математическому описанию гармонии в архитектуре, музыке и живописи. Описание эволюции к гармонии построено на уравнении рекурсии:
Аn= Аn-1 + Аn-2. (2)
Эта рекурсия содержит закон тождества, на котором построена механистическая картина мира, как свой частный случай при Аn-2 =0.
Сегодня социология и экономика используют математику описания эволюции к гармонии в методе Фибоначчи, однако, без его теоретического обоснования /А. Эрлих/.
Итак, есть два начала выбора аксиом и постулатов математики.
1) На основании наблюдаемых свойств природы, подтверждаемых в повторяемых опытах, к исследованию от простых к более сложным свойствам природы с помощью натурального ряда чисел, удовлетворяющих закону тождества А≡А, аксиом геометрии, гипотезы об эквивалентности алгебры и геометрии, введения внешней инерциальной система отсчета и постулируя существование однородного и изотропного пространства и времени.
2) На основании гипотезы о единстве и целостности природы, которое предполагает такое разбиение целого на оптимальные части, которое совместимо с известным опытом и рекуррентным уравнением (2), описывающим эволюцию природы к гармонии..
Закон тожества (1) противоречит феномену эволюции, отмеченного еще афоризмом Гераклита: «Дважды нельзя войти в одну реку».
Машины производят полезную работу в пространстве и времени при постоянстве структуры динамических элементов за счет внешних источников энергии, что удовлетворяет моделям, построенным на законе тождества (1) для выбранных наблюдаемых параметров рассматриваемых систем. Организмы же функционируют и живут главным образом за счет изменения структуры, составляющих его элементов, формируя неоднородное пространства, нарушая закон тождества для сохранения единства и целостности природы.
Описание физических систем на основе закона тождества построено на модели равновесия материальной точки /Г.Галилей/ в однородном и изотропном пространстве и времени во внешней инерциальной системе отсчета. Развитие физики на таких началах привело к представлению о мире как открытой неравновесной системе, подверженной внешней сверхъестественной силе, то есть к нарушению единства и целостности природы.
Первый вариант выбора аксиом математики позволил описать эволюцию систем, пренебрегая структурой вещества, как стремление к максимальному хаосу согласно статистическому выражению второго закона термодинамики, а второй вариант показал, хотя и слабо математически разработан, что эволюция природы стремится к гармонии структур, описываемой золотой пропорцией.
Поэтому давно существует практическая и теоретическая необходимость поиска новых исходных постулатов математики, которые должны включать в себя как физику Ньютона, так и метафизику Аристотеля, а также законы диалектического материализма как свои частные случаи.
Автор предложил в 1971 году новый способ описания качества систем с помощью новых математических функций мер хаоса и порядка, где мера порядка описывает процесс концентрации энергии. В 1978 году автор предложил новый постулат о равновесии в среднем мер хаоса и порядка для статистического описания систем от равновесия целого к исследованию эволюции его частей. В 1990 году автор защитил кандидатскую диссертацию по теоретической физике по описанию статистического равновесия сложных систем с переменной структурой динамических элементов на примере макромолекулы и описал на ее примере статистические закономерности развитии физических систем в трех классах переменных. Эти исследования автора позволили высказать предположение, что разным исходным постулатам математики от простого к сложному и от целого к эволюции его частей соответствуют две разные физики.
1) Одна физика консервативных или эргодических систем основана на экспериментах, когда систему и действующие на нее силы можно рассматривать раздельно, постулируя молчаливо множество рабочих гипотез, например, о свойствах пространства, времени, частиц и взаимодействия между ними, строя математическое описание систем во внешней инерциальной системе отсчета;
2) Другая физика – метафизика становления бытия строится на основании гипотезы о единстве и целостности природы с помощью постулата о равенстве мер хаоса и порядка в трех классах переменных.
Первый вариант физики консервативных систем достиг своего апогея, но противоречит опыту эволюции и развития систем, а второй вариант физики – метафизики становления природы, хотя он и самый древний, но требует еще своего научного обоснования.
Ниже рассматривается алгоритм разбиения единицы (целого) на такие оптимальные части, которые удовлетворяют известному опыту и эволюционным свойствам природы.
Целое – единица 1 разбивается на три множества по формуле полного набора вероятностей, где множества объедены операцией сложения в некоторую целостность:
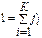(3)
где К- число рассматриваемых состояний системы; fi - вероятность каждого состояния; последовательность этих состояний i.
Разобьем далее это выражение целого предположением, что эти три множества К, fi i могут изменяться, не нарушая целостности системы, учитывая, что К мультипликативная величина и последовательность i не имеет значения.
Тогда целое единица разбивается на сумму двух функций:
= I+G, (4)
где 1 отражает целостность системы, I – мера хаоса описывает неопределенность процесса разбиения целого на множестве рассматриваемых состояний, G – мера порядка впервые описывает процесс определенности процесса разбиения целого на множестве рассматриваемых состояний. Мера хаоса I описывает реализованные состояния системы или бытие, а мера порядка G описывает запрещенные состояния или небытие. I и G - это новые математические функции, введенные автором в 1971 году для описания качества систем.
Пояснение. Систему можно задать на множестве рассматриваемых состояний К областью реализуемых I и запрещенных состояний G. Мера хаоса I описывает область разрешенных и реализуемых состояний, а мера порядка G описывает область запрещенных или нереализуемых состояний из К рассматриваемых состояний.
На рис 1. представлено графическое пояснение смысла функции I и G.
Соотношение между мерами хаоса и порядка в общем случае таково, что мера хаоса меньше или равна мере порядка в общем случае:
I ≤ G, (5)
так как всегда можно выбрать такое большое число рассматриваемых состояний К, в котором большая часть значений вероятностей событий равна нулю и число запрещенных состояний больше числа реализуемых состояний. Небытие всегда больше бытия.
Рис. 1. Графическое представление мер хаоса I и порядка G.
Перед тем как сделать следующий шаг разбиения целого на части, поясним смысл уравнения (4) в статистической механике.
Умножим на LnK уравнение (4) и получим уравнение:
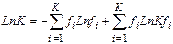= I*+G*, (6)
где LnK – безразмерная статистическая энтропия, I* - мера неопределенности состояния и G* - новая функция мера определенности состояния системы, К - число рассматриваемых микросостояний, fi -вероятность i -го микросостояния.
В теории вероятностей Н.Колмогорова не рассматривалась проблема сохранения целостности системы при изменении указанных трех множеств. Поэтому мера порядка в теории вероятностей не была введена.
При постулате Л.Больцмана о равновероятности допустимых микросостояний мера порядка G равна нулю. Поэтому постулат Л.Больцмана рассматривает частный случай связи энтропии (меры внутреннего превращения) с вероятностью реализуемых микросостояний, когда взаимодействием бытия и небытия можно пренебречь.
Кроме того, ранее автором обращено внимание на то, что равенство мер хаоса и порядка:
I*=G*= 1/2LnK=LnW (7)
включает в себя постулат Л.Больцмана как частный случай. Поэтому можно строить статистическую физику, начиная не с постулата Больцмана и Гиббса о микроканоническом распределении энергии W, а с постулата о равенстве мер хаоса и порядка (7).
Ниже поясним целесообразность выбора в новом способе описания систем постулата о равенстве мер хаоса и порядка в трех классах переменных.
В идеальном газе все степени свободы только поступательные, их вероятность достоверна и равна единице: f(п.с.с.)=1, а вероятности других степеней свободы – равны нулю: f (др,c.с.)=0, структурное пространство состояний имеет вырожденный вид:
К(l)= K( 1,0,0,….0 ), (8)
в этом случае мера хаоса по типам степеней свободы минимальна и равна нулю: I(l)=0, а мера хаоса по импульсам и координатам равна своему максимальному значению: I (p,q)=max.
Кроме того, в статистической механике постулировано рассмотрение в только двух независимых классов переменных: координат и импульсов. Мера хаоса I* описывает процесс рассеяния энергии в статистической механике, а мера порядка G* - впервые открывает возможность описывать процесс концентрации энергии в системе. Для равновесного идеального газа мера хаоса максимальна по координатам и импульсам и минимальна по типам степеней свободы, так все частицы обладают только поступательных степенями свободы. Соответственно мера порядка имеет минимальное значение по координатам и импульсам и максимальное значение по типам степеней свободы.
ИДЕАЛЬНЫЙ ГАЗ
I*(p,q) - max, I*(l) - min (9)
G**(p,q) - min, G*(l) - max
В модели идеального газа К - число микросостояний - задается как постоянная величина, определяемая в двух независимых классах переменных (p) и (q) - импульсов и координат: К=К(p,q)=К(p)К(q). При этих условиях в статистической механике постулируется молчаливо постоянство условий концентрации энергии в системе, процесс концентрации энергии не рассматривается, так как взаимодействие бытия и небытия исключено из рассмотрения постулатом Л.Больцмана.
Следующий шаг разбиения целого на части связан с введением третьего класса переменных l – набора типов степеней свободы, характеризующего структуру динамических элементов. Добавим в рассмотрение третий класс переменных (l), учитывающий кроме координат и импульсов другие распределенные параметры, например, набор типов степеней свободы, и будем рассматривать К как функцию:
К=К(p)К(q)К(l)= К(p,q,l). (10)
При таком способе описания систем постулат Л.Больцмана не выполняется, так как постоянно изменяется К(l) набор типов степеней свободы (l), и последовательность происходящих событий i. Изменение К приобретает свой самостоятельный глубокий смысл при описании эволюции сложных систем.
Предлагается рассматривать сложные системы по-новому, с помощью мер хаоса и порядка, где за счет изменения К изменяются условия концентрации и рассеяния энергии. То есть впервые учитывается взаимодействие бытия и небытия и это взаимодействие разбивает природу, как целое, на оптимальные части, которые не рассматривались ранее в известных моделях статистической физики и теории вероятностей.
Новым постулатом описания систем предложено принять постулат о равенстве мера хаоса и порядка в трех классах переменных:
I (p, q, l) = G (p, q, l), (11)
В этом случае имеем новый способ описания целостных систем с переменной внутренней организацией, где в целом процессы рассеяния и концентрации энергии уравновешены, мера хаоса описывает процесс рассеяния энергии, а мера порядка - процесс концентрации энергии, определенные в трех классах переменных.
Следующий шаг разбиения целого на части содержит рассмотрение взаимодействия процессов рассеяния и концентрации энергии между собой, описываемых мерами хаоса и порядка в трех классах переменных. Все возможные взаимодействия мер хаоса и порядка описываются симметрией:
∆I(p)+∆I(q)+∆I(l)=0. (12)
Насколько возрастает бытие по одним переменным, настолько же бытие убывает по другим переменным, при этом изменение меры хаоса, описывающей бытие, происходит не менее чем в трех взаимосвязанных классах переменных, где ∆I(p), ∆I(q), ∆I(l) - приращения энтропии по импульсам, координатам и структурному многообразию динамических элементов рассматриваемой системы.
Это равновесие целого указывает на возможность бесконечного изменения организации целостной системы по внутренним причинам и внутренним переменным типам степеней свободы, то есть оно впервые позволяет описывать самодвижение сложных систем в отличие от известных уравнений динамики.
Следующий шаг разбиения целого на части связан с выбором среди симметрии хаоса и порядка только необратимые изменения, которые удовлетворяют рекурсии по уравнению (2).
Этот шаг логичен, если предположить что актуальная бесконечность шагов рекурсии по уравнению (2) уже совершилась и из этой актуальной бесконечности рекуррентных шагов можно выбрать счетные необратимые шаги.
Рекурсия (2) описывает эволюцию отношения последующих структур к оптимальному отношению частей и целого по «золотому сечению»:
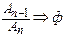,(13)
n>10 (три замкнутых цикла спирали развития) или к «золотой пропорции» при n→∞:
. (14)
Порядковый номер числа может быть произвольным, его значения пробегают от единицы до бесконечности: n=1,2,3,….∞.
Практическим примером этого случая в биологических и социальных системах является ряд Фибоначчи Fn:
0, 1, 1, 2, 3, 5,8,13,21,34,55,89,144,… (15)
«Золотое сечение» ф разделяет интервал [0-1] на части: [0- ф ] и [ ф -1], так что три интервала связаны между собой одним отношением ф. Выделение на интервале от нуля до единицы [0-1] третьей особой иррациональной точки ф очень важно. Эта точка ф указывает на бесконечную осцилляцию эволюции отношения параметров природы к ф для процессов, описываемых уравнением (4) и (12).
Важно, что развитие целого на оптимальные части не познается на основе натурального ряда чисел, 1, 2, 3, 4, 5…, где каждое число совпадает с его порядковым номером:
A(n)=n. (16)
Отношения числа A(n) к его последующему значению A(n+1) в натуральном ряде чисел пробегают значения от 0,5 к единице 1.
Это же отношения A(n) / A(n+1) для чисел ряда Фибоначчи описывают бесконечную осциллирующую закономерность, которая стремится к «золотому сечению»:
0, 1, 0.5, 0.6(6), 0.6, 0.625, 0.615, 0,619, 0,617 → ф. (16)
Каждое последующее отношение чисел в ряде Фибоначчи больше или меньше числа ф.
Итак, рассмотренный алгоритм разбиения целого на оптимальные части привел к рассмотрению взаимодействия бытия и небытия, описываемого процессами рассеяния и концентрации энергии в трех классах переменных с помощью мер хаоса и порядка. Этот алгоритм указывает на эволюцию этого взаимодействия к золотой пропорции между классами переменных и в каждом классе переменных по отдельности между их последующими значениями.
А теперь обратим внимание на то, что эти оптимальные части, устроенные по золотой пропорции, отражающие взаимодействие бытия и небытия, позволяют реконструировать многие постулированные положение статистической механики Больцмана-Гиббса и дополнить их новыми закономерностями об эволюции и развитии систем