Цель занятия – привить обучающимся практические навыки в расчетах коэффициентов парной корреляции для проведения исследований наличия линейной связи между двумя случайными величинами (СВ).
Задачи занятия:
1. Ознакомить обучающихся с основами корреляционного и регрессионного анализа, а также с методикой расчета коэффициентов парной корреляции.
2. Научить обучающихся самостоятельно проводить расчет коэффициентов парной корреляции с использованием персонального компьютера.
Теоретическая часть [2, 7, 16]
При анализе результатов экспериментальных данных по надежности часто приходится рассматривать распределение не только одной случайной величины (наработки на отказ), но и влияние на эту случайную величину другой случайной величины, т.е. приходится устанавливать, есть ли и какая взаимная связь двух случайных величин.
Если каждому значению хi соответствует определенное (может быть не одно) значение уi, то связь функциональная. Между случайными величинами кроме функциональной может существовать и стохастическая связь.
При стохастической связи одна из случайных величин реагирует на изменение другой или других случайных величин изменениями параметров закона распределения.
При оценке стохастической связи между двумя или несколькими случайными величинами определяют форму связи (криволинейная или прямолинейная) и силу или тесноту связи. Форма связи определяется регрессионным анализом, а теснота связи (степень взаимодействия) между случайными величинами – корреляционным анализом.
Стохастическую зависимость Y от X описывают условным математическим ожиданием (МОЖ).
¥
`Y(x) = M [ Y / X = x] = ò y¦ (y / x) dy. (2.5)
- ¥
В механической аналогии распределения, если единичная масса распределена на плоскости хоу с плотностью ¦ (х, у), `Y(x) есть ордината центра тяжести массы, распределенной на прямой Х = х.
Зависимость (2.5) дает наилучшее предсказание величины Y(x) по значению Х = х. Эта зависимость является линией регрессии. При исследовании линии зависимости (2.5) определяют форму связи случайных величин. Таким образом, регрессия Y по Х определяет изменение МОЖ Y при изменении Х.
Форма связи исследуемых величин зависит от физической сущности явления и может иметь вид прямой линии, параболы и т.д. Определение формы линии регрессии, соответствующей реальной форме зависимости, составляет принципиальный момент в изучении корреляции и регрессии. Глубокое знание исследуемых явлений, влияющих на отказы, зависимостей между этими влияниями способствует правильному выбору линии регрессии. Совершенно неправильно считать, что найденное (2.5) регрессионное уравнение (т.е. некоторая функциональная форма) будет наилучшим только потому, что оно дает хорошее приближение, хотя нисколько не соответствует реальным физическим или техническим связям. В любой регрессионной задаче в первую очередь следует рассматривать физически обоснованную конкретную функциональную форму независимо от того, была ли она получена с помощью аналитических выводов или благодаря какому-нибудь иному предварительному знанию свойств переменных. Вполне возможно, что для аппроксимации исследуемой функции понадобятся другие функциональные связи, даже если уже опробованные давали хорошее приближение.
Тесноту связи между случайными величинами при линейной корреляции оценивают корреляционным моментом (ковариацией) kxy и коэффициентом корреляции rxy.
Корреляционный момент представляет собой МОЖ произведения отклонений х и у от их МОЖ.
kxy = M [(x – Mx) (y – My)]. (2.6)
Так как kxy зависит от единиц измерения при изменении масштаба, то сам по себе он не может служить показателем связи. Поэтому рассматривают и связь нормированных отклонений
(x – Mx) / sx и (y – My) / sy,
в результате чего получают коэффициент корреляции
rxy = kxy / sx sy. (2.7)
Коэффициент корреляции может находиться в пределах
-1 £ rxy £ 1.
Чем ближе к нулю ½ rxy½, тем слабее линейная связь между величинами, чем ½ rxy½ ближе к единице, тем связь сильнее. При ½ rxy½ = 0 или близком к нулю линейная корреляционная связь отсутствует. При ½ rxy½ = 1 или близком к единице статистическая линейная связь становится функциональной.
Для проверки значимости коэффициента парной корреляции нужно сравнить его значение с табличным критическим значением r, приведенным в табл. 2.3 [7]. Если рассчитанное значение коэффициента корреляции больше или равно табличному, то есть основания полагать что между СВ существует линейная связь. Для использования табл. 2.3 необходимо знать число степеней свободы f = n – 2 и выбрать предельный уровень значимости α (доверительная вероятность), например равный 0,05.
Таблица 2.3
Критические значения коэффициента парной корреляции при α=0,05
| Число степеней свободы f | Критическое значение r | Число степеней свободы f | Критическое значение r | Число степеней свободы f | Критическое значение r |
| 0,997 | 0,602 | 0,486 | |||
| 0,95 | 0,576 | 0,444 | |||
| 0,878 | 0,553 | 0,433 | |||
| 0,811 | 0,532 | 0,423 | |||
| 0,754 | 0,514 | 0,349 | |||
| 0,707 | 0,497 | 0,273 | |||
| 0,666 | 0,482 | 0,217 | |||
| 0,632 | 0,468 | 0,195 |
Отсутствие линейной корреляционной связи не означает, что отсутствуют и другие формы связи. Криволинейная связь в этом случае может существовать и даже быть функциональной.
При криволинейной корреляционной связи теснота связи характеризуется корреляционным отношением rxy
Ö`1 - rxy = Ö`M {[ Y - `Y(x)]} / sy = s[Y - `Y(x)] / s. (2.8)
Из (2.8) следует, что -1£ rxy £ 1.
Преимущество корреляционного отношения перед коэффициентом корреляции состоит в том, что коэффициент корреляции оценивает тесноту связи лишь с линейной зависимости, а корреляционное отношение служит мерой тесноты связи любой формы, в том числе и линейной. Однако корреляционное отношение не позволяет определить конкретный вид кривой (гипербола, парабола, экспонента), наилучшего приближения экспериментальных данных.
Порядок корреляционного (регрессионного) анализа следующий:
1) для определения вида функции регрессии строят точки [x;`Y(x)] и по их расположению делают предварительное заключение о примерном виде функции регрессии, при окончательном решении принимают во внимание особенности, вытекающие из физической сущности решаемой задачи;
2) в зависимости от вида функции регрессии используют формулы (2.6) или (2.8) для определения тесноты связи;
3) неизвестные параметры уравнения регрессии ищут методом наименьших квадратов (возможно также применение метода максимального правдоподобия);
4) полученные параметры подставляют в уравнение выбранного вида функции регрессии и получают искомое уравнение регрессии.
Такими методами по результатам эксплуатации оценена надежность грузовых автомобилей ЗИЛ-130 и КамАЗ-5320.
Параметр потока отказов и неисправностей w, 1/100км, для автомобиля ЗИЛ-130:
w = -0,66 + 0,39b + 0,29g + 0,12kпр - 13·10l-4 + 16,8¦ + 65·10i-4 + 0,27П;
для автомобиля КамАЗ-5320:
w = -0,68 + 0,4b + 0,12g + 0,08kпр + 7·10l-4 + 23,2¦ + 12·10i-3 + 0,19П,
где b- коэффициент использования пробега, характеризующий коэффициент использования рабочего времени;
g - коэффициент использования грузоподъемности;
kпр - коэффициент использования прицепов;
l – длина ездки с грузом, км (при l³ 100км принято l= 100км);
¦ - коэффициент сопротивления качению;
i – среднее значение уклона дороги, %;
П – коэффициент помехонасыщенности маршрута.
Диапазоны изменения факторов:
Значение фактора……….b a k пр l ¦ i П
минимальное 0,45 0,75 0 15 0,014 3 1
максимальное 0,9 1,2 1,3 100 0,08 32 2
Значения w получены при коэффициенте множественной корреляции соответственно r = 0,89 и r = 0,93.
В нормативной документации на ремонт в качестве одного из показателей ремонтопригодности принята удельная трудоемкость
текущего ремонта Т ×10-3 человеко-часов. По результатам обработки статистики получено для автомобиля ЗИЛ-130:
Т = 1,84 + 36,3¦ + 25·10i-3 + 0,94П;
Для автомобиля КамАЗ-5320:
Т = 3,1 + 68¦ + 0,057i + 0,96П.
В качестве основного показателя долговечности в нормативной документации принят ресурс автомобиля до капитального ремонта Lкр тыс. км. Для автомобиля ЗИЛ-130 получено
Lкр = 398 - 1645¦ - 1,17i – 43,7П.
По приведенным регрессионным зависимостям подсчитаны значения параметра w потока отказов и неисправностей, трудоемкости Т текущего ремонта и ресурса Lкр автомобилей до капитального ремонта при средних значениях эксплуатационных факторов для автомобилей ЗИЛ-130 и КамАЗ-5320:
Автомобиль w Т Lкр
ЗИЛ-130 1,33 5,88 213
КамАЗ-5320 1,4 9,24 -
Методика проведения занятия
1. Обучающиеся самостоятельно изучают теоретическую часть.
2. Под руководством преподавателя обучающиеся рассчитывают коэффициенты парной корреляции по исходным данным, гипотетически полученным при выполнении лабораторной работы №1 и приведенным в табл. 2.4.
Таблица 2.4
Значения измеренных диагностических параметров
| y i u | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| y1u | 13,2 | 12,8 | 12,5 | 11,5 | 12,8 | 12,9 | 13,1 | 13,3 | 12,4 | |
| y2u | 10,5 | 10,4 | 10,6 | 9,5 | 9,8 | 9,7 | 11,1 | |||
| y3u | 0,11 | 0,08 | 0,6 | 0,22 | 0,15 | 0,1 | 0,12 | 0,25 | 0,09 | |
| y4u | 15,5 | 13,5 | 12,5 | 11,5 | 13,9 | 12,6 | ||||
| y5u | ||||||||||
| y6u | ||||||||||
| y7u | ||||||||||
| y8u |
В табл. 2.4 ni соответствуют номерам измерений следующих диагностических параметров y i u:
y1u – напряжение аккумуляторной батареи без нагрузки (при включенных потребителях), В;
y2u – напряжение аккумуляторной батареи под нагрузкой (работа стартера без заводки автомобиля), В;
y3u – переходное сопротивление контактов прерывателя, В;
y4u – напряжение на контактах «Б» и «Ш» реле-регулятора, В;
y5u – минимально устойчивая частота вращения коленчатого вала двигателя (КВД), мин-1;
y6u – угол замкнутого состояния контактов прерывателя при 1000 мин-1;
y7u - угол замкнутого состояния контактов прерывателя при максимальных оборотах двигателя, мин-1;
y8u – падение частоты вращения КВД при отсоединении шланга принудительной вентиляции двигателя, мин-1.
Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 г. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон. В общем случае расчетные формулы будут иметь следующий вид:
yi u = 
yi u / n;
Для расчетов используем программу PEARSON EXEL и персональный компьютер. Последовательность расчета коэффициентов корреляции между диагностическими параметрами y1u и y4u показана на рис. 2.1…2.3.
Рассчитанный коэффициент корреляции Пирсона получился равным: r1,4 = 0,364999. Его значение может лежать в пределах [-1;+1]. Для проверки значимости коэффициента парной корреляции его величину необходимо сравнить с критическим значением r (см. табл. 2.3). Найдем число степеней свободы f = n – 2; n - число наблюдений (в нашем случае n= 10) => f = 8 получаем критическое значение r = 0,632. Критическое значение r = 0,632 больше рассчитанного коэффициента корреляции
Рис. 2.1. Ввод исходных данных
Рис. 2.2. Формирование массивов
Рис. 2.3. Результат расчета
Пирсона, r = 0,36499 следовательно эти величины между собой линейно независимы. Если бы мы получили расчетное значение коэффициента корреляции со знаком «-» это бы говорило о том, что СВ находятся в обратной связи, т.е. при увеличении одной вторая бы уменьшалась. В конце занятия обучающиеся индивидуально сообщают преподавателю о полученных результатах, представляя расчеты и делая вывод о наличии или отсутствии линейной связи между всеми рассмотренными диагностическими параметрами.
Вопросы для самостоятельной работы
1. Что такое стохастическая связь между СВ?
2. Что такое функциональная связь между СВ?
3. От чего зависит форма связи?
4. Для чего используется корреляционный анализ?
5. Для чего используется регрессионный анализ?
6. В каких пределах изменяется коэффициент корреляции?
7. О чем говорит знак «-», полученный при расчете коэффициента корреляции?
8. Каким образом поступают в случае установления криволинейной корреляционной связи между СВ?
9. Что такое число степеней свободы и как оно определяется?
10. Что такое предельный уровень значимости?
11. Чем ограничивается диапазон использования регрессионных зависимостей?
Практическое занятие №3
ИССЛЕДОВАНИЕ ВЛИЯНИЯ СИСТЕМЫТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ И РЕМОНТА НА НАДЕЖНОСТЬ АВТОМОБИЛЯ
Цель занятия – ознакомиться с методикой разработки и реализации моделей процесса эксплуатации автотранспортных средств.
Задачи занятия:
1.Составить простейшую модель эксплуатации автомобиля.
2.Исследовать зависимость вероятностей состояний простейшей модели эксплуатации от пробега автомобиля.
3.Составить усложненную модель эксплуатации автомобиля.
4.Исследовать влияние продолжительности ТО и ремонта на надежность автомобиля.
Теоретическая часть
Техническая эксплуатация автомобилей представляет собой совокупность процессов работы в наряде, нахождении в техническом обслуживании, диагностировании, текущем и капитальном ремонте.
Для исследования процесса эксплуатации целесообразно применять марковские случайные процессы, которые предполагают, что вероятность любого состояния в будущем зависит от состояния машины в рассматриваемый момент времени и не зависит от того, когда и какими путями она пришла в это состояние [7, 12, 13].
Марковские случайные процессы для наглядности представляют в виде графов состояний (рис. 2.4). На графе определяются несколько состояний S 1, S 2, в которых может находиться машина в период ее эксплуатации. На графе их обозначают кружками, например состояние S 1 – работоспособное, а S 2 – неработоспособное.
Рис. 2.4. Граф состояний автомобиля
В течение эксплуатации машина переходит из одного состояния в другое, что на графе обозначается линиями со стрелками. Данные переходы характеризуются интенсивностями, например l – интенсивность возникновения отказов, m – интенсивность устранения отказов (проведение ремонтных работ).
Вероятность пребывания в каждом из состояний описывается уравнениями Колмогорова, которые составляют по следующему алгоритму [7]:
– в левой части размещается производная вероятности пребывания в соответствующем состоянии, например в состоянии S 1 (dP 1/ dt);
– в правой части записывается сумма произведений интенсивностей переходов на вероятности тех состояний, из которых происходят переходы.
Знак произведения положительный, если переход происходит в рассматриваемое состояние, и отрицательный – если машина переходит в другое состояние.
Согласно графу состояний (см. рис. 2.4), система уравнений Колмогорова имеет вид
dP 1(t)/ dt = -l P 1(t) + m P 2(t);
(2.9)
dP 2(t)/ dt = l× P 1(t)- m× P 2(t).
Так как из принятого условия машина может находиться лишь в одном из рассматриваемых состояний, то следует записать уравнение нормировки:
P 1(t)+ P 2(t) = 1. (2.10)
Одним из случаев марковского процесса является простейший поток событий, который характеризуется ординарностью, стационарностью и отсутствием последействия.
Поток является ординарным, если вероятность возникновения одновременно двух и более событий пренебрежительно мала по сравнению с возникновением одного события.
Стационарным называют поток событий, если вероятности возникновения событий не зависят от наработки с начала эксплуатации машины.
Поток без последействия характеризуется независимостью от числа ранее возникших событий и моментов из возникновения.
Интервал времени между двумя соседними событиями простейшего потока имеет показательное распределение:
f (t) = l×exp(-l t), (при t > 0) (2.11)
| где l – | интенсивность возникновения событий, обратная среднему значению наработки между событиями. |
Ординарный поток без последействия называется пуассоновским. Простейший поток – это стационарный пуассоновский поток [7].
Чтобы решить систему дифференциальных уравнений для вероятностей состояний, нужно задать начальное распределение вероятностей и приравнять их к 1: Р 1(0)+ Р 2(0) = 1.
Решать систему линейных дифференциальных уравнений целесообразно с помощью преобразования Лапласа [16]. Тогда уравнения с учетом начальных условий для изображений p i вероятностей Pi примут вид:
s p1=mp2 – lp1+1; s p2=-mp2 + lp1. (2.12)
Затем необходимо решить полученную систему алгебраических уравнений. В результате должны быть получены изображения искомых вероятностей:
; 
. (2.13)
Используя таблицы обратных преобразований Лапласа для рациональных изображений [16], получим решение системы уравнений:
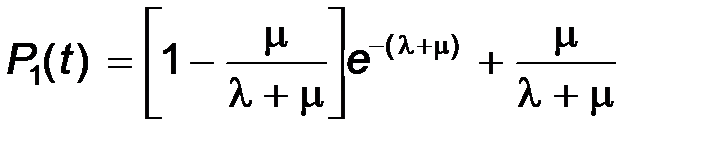; P 2(t) =1 – P 1(t). (2.14)
В настоящее время существует компьютерный математический пакет Mathcad, позволяющий производить символьные преобразования, в том числе прямое и обратное преобразование Лапласа, что существенно упрощает решение более сложных систем дифференциальных уравнений Колмогорова. Для этого стоит лишь сделать прямое преобразование Лапласа, решить полученные уравнения относительно изображений соответствующих вероятностей, а затем прибегнуть к помощи MathCad [14, 15]. В результате пользователь получает оригинал изображения (рис. 2.5).
Полученные выражения характеризуют изменение вероятностей нахождения системы в соответствующих состояниях в зависимости от наработки машины и являются моделью технической эксплуатации автомобиля.
Во многих случаях, когда процесс, протекающий в системе, длится долго, возникает вопрос о предельном поведении вероятностей при t ® ¥.
Рис. 2.5. Пример символьного обратного преобразования Лапласа
Если все потоки, переводящие систему из состояния в состояние, простейшие, то, как правило, существуют финальные (предельные) вероятности состояний, не зависящие от того, в каком состоянии находилась система в начальный период. Это означает, что с течением времени в системе устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний не меняются (рис. 2.6).
Рис. 2.6. График зависимости вероятности работоспособного
и неработоспособного состояний автомобиля от наработки
В этом предельном режиме каждая финальная вероятность характеризует среднее относительное время пребывания системы в данном состоянии. Система, для которой существуют финальные вероятности, называется эргодической.
Для определения финальных вероятностей нет необходимости решать системы дифференциальных уравнений, их можно найти непосредственно по графу состояний, приравняв левые части уравнений Колмогорова к нулю и отбросив зависимость вероятностей от наработки, т.к. определяются финальные вероятности состояний, например:
-l P 1 + m P 2 = 0; l P 1- m P 2 = 0. (2.15)
С учетом уравнения нормировки получаем:
; 
. (2.16)
Возможен способ решения с помощью символьных преобразований в системе MathCad (рис. 2.7). Для этого указывают начало решения системы уравнений с помощью слова Given, затем перечисляют уравнения системы, далее записывается слово Find (P 1, P 2) с указанием в скобках искомых переменных, добавляется стрелка и в пункте меню "Символы" выбирается подпункт "Расчеты" – "Символьные". За стрелкой появляется вектор решений системы.
Рис. 2.7. Символьные преобразования системы алгебраических уравнений
Методика проведения занятия
1. Исследование простейшей модели эксплуатации автомобиля.
1.1. Составить граф простейшей модели эксплуатации автомобиля, согласно которой автомобиль может находиться в работоспособном или неработоспособном состоянии.
1.2. Описать граф уравнениями Колмогорова.
1.3. Выполнить прямое преобразование Лапласа полученных дифференциальных уравнений.
1.4. Решить полученную систему алгебраических уравнений относительно изображений вероятностей состояний.
1.5. Выполнить обратное преобразование Лапласа с помощью компьютерной программы MathCad и составить модель процесса эксплуатации автомобиля.
1.6. Получить у преподавателя данные о средней наработке на отказ и среднем времени восстановления работоспособности автомобиля.
1.7. Построить и проанализировать зависимости вероятностей пребывания автомобиля в работоспособном и неработоспособном состояниях и по графику определить финальные вероятности состояний.
2. Исследование усложненной модели эксплуатации автомобиля.
2.1. Составить граф состояний усложненной модели эксплуатации, получив от преподавателя возможные состояния автомобиля в процессе эксплуатации и интенсивности переходов.
2.2. Описать граф уравнениями Колмогорова.
2.3. С помощью программы MathCad определить уравнения финальных вероятностей состояний путем символьных преобразований.
2.4. Исследовать влияние продолжительности пребывания машины в ТО, ремонте на коэффициент готовности автомобиля, предварительно построив графики указанных зависимостей, используя систему MathCad.
3. Сделать выводы.
Вопросы для самостоятельной работы
1. Что такое техническая эксплуатация автомобилей?
2. Что такое граф состояний?
3. Что такое марковский случайный процесс?
4. Последовательность составления уравнений Колмогорова.
5. Как решить систему дифференциальных уравнений Колмогорова с помощью преобразований Лапласа?
6. Что такое марковский простейший поток событий?
7. Объясните свойства простейшего потока: ординарность, стационарность, отсутствие последействия.
8. Что такое финальные вероятности состояний?
9. Как определить финальные вероятности состояний с помощью графа состояний?
Практическое занятие №4
ОБОСНОВАНИЕ РАЦИОНАЛЬНОЙ ПЕРИОДИЧНОСТИ ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ
ЭЛЕМЕНТА АВТОМОБИЛЯ
С ПОМОЩЬЮ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ
Цель занятия – изучить методику и получить навыки имитационного моделирования при определении периодичности ТО элемента автомобиля на ЭВМ с помощью системы MathCad.
Задачи занятия:
1. Изучить методику имитационного моделирования.
2. Получить задание и составить вектор исходных данных о наработке на отказ элемента.
3. Определить характеристики распределения наработки на отказ и периодичности ТО и выбрать законы распределения.
4. Составить протокол для выполнения статистических испытаний на MathCad и провести испытания.
5. Построить график зависимости вероятности безотказной работы от периодичности ТО и определить рациональную периодичность ТО.
Теоретическая часть
В том случае, если невозможно получить аналитическое решение задачи, в качестве метода исследования применяют статистическое моделирование [12, 13].
Основными этапами такого исследования являются: построение формальной модели изучаемого процесса, программное обеспечение процесса имитации траекторий модели и имитационные эксперименты.
Этап построения формальной модели сводится к составлению алгоритма формирования определенной последовательности, а также к определению реализаций процесса, получению на его основе необходимых характеристик.
Этап организации программного обеспечения заключается в создании компьютерной программы, позволяющей воспроизводить (имитировать) реализации модели в соответствии с найденными закономерностями и находить соответствующие показатели работы модели.
В качестве такой программы целесообразно использовать математический пакет MathCad [14, 15], который имеет множество необходимых функций для статистического моделирования: функции – генераторы случайных чисел, распределяющихся по определенным законам, функции для определения характеристик распределения случайных величин и т.п.
Этап имитационных экспериментов – это работа с моделью. На этом этапе осуществляется выбор модели из имеющихся альтернативных вариантов и способов обработки выходной информации для эффективного получения необходимых результатов.
Метод статистических испытаний дает возможность исключить влияние побочных факторов и сократить затраты времени и средств на выполнение испытаний.
Алгоритм определения оптимальной периодичности ТО с помощью статистического моделирования включает предварительное определение на основании имеющихся данных периодичности ТО и коэффициента вариации [12]. По результатам наблюдений или расчетным данным создаются два массива данных, содержащих сведения по наработкам на отказ и периодичности ТО. Из этих массивов случайным образом извлекаются реализации наработки на отказ и периодичность проведения ТО. Если наработка на отказ менее периодичности ТО, то фиксируется отказ, в противном случае проводится ТО машины. Данный опыт используется многократно, что позволяет получить статистическую информацию об отказах машины при выбранной периодичности ТО, а соответственно, и определить вероятность безотказной работы. В случае, если вероятность безотказной работы ниже заданного уровня, производится корректировка периодичности ТО и испытания повторяются заново.
Методика проведения занятия
1.На первом этапе по результатам наблюдений нужно определить вектор наработок на отказ автомобиля X:
| – вектор наработок на отказ исследуемого элемента автомобиля, км пробега. |
2. Далее определяют характеристики распределения наработки на отказ (см. рис. 2.8).
– среднее значение наработки, км, Х:=mean(X); X:=2465;
– среднеквадратическое отклонение, км,
GX:=Stdev(X); GX:=225;
– коэффициент вариации наработки на отказ VX:= 
VX =0.091.
Закон распределения наработки на отказ можно принять на основе визуального совпадения полигона опытного распределения с кривой дифференциальной функции или кривой накопленных опытных вероятностей с интегральной функцией закона (приложение 10).
Более оперативно закон распределения можно выбрать по коэффициенту вариации: для нормального закона коэффициент вариации находится в пределах 0…0,33, для закона Вейбулла – 0,3…0,7, для экспоненциального закона – около 1. Соответственно для предлагаемого примера закон распределения наработки – закон нормального распределения.
Более точно гипотеза о законе распределения может быть оценена с помощью критерия c2 [12] (приложение 11).
3. Параметры распределения периодичности технического обслуживания автомобилей принимаются на основе априорной информации, а некоторые рассчитываются:
– среднее значение периодичности ТО, км, L:=1700;
– среднеквадратическое отклонение периодичности ТО, км, GL:=200;
– коэффициент вариации периодичности ТО
VL:= 
; VL:=0.118.
По коэффициенту вариации принимаем закон распределения периодичности ТО – закон нормального распределения.
4. Статистические испытания производят в следующем порядке:
4.1. Число испытаний определяется с учетом заданной односторонней доверительной вероятности a (a:=0.99), допустимой относительной ошибки d (d:=0.05) и коэффициента t a, который рассчитывается по формуле
t a:= 
, (2.17)
| где x a – | квантиль нормального распределения наработки на отказ автомобиля, т.е. величина наработки, соответствующая заданной доверительной вероятности a. Используя встроенную функцию определения квантилей для нормального закона распределения MathCad, x a определяют по формуле x a:= qnorm(a, x, G). |
Тогда необходимое число испытаний будет рассчитано по выражению:
(2.18)
(функция ceil позволяет округлить результат до целого в большую сторону).
4.2. Статистические испытания проводятся с помощью встроенных функций случайных чисел, подчиняющихся заданным законам распределения пакета MathCad (rnorm (ni, x, GX) и другим) и позволяющих получить массивы наработки на отказ и периодичность ТО:
– получение массива (вектора) реализаций наработки на отказ Xr:
Xr:= rnorm (ni, x, GX); (2.19)
– получение массива (вектора) реализаций периодичности ТО Lr:
Lr:= rnorm (ni, L, GL). (2.20)
4.3. Определяется число отказов с помощью функции условия If, при этом считается, что отказ произойдет в случае, если ТО не будет своевременно произведено, т.е. реализация наработки на отказ будет меньше, чем реализация периодичности ТО, предварительно задается переменная – диапазон j:= 0… ni – 1:
RLj:= if (Xrj > Lrj,0.1), (2.21)
| где RLj – | переменная, регистрирующая отказы автомобиля: если Xrj > Lri, то отказ не происходит и переменная RLj= 0, в противном случае RLj = 1 (отказ произошел). |
Результаты испытаний сводятся в табл. 2.4.
Таблица 2.4
Результаты статистических испытаний (фрагмент)
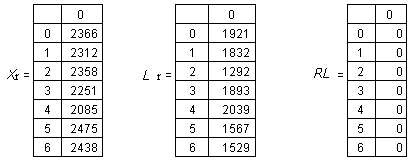
5. По данным испытаний производится расчет вероятности безотказной работы, соответствующей принятым характеристикам распределения периодичности ТО:
; P:= 0.995. (2.22)
6. Так как довольно сложно определить значение периодичности ТО, соответствующее заданной вероятности безотказной работы, то целесообразно сделать несколько испытаний при различных значениях периодичности ТО, изменяя значение L в п. 3, а затем графически определить искомое значение, как показано на рис. 2.8 и сделать выводы.
Рис. 2.8. Результаты испытаний и график зависимости вероятности безотказной работы от периодичности ТО автомобиля
Для этого создают вектор результатов испытаний Rez (приведен ниже), в первую колонку записывают значения периодичности ТО, а во вторую – вероятность безотказной работы, соответствующую периодичности. Предварительно вводят переменную – диапазон z:= 0…6.
7. Сделать выводы по проделанной работе.
Вопросы для самостоятельной работы
1. Основные этапы статистических испытаний.
2. Преимущества статистических испытаний.
3. Порядок выполнения работы.
4. Как создается вектор реализаций наработки на отказ автомобиля?
5. Как создается вектор отказов автомобиля в процессе испытаний?
6. Что такое вероятность безотказной работы автомобиля и ее расчет?
7. Порядок статистических испытаний.
8. Как ориентировочно выбрать закон распределения наработки на отказ автомобиля?
9. Как рассчитать статистические характеристики распределения?
10.Как рассчитать статистические характеристики распределения с помощью MathCad?
11.Что включает алгоритм определения оптимальной периодичности ТО с помощью статистических испытаний?
Практическое занятие №5
ОПТИМИЗАЦИЯ КОЛИЧЕСТВА ПОСТОВ СТО
Цель занятия – изучить методику и получить навыки оптимизации количества обслуживающих постов СТО методами теории массового обслуживания на ЭВМ с помощью системы MathCad.
Задачи занятия:
1. Изучить простейшие системы массового обслуживания, их особенности и расчет характеристик эффективности функционирования.
2. Изучить методику оптимизации количества постов СТО.
3. Выполнить оптимизацию с помощью системы MathCad и сделать выводы.
Теоретическая часть
При организации обслуживания автомобилей на станции технического обслуживания (СТО) необходимо учитывать возможные простои автомобилей, связанные с очередью, а также затраты на содержание обслуживающих постов. Очевидно, что при увеличении количества постов СТО происходит рост затрат на содержание оборудования, производственных рабочих, производственных площадей, но одновременно снижается время, а соответственно, и потери средств, связанные с простоем автомобилей из-за ожидания обслуживания.
Критерием оптимальности количества обслуживающих агрегатов является минимум целевой функции – суммарных затрат от простоя автомобилей на ТО и затрат на содержание обслуживающих постов [12, 13]:
С= С пр+ С сод® min, (2.23)
где С пр – потери от простоя автомобилей на ТО, руб./ч:
С пр= t сист с прl; (2.24)
| здесь С пр – | потери от простоя автомобиля в течение 1 часа, руб./ч; |
| l – | интенсивность потока заявок, 1/ч; |
| С сод – | затраты на содержание обслуживающих постов зоны ТО, руб./ч: |
С сод= nс сод; (2.25)
| здесь С сод – | затраты на содержание обслуживающего поста в течение 1 ч, руб./ч. |
Решение этой задачи во многом зависит от определения среднего времени простоя автомобиля на техническом обслуживании t сист, которое может быть рассчитано с помощью математического аппарата теории массового обслуживания [7, 16], так как совокупность обслуживающих постов является элементом обычной системы массового обслуживания.
Системы массового обслуживания (СМО) подразделяются на несколько групп [7]:
- открытые и закрытые; под открытыми СМО понимаются такие, у которых интенсивность