Иногда приходится складывать числа, группирующие-
ся вокруг одного и того же «корневого» числа. Особенно
часто такие процедуры приходится производить при об-
работке статистических измерений Допустим, необходи-
мо произвести сложение чисел
57+54+53+55+54+52+54+50 =.
Замечаем, что все эти числа близки к 54. Всего необхо*-
димо сложить 8 чисел. Сумму находим в следующей по-
следовательности:
1) находим сумму «корневых» чисел: 54-8 = 432;
2) находим сумму отклонений каждого числа от
корневого.
Если число больше корневого, отклонение берем со
знаком плюс, если число меньше корневого — со знаком
минус. Для приведенного примера сумма отклонений
Равна
3+0—1 + 1+0—2+0—4 = —3;
3) получившуюся сумму алгебраически прибавляем к,
результату первого пункта
432—3=429.
Выбор корневого числа не влияет на окончательный
результат. Так, если за корневое число было выбрано не
число 54, а число 55, то просто изменяются выкладки:
1) 55-8 = 440,
2) 2—1—2+0—1—3—1—5== —11,
3) 440—11=429.
Результат, вполне естественно, получается тот же.
За корневое число обычно стараются принять такое
число, чтобы наиболее просто находилась сумма откло-
нений.
Найдите самостоятельно следующие суммы:
1) 33+29+31+32+27+33+31+32+31+29+30 =
2) 46+47+48+43+45+44+41+46+45+44+39 =
3) 52+54+51+53+52+54+50+52+53+55+50=
Ответы для проверки: 1) 338; 2) 488; 3) 576.
3. ИСПОЛЬЗОВАНИЕ ПРИ СЛОЖЕНИИ МЕТОДА
СРЕДНЕГО ЧИСЛА
(формулы суммы арифметической прогрессии)
Частным случаем сложения с использованием корне-
вого числа является сложение чисел, образующих ариф-
метическую прогрессию..
Чаще всего встречаются тройки чисел, одно из кото-
рых меньше другого на а и больше третьего тоже на а,
например: 27+30+33. Здесь 30 больше 27 на 3 и меныше
33 на 3. В этом случае для нахождения суммы чисел до-
статочно умножить среднее число на число слагаемых]
30-3 = 90.
Правило применимо для любото нечетного числа сла-
гаемых:
31+32+33 = 32-3=-96;
23+20+17 = 20-3 = 60;
23+24+25+26+27 = 25-5=125;
52+56+60+64+68=60-5=300;
270+280+290+300+310+320+330 = 300-7 = 2100.;
Случаи, когда цифры или числа образуют правиль-
ную возрастающую или убывающую последовательность
(типа 31+32+33 или 23+20+17), обычно сразу броса-
ются в глаза, если же порядок следования нарушен
(13+17+15), то для автоматического выделения таков
тройки от вычисляющего требуется определенная мате-
матическая культура.
Если число членов арифметической прогрессии чет-
ное, то при суммировании используется формула для сум-
мы т членов арифметической прогрессии

говорящая о том, что сумма S членов арифметической
прогрессии равна полусумме крайних членов, умножен-
ной на число членов т:
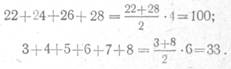
Иногда вычисление целесообразно вести по эквива-
лентной формуле 
что исключает столкновение с дробями, получающимися
после деления суммы первого и последнего членов ариф-
метической прогрессии на 2, как это случилось бы при
вычислении второго примера.
Решите самостоятельно:
1) 305+310+315+320-1-325+330= 2) 27+30+33+
+36+39+42+45+48= 3) 43+44+45+46+47 =
Ответы для проверки: 1) (305+330) -3=1905; 2) (27+
+48).4 = 300; 3) 45-5=225.
4. СОЕДИНЕНИЕ СОСЕДНИХ РАЗРЯДОВ ПРИ СЛОЖЕНИИ
И ВЫЧИТАНИИ
При определенном навыке выполнения вычислитель-
ных работ человеку не представляет труда складывать
Двузначные числа, сразу получая сумму. Можно ре-
комендовать складывать многозначные числа, соеди-
няя разряды. При обычном сложении сначала складыва-
ется младший разряд слагаемых и т. д. При достаточном
навыке можно складывать сразу 2 разряда (или даже
больше). Например, при сложении чисел
+
364 984
127 535
297 483
482 121
453 672
можно складывать сразу 2 младших разряда: 84+35=
= 119; 119+83 = 202; 202+21=223; 223+72 = 295
95 пишем, 2 запоминаем. Берем следующие.2 разряда
2+49+75=126 и т. д.
Совершенно аналогично этот прием используется и
при вычитании
_ 354 272
--206 539
72—39=33 записываем в окончательный результат
__ 354 272
--206 539
42<65, «занимаем» сразу единичку из старшего раз-
ряда, получаем 142—65 = 77
34—20=14
_ 354 272
206 539
7 733
__ 354 272
206 539
147 733
Решите самостоятельно, предварительно бегло оцен
вая, со сколькими разрядами целесообразно работать
(при нахождении разности часто достаточно просто ра-|
ботать с тремя разрядами):
1)
+
354 143
152 931
472 664
2)
+
113.947
254 764
129 643
888 354
3) _ 473 734
392 425
4)3724693 769241
Ответы для проверки: 1) 1 354 861, 2) 1 386 708; 3) 81 209
4) 955 452.
 5. ИСПОЛЬЗОВАНИЕ ОКРУГЛЕНИЯ ЧИСЕЛ
5. ИСПОЛЬЗОВАНИЕ ОКРУГЛЕНИЯ ЧИСЕЛ
ПРИ СЛОЖЕНИИ И ВЫЧИТАНИИ
(метод использования «круглых» чисел)
Если в вычислениях участвуют числа вида (а- 10п—в),
где в — мало, то вычисления можно упростить.
Допустим, нам необходимо сложить числа
253
+1 98
Рассуждаем следующим образом. 198 — это 200 без 2.
Вместо 198 прибавляем 200 (253 + 200 = 453) и из полу-
ченной суммы вычитаем то число, которое было добавле-
но первоначально к слагаемому, т. е. 2: 453—2 = 451.
Рассмотрим еще пример:
789
+395
Рассуждаем аналогично: 395=400—5. Складываем
789+400=1189 и вычитаем число, добавленное к слагае-
мому, 1189—5=1184.
Рассуждения могут быть и несколько иными. При
сложении чисел
253
+ 198
мы прибавляем ко второму числу 2 и столько же вычита-
ем из первого слагаемого
+200
При вычитании числа, близкого к круглому,
759
- 397
выбираем один из двух методов вычислений, приводящих
к одному и тому же результату:
1) к уменьшаемому и вычитаемому прибавляем до-
полнение числа 397 до 400, а уже затем производим вы-
читание:
759+3=762,
397+3=400,
762—400=362;
2) из уменьшаемого (759) вычитаем круглое число
(400)
__759
400
359
и вносим необходимую поправку
359+3=362.
Несколько примеров на использование приема:
354—182 = 366—200 =166, 451 — 193=458—200 = 258,
125 —89= 136— 100 = 36, 743— 79 = 764—100=664
Для закрепления навыка проделайте самостоятельно
вычисления:
1) 793+179= 3) 923—588= 5)495+495= 7) 455—187=
2) 354+295= 4) 154—95= 6) 259 + 379 = 8) 361-298=
Ответы для проверки: 1) 972; 2) 649; 3) 335; 4) 59|
5) 990; 6) 638; 7) 268; 8) 63.
6. ВЫЧИТАНИЕ ИЗ ЧИСЕЛ ВИДА а-10п ИЛИ а-10п+а,
ГДЕ а МАЛО
При вычитании из числа вида а-10п воспользуемся
понятием дополнения числа. Под дополнением данной
числа будем понимать разность между той степенью де
сяти,'показателем которой является число знаков этого
числа, и самим числом. Например, дополнением чнсла
89 является
100—89=11.
Под дополнением данного числа В до числа А будем
понимать разность А— В. (Подробно метод дополнений
описан в пункте 6 гл. II). Если необходимо произвести
вычитание
а) _ 4000 б) _ 2000
2238329
поступаем следующим образом.
Вычисление начинаем со старшего разряда. Из стар-
шей цифры уменьшаемого (или из нескольких первых
цифр уменьшаемого) вычитаем соответствующий разряда
вычитаемого, увеличенный на 1,
а) 4—(2+1) = 1 _4000 б) 20—(3+1) = 16 _2000
_2238 329
1... 16....
Каждый последующий разряд (кроме последнего) на-
ходится вычитанием соответствующей цифры вычитае-
мого из 9:
а) 9—2 = 7 _4000 б) 9—2 = 7 _2000
9—3 = 6 2238329
176... 167...
Последний знак находится вычитанием последней циф-
ры вычитаемого из 10:
а)_3000 б) __2000
1238 ___ 129
1762 1871
Процесс свелся, как нетрудно догадаться, к нахож-
дению дополнения числа 2238 до числа 4000 (или 329 до
2000). В дальнейшем мы неоднократно будем сталки-
ваться с необходимостью нахождения дополнения числа
до числа 10п или а- 10п, и поэтому желающему научиться
быстро считать совершенно необходимо уметь без затруд-
нений находить соответствующие дополнения и опери-
ровать с ними.
Найдем дополнение числа 7953 до числа 35 000
_ 35 000
7 953
1) находим 35—(7+1) =27
7 953
27...
2) находим дополнение числа 953
_ 1 000
953
047
окончательный ответ
_ 35 000
7 953
27 047
То, что в описываемом методе разность получается
сразу, начиная со старшего разряда, и все разряды по-
лучаются последовательно, делает метод пригодным для
устного вычисления разности многозначных чисел, если
уменьшаемое имеет вид а- 10п,
Освоив нахождение дополнения, - можно вычитание
свести к сложению: для того чтобы из какого-либо числа
вычесть другое число, достаточно к первому числу при -
бавить дополнение второго числа и из полученной сум-
мы вычесть дополняемое число (10п).
Число, выраженное через дополнение, записывают
следующим образом: пишут дополнение числа, а впере-
ди него ставят 1, наверху которой ставят знак «минус»
При таком изображении число 7839 запишется как]
-12161.
Разность чисел
_ 35 425
9 837
проще найти, сведя вычисления к нахождению суммы
35425
+ 10163
25 588
Записывать второй раз (через дополнение) пример
не нужно, пишем сразу ответ, начиная со старшего раз-
ряда, мысленно имея перед собой число в виде его до-
полнения и даже не все число, а только тот разряд, ко-
торый сейчас вычисляется:
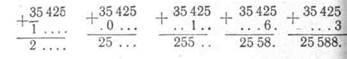
|
К описываемому приему сводится и вычитание из чи|
сел видаа»10п+а. Вычитание ведется из числа а - 10п, 1
ватем разность увеличивается на а:

|
+
200 011
197 785
02215
11
2 226
+
350 007
49 394
300 606
7
300 613
Найдите самостоятельно разности чисел:
1) 35000
— 24 359
2)
10 000
-2 397
3) 123 000
-52 395
4) 95 005
-12 934
Начало решения первого примера
_ 35 000
25...
10 ...
Ответы для проверки: 1) 10 641; 2)7603; 3) 70605;
4) 82 071.

 Глава ||
Глава ||
МЕТОДЫ, УПРОЩАЮЩИЕ
УМНОЖЕНИЕ И ДЕЛЕНИЕ
 орядок действий при вычислении произве- дения обычно подчинен следующему правилу Пишут первый сомножитель, который называется
орядок действий при вычислении произве- дения обычно подчинен следующему правилу Пишут первый сомножитель, который называется
множимым. Под множимым пишут второй сомножитель,
который носит название множителя, причем множитель,
подписывается так, чтобы его единицы стояли под едини-
цами множимого, после этого умножают множимое на|
каждую цифру множителя, начиная с единиц; получен-
ные частные произведения записывают одно под другие
отступая каждый раз на одну цифру влево и, наконец
складывают эти произведения.

1 ИСПОЛЬЗОВАНИЕ ПОРЯДКА ВЫПОЛНЕНИЯ ДЕЙСТВИЙ
ДЛЯ ОБЛЕГЧЕНИЯ ВЫЧИСЛЕНИЯ ПРОИЗВЕДЕНИЯ
Такой многолетиями сложившийся порядок умноже-
ния не является обязательным, а часто и рациональным
Иногда (эти случаи мы рассмотрим ниже) определеные
преимущества дает умножение, начиная со старшего
разряда множителя. В этом случае умножение ведется
так же, начиная с младшего разряда множимого Нача-
ло вычислений в приведенном примере будет следующее
2351 х 2351 х 2351'
| X |
234234234
..2... 02 4702
Разница будет только в том, что последовательно по-
лучающиеся частные произведения будут подписываться
с отступлением каждый раз на 1 разряд вправо. (Едини-
цы частного произведения пишутся под той цифрой, на
которую идет умножение.) Закончим вычисление нашего
примера:

Собственно говоря, совершенно неважно, как будет
записан множитель (Х2351 или Х2351) и как будет за-
234 234
писано первое частное произведение (под какой цифрой
будет записан младший разряд). Важно только правиль-
но записать последующие частные произведения.
Можно рекомендовать вообще сомножители записы-
вать в строку:
2351X234.

|
| Вторая форма записи приведет к следующему виду: |

|
Такая запись удобна тем, что не накладывает каких-
либо ограничений на последующие вычисления. Если мы
сочтем целесообразным первую форму записи, то
будет выглядеть так:
В любом случае младший разряд первого частного про-
изведения удобно записывать под младшим разрядом
множимого.
, Однако если в множителе более трех знаков, то
запись произведения в строку рекомендовать не стоит,
так как при таком расположении при отсутствии доста-
точного опыта вычислений цифра множителя, на которую
множат, легко ускользает от внимания. Исключение сто-
ит делать только тогда, когда среди цифр множителя
имеется единица (этот случай будет рассмотрен ниже),
Ниже будет показано, как та или иная последова-
тельность умножения упрощает вычисление.
Порядок действий в случае, когда цифры множителя
делятся друг на друга. Если в множителе имеются циф-
ры, делящиеся друг на друга, то следует принять такой
порядок действий, при котором пришлось бы сначала
умножать на меньшую из этих цифр. Например, в при-
мере
1234X239
целесообразно производить умножение, начиная со стар,
шего разояда.

Теперь нет необходимости умножить на 9 — достаточно
предыдущее частное произведение умножить на 3:
1234X239
2468
3702
+ 11106 (3072X3=11106)
Умножение на меньшую цифру всегда выполняется про
ще, с меньшими усилиями.
В примере 9532X8374 целесообразно начинать вычис-
ления с младшего разряда, что заменит в конце умноже
ние на 8 умножением первого частного произведения на
2. В примере 1935X379 правильнее начать вычисление
со старшего разряда.
Несколько примеров на использование приема:
1213X2483215X653
2426 9 645
+ 4852 (2425Х2=4852)+16 075 (9645*2=19290
9704 (4852X2 = 970 4) 19 290
300 824 2 099 395
Не менее, а скорее даже более, интересен случай,
когда часть множителя делится на одну из его цифр:
87 025
* 369
Нетрудно заметить, что 36=4X9, а 9 уже имеется в
множителе. Поэтому умножение начинаем с младшего
разряда и используем данную особенность:
87 025
* 369
783 225
+ 3 132 900 (783 225X4 = 3 132 900)
32 112 225
При нахождении произведения
* 5642
742
используем тот факт, что 42:7=6,
5642
* 742
+ 39494
236 964 (39 494X6 = 236 964)
[Решите самостоятельно:
1) 3512X637= 3) 2954X9234= 5) 5492X735=
2) 1253X728= 4) 7591X 348= 6) 4673X2642 =
Ответы для проверки: 1) 2237 144; 2) 912 184;
3) 27 277 236; 4) 2 641 668; 5) 403 662; 6) 12 346 066.
Порядок действий в случае, когда в множителе встре-
чается цифра, равная сумме двух других цифр множите-
ля. Здесь не требуется особого описания после предыду-
щего пункта, поэтому можно ограничиться примером с
[соответствующим пояснением:
5234X257
Замечаем, что 2+5=7, поэтому начинаем умножение со
СТаРШего разряда:
5234X257
10 468
26170
Теперь умножение на 7 заменяем сложением чисел
10468+26170 (так как 5234*2+5234*5=5234*(2+5) =
36638).
5234X257
10 468
+ 2 6170
36638
Практически этот прием стоит применять только в
том случае, когда одна из цифр равна сумме двух других
цифр, следующих друг за другом. Метод рационально
употребить, умножая на числа 2579, 87 134, 853.Если же
надо умножать на число, где складываемые частные про.
изведения разделены другими цифрами, то метод теряет
свои преимущества. Сам вычисляющий должен решить,
выгодно ли ему применить прием, умножая на числе
2 3 7 19 или на число 9 4 7 5.
Умножьте самостоятельно:
1) 7345X4437= 2) 1234X3528= 3) 3543X3376=
Ответы для проверки: 1) 32 589 765; 2) 4 353 555
3) 11961 168.
Порядок действий, когда множитель начинается или
кончается единицей. В этом случае порядок умножена
должен быть такой, чтобы вычисления начинались
умножения на единицу. При этом частное произведена
множимого на единицу не записываем, а принимаем ]
него само множимое. Только надо быть внимательным
ине забыть его учесть при нахождении суммы частных
произведений
2357X133.
Так как множитель начинается с единицы, то умножение
начинаем со старшего разряда:
2357X133
+ 7071
7071..
313481
В примере 3247X231 умножение начинаем с младшего
разряда:
3247X231
+9741
6494
750057
Обладая определенными навыками, этот же метод можно применять и тогда, когда цифра 1 стоит в середине множителя:
2244X213.
В данном примере неважно, с младшего или старше-
го разряда будет начато умножение. Для определенно-
сти примем вариант умножения с младшего разряда.
Найдя частное произведение 2244X3=6732, подпишем
его так, чтобы относительно него множимое (которое вы-
полняет роль, второго частного произведения) было сдви-
нуто влево на 1 разряд (т. е. второе частное произведе-
ние должно быть смещено вправо -на 1 разряд относи-
тельно множимого):
2244X213
6732
Частное произведение 2244X2=4488 должно быть сдви-
нуто на 1 разряд влево относительно множимого:
2244X213
+ 6732
4 488
477 972
Решите самостоятельно:
1) 3527X129= 2) 1274X2154= 3) 3594X3511 =
Ответы для проверки: 1)454 983; 2) 2 744 196;
3)12 618 534.
Выбор множителя. Если необходимо выполнить про-
изведение двух чисел, то мы можем выбрать в качестве
множителя любой из двух сомножителей. Освоив все
изложенное в первых 4 пунктах, нетрудно сформулиро-
вать основные положения, которыми можно руководст-
воваться при выборе множителя:
а) при прочих равных условиях за множитель лучше
убрать число, в котором меньше разрядов.Например, при
нахождении произведения чисел 375X4795 за множи-
тель целесообразно принять число 375. Это сократит вы-
числения;
б) если нет других соображений, берите в качестве
Множителя число с меньшими цифрами. В произведени-
ях 479X235; 783X283 целесообразно взять за множитель
второе число;
в) в качестве множителя целесообразно брать число,
в котором имеется единица, одинаковые цифры, цифры,
являющиеся суммой других цифр, или цифры, делящие-
ся на другие цифры этого числа.
При умножении чисел 354X1337 за множитель
целесообразно принять второе число, хотя в нем и боль-
ше разрядов. Но на единицу мы умножать не будем (ис
пользуем множимое), умножение на 3 выполним один
раз, а второй раз перепишем полученный уже результат
Для наглядности решим этот пример, принимая за мне
житель сначала первое число, а затем второе:
1 337X35 4 354X1337
5348 1062
+ 6685 + 1062
4011 2478
473298 473 298
Времени на второе вычисление уходит меньше за счет
того, что вычисляется на одно частное произведение
меньше, чем в первом случае.
Подумайте, какой из сомножителей в приведению
ниже примерах целесообразно принять за множитель и
почему: 1) 359X271= 2) 3749X2396=3) 179X123=
4) 437X475= Ответы: 1) второй сомножитель (не надо
умножать на 1); 2) второй сомножитель (можно заме
нить умножение на 6 умножением на 2 и умножение на
9 умножением на 3); 3) второй сомножитель —в нем
меньшие цифры; 4) первый сомножитель — умножен
на 7, можно заменить сложением произведений 475*3
475X4.