(«метод отрицательных цифр»)
Хорошо известно, что умножать на цифры 1, 2, 3, 4
легче, чем на цифры 6, 7, 8, 9. Ниже излагается метод,
позволяющий сводить умножение на 9 умножением на 1,
Умножение на 8 умножением на 2 и т. д. Этот прием ча-
ще используется при работе с арифмометром, но и при
письменном нахождении произведения может упростить
выкладки. Заменяем каждое из чисел б, 7, 8, 9 разностью
10-4, 10—3, 10—2, 10—1, записываем их в виде суммы
10+4, 10 + 3, 10+2, 10+1, обозначая отрицательные чис-
ла знаком «минус» сверху. Теперь любое натуральное-
число можно записать, не пользуясь цифрами 6—9. На-
пример, вместо 27 пишем 33, вместо 168 пишем 232, вме-
сто 2994 пишем 3014. Применяя такую запись многознач-
ного множителя, мы будем иметь наряду с обычными
положительными частными произведениями также
частные произведения отрицательные. Пример такого ум-
ножения с применением «отрицательных цифр»:
82 467 82 467
X 2984 Х3024
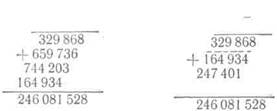
|
Находя итоговую сумму, учитываем, что некоторые
частные произведения (в нашем примере 164934) надо не
складывать с остальными частными произведениями, а
вычитать.
Поясним метод двумя примерами на использование
«отрицательных цифр»:
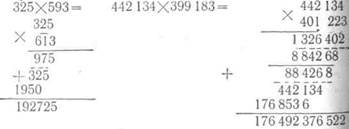
6. УМНОЖЕНИЕ ЧИСЕЛ, БЛИЗКИХ К 10*.
2-10п, 5 10п, А 10п
(метод дополнений)
Одним из самых эффективных и эффектных мето-
дов, используемых при необходимости перемножить два
числа, близких к 10п, является метод дополнений. Под
дополнением числа В до числа Абудем понимать раз
ность А— В (смотри гл. I, пункт 6). Обозначим ее че-
рез а. Из определения видно, что дополнение может быть
как числом положительным, так и числом отрицатель-
ным. Например, дополнение числа 95 до число 100 равно
5, а дополнение числа 103 до числа 100 будет — 3. Суть
метода дополнений проще всего рассмотреть на примере
умножения двух чисел, близких к 100.
У множение чисел, близких к 100. Предположим, надо
умножить 94><98
Дополнением множимого до 100 будет а1= 100—94 = 6,
дополнением множителя до 100 будет а2= 100—98 = 2.
Запишем это для наглядности так:
94X98
6 2
Чтобы получить произведение двух чисел, близких к 100,
необходимо:
1) из любого сомножителя вычесть дополнение второ-
го сомножителя до 100
98—6=92 или 94—2=92;
2) найти произведение дополнений
6X2=12;
3) к разности сомножителя и дополнения приписать
полученное произведение дополнений
94X98=9212.
Упрощение в вычислениях очень существенное.
Несколько примеров на умножение двузначных
чисел:
99X95= 1) 99—5=95—1=94,
1 5 2) 5X1=5,
3) 99X95=9405
(обратите внимание на то, что при приписывании произ-
ведения дополнений оно должно занимать два разряда)
91X98= 1) 91—2=98—9=89,
9 2 2) 2X9=18,
3) 91X98 = 8918.
99X84= 1) 84—1=99—16=83,
1 16 2) 1X16=16,
3) 99X84 = 8316.
Римеры для самостоятельного решения:
1) 94Х98= 3) 91X97= 5) 97X97= 7)98X89 =
2) 99Х99= 4) 97X85= 6) 93X96= 8)99X87=
Ответы для проверки: 1) 9212; 2) 9801; 3) 8827; 4) 8245;
5) 9 409; 6) 8928; 7) 8722; 8) 8613.
Умножение чисел, близких, но меньших 10п. Сформу-
лируем общее правило для перемножения чисел, близ-
ких к 10п. Чтобы перемножить два числа, близких к 10п
(например, 997X998), необходимо:
1) найти дополнение каждого числа до 10п
1000—997 = 3,
1000—998 = 2;
2) из одного из сомножителей вычесть дополнение
второго сомножителя до 10п
997—2=995 или 998—3=995;
3) найти произведение дополнений
3X2 = 6;
4) результат, полученный во втором пункте, умно-
жить на 10п (приписать п нулей) и к полученному произ-
ведению прибавить произведение дополнений
995X1000+6 = 995006.
997X998 = 995 006.
Последний пункт можно сформулировать по-другому:
4а) к результату, полученному во втором пункте,
приписать произведение дополнений, следя за тем, что-
бы оно занимало бы столько же разрядов, сколько их в
числе, к которому приписывается произведение.
Два примера для закрепления метода:
99 991X99 995= 9973X9997=
1) 100 000—99 991=9, 1) 10 000—9973=27,
100 000—99 995=5, 10 000—9997=3,
2) 99 991—5=99 986, 2) 9973—3 = 9970,
3) 9X5 = 45, 3) 27X3=81,
4) 99 991X99 995 = 9 998 600 045,
4) 9973X9997 = 99 700081.
Примеры для самостоятельного решения:
1) 999X999= 4)9 999 989X9 999 991 =
2) 9909X9990= 5) 9951X9991 =
3) 9988Х9997«6) 9911X9999 =
Ответы для проверки: 1) 998 001; 2) 98 990910;
3) 99 850 036; 4) 99 999 800 000 099; 5) 99 420441;
6) 99 100 089.
При решении примеров необходимо обращать особе
внимание на число разрядов, отводимых в окончатель-
ном результате для произведения дополнений.
Обоснование метода.
Предположим, что необходимо перемножить два чис-
ла х и у, причем ах— есть дополнение х до 10п, ау-
дополнение у до 10п, т. е. х+ах = 10п и y+ау=10п Тог-
да х*у=(10п-ах)-(10п-ау)= (10п-ах-ау)* 10п+ах+ау
= (х— ау) • 10п+ах- ау = (у—ах) • 10п+ах- ху.
расшифруем полученные результаты:
у-ах— разность между одним из сомножителей и допол-
нением второго сомножителя до 10п.
Наличие множителя 10п говорит о том, что произведение
•пополнений ах-ау можно «приписать» к разности (у —ах),
если это произведение представляет собой число, в кото-
ром не более п цифр.
умножение чисел, близких, но больших 10п. Для пе-
ремножения чисел, близких, но больших 10п, воспользу-
емся без изменения правилом, изложенным выше. Необ-
ходимо только помнить, что «дополнение» — величина
алгебраическая.
Итак, чтобы перемножить два числа, близких к 10п
(например, 104Х102, где п = 2), необходимо:
1) найти дополнение каждого из сомножителей до 10п
100—104 = —4,
100—102 = —2;
2) из одного из сомножителей вычесть дополнение
второго сомножителя до 10п
104—(—2) = 102—(—4) = 106;
3) найти произведение дополнений
(-4)Х(-2)=8;
4) к результату, полученному во втором пункте, при-
писать произведение дополнений, следя за тем, чтобы оно
занимало п разрядов
104 X 102=10 608.
Несколько поясняющих примеров
1003X1021= 1098—1099 =
1) 1000—1003 = —3 1) 1000—1098 = —98,
1000—1021=—21, 1000—1099 = —99,
2) 1021 — (—3) = 1024, 2) 1098—(-99) = 1197,
3) (-З)Х(-21)=63, 3) (—98)X(-99) =9702,
4) 1003Х1021 = 1 024 063. (произведение находим, ис-
пользуя метод дополнений)
4) 1098X1099=1197
+ 9702
1 206 702.
Примеры для самостоятельного решения:
1) 109Х10З= 4) 100 354X100 002 =
2) 12001Х10004= 5) 12331X10003 =
3) 221X104= 6) 1008X1008 =
Ответы для проверки: 1) 11227; 2) 120058004.
3) 22984 4) 10 035 600 708; 5) 123346993; 6) 1016064.
Перемножение чисел вида 10п+х. В предыдущем раз-.
деле мы рассмотрели, по сути дела, перемножение имен-
но таких чисел, но с оговоркой, что х мало. Снимем это|
ограничение. В этом случае может случиться, что устно I
ответ получить не удастся, но умножение сведется к чис-
лам, которые на порядок меньше первоначальных.
Пусть необходимо перемножить числа 142 и 123.
Будем поступать согласно рекомендациям предыдущего
раздела:
1) находим дополнения сомножителей до 10п (в на-
шем случае до 100)
100—142 = —42,
100—123 = —23;
2) из одного из сомножителей вычитаем дополнение
второго сомножителя
123— (—42) = 165 или 142—(—23) = 165;
3) к полученному результату приписываем произве-
дение дополнений

(необходимо внимательно следить за числом знаков, от-
водимых под произведение дополнений, иначе получим
ошибочный ответ 165 966). Найти в уме произведение
чисел 42 и 23 затруднительно, поэтому это вычисление
выполнено «в столбик», но использование метода допо-
нений позволило свести умножение трехзначных чисел к
умножению чисел двузначных.
В данном варианте использования метода дополне-
ний необходимо особенно внимательно следить за тем
чтобы в приписываемом произведении дополнений было
бы знаков на 1 меньше, чем в числе, к которому оно
приписывается. Поясним это на примере:
183X125
1) 100—183 = —83,
100—125==—25,
2) 183—(—25) = 125—(—83) =208,
3) (-83) X (-25)-2075.
Вот здесь важно не ошибиться. В числе, к которому не-
обходимо приписать произведение дополнений (208), три
знаа, а в приписываемом числе—четыре. Нетрудно до-
гадаться, как надо поступить в этом случае
208
+ 2075
22 875
Итак, 183X125=22 875.
В предыдущем разделе отмечалось, что число, знаков
для приписываемого произведения должно быть равно
числу знаков в числе, к которому оно приписывается.
Здесь же говорится, что число знаков для приписывае-
мого произведения должно быть на 1 меньше. Здесь нет
противоречия. В обоих случаях число разрядов, отводи-
мых под произведение дополнений, равно п. Если число
меньше 10п, то в нем п знаков. Если число больше 10п,
то в нем (п+1) разряд.
Примеры для самостоятельного решения:
1) 153X121= 3) 253X109= 5) 10354X10021 =
2) 1037X1037= 4) 131X124= 6) 153X153 =
Ответы для проверки: 1) 18513; 2) 1075369; 3) 27577;
4) 16244; 5) 103 757 434,6) 23409,
Умножение чисел, близких к 10п, одно из которых
больше 10п, а другое — меньше 10п. Посмотрим, как
можно применить метод дополнений в данном наиболее
сложном случае. Канва рассуждений остается та же.
Для того чтобы перемножить 2 числа, близких к 10п,
одно из которых больше 10п, а другое — меньше 10п (на-
пример, 107X95), необходимо:
1) найти дополнение каждого из сомножителей до 10п
100—107=—7,
100—95=5;
2) из одного из сомножителей вычесть дополнение
второго сомножителя до 10п
107—5 = 95—(—7) = 102;
3) найти произведение дополнений
(—7)Х5=—35.
Произведение получилось отрицательным. Поэтому при-
дется вспомнить, что на с. 38 последний пункт имеет еще
более строгую трактовку;
4) Результат, полученный в пункте 2, умножить на
10п (т. е. приписать к результату, полученному в пунк
те 2, п нулей) и к полученному произведению прибавить
произведение дополнений. Нетрудно сообразить, чтоэтот
пункт остается в силе, если под суммой понимать сумму
алгебраическую.
Проще это можно, наверное, сформулировать следую
щим образом в двух пунктах:
4) вычесть из 10п произведение дополнений
100—35=65;
5) к результату, полученному в пункте 2 и уменьшен,
ному на единицу, приписать результат вычислений пунк-
та 4
107X95=10165.
Два примера для закрепления навыков применения дан-
но го метода:
10 024X9998 =
1) 10 000—10 024 = —24,
10 000—9998 = 2,
2) 10 024—2 = 9998—(—24) = 10 022,
3) —24X2 = —48,
4) 10 000—48=9952,
5) 10 024X9998=100 219 952.
121X99 =
1) 100—121=—21,
100—99=1,
2) 121 —1=99—(—21) = 120,
3) —21X1==—21,
4) 100—21=79,
5) 121X99=11979.
В практике возможны случаи, когда произведение
дополнений будет по абсолютной величине превышать
10п. В этом случае надо пользоваться не пунктами 4и 5
а основной формулировкой: результат, полученный в
пункте 2, умножить на 10п и из полученного произведи
ния вычесть произведение дополнений:
2032X997=
1) 1000—2032=1032,
1000—997 = 3,
2) 2032—3 = 2029,
3) —1032X3 = 3096,
4) 2029Х103 = 2 029 000,
2 029 000
— 3096
2 025 904
2032Х997=2025904
Примеры для самостоятельного решения:
1) 10 031X9999= 4) 990X4354 =
2 3024X998= 5) 981X1003=
3) 99988X100012= 6) 10 101X9909=
ответы для проверки: 1) 100299969; 2) 3017952;
3) 9999999856; 4) 4310460; 5) 983943; 6) 100090809.
Умножение чисел, близких к 10_п. Поскольку все из-
ложенное в предыдущих разделах остается в силе и при
отрицательном значении п (а также при п, равном ну-
лю), метод дополнений представляет исключительную
ценность для инженеров, занимающихся расчетом на-
дежности элементов и систем, где приходится перемно-
жать десятичные дроби, очень близкие к единице (случай
п=0). Рассмотрим общий случай умножения десятич-
ных дробей, близких к 10-п.
Для того чтобы перемножить две десятичные дроби
(например, 0,0997X0,099), близкие к 10-п (в нашем слу-
чае близкие к 0,1, т. е. п= — 1), необходимо:
1) каждый из сомножителей умножить на 10м, где
т — число знаков после запятой сомножителя, имеюще-
го большее число десятичных знаков:
в числе 0,0997 — четыре знака;
в числе 0,099 — три знака,
следовательно, м=4
0,0997X10 000=997,
0,099X10 000=990;
2) перемножить получившиеся целые числа
997X990= 1000—997=3,
1000—990=10,
990—3=987,
3х10=30,
997X990=987 030;
3) отделить запятой в получившемся произведении
2мзнаков
| 0,0997X0,99=0,009 870 30.
В данном случае отделяем 2X4=8 знаков. Нуль в конце
I произведения, вполне естественно, можно не писать.
Метод получения произведения остался без измене-
ний. Первый и третий пункты призваны дать способ на-
хождения числа разрядов после запятой в окончательном
результате. Тот же способ перемножения можно описать
и несколько по-другому.
Пусть необходимо перемножить числа
0,00998X0,0098 =
1) выравниваем число знаков после запятой дописы-
ванием в одном из сомножителей необходимого числа
нулей:
0,00998X0,00980=
2) перемножаем сомножители как целые числа, не
обращая внимания на нули, стоящие перед значащими
цифрами,
998X980=
1000—998 = 2
1000—980=20
998—20=978
2X20=40
998—980=978 040
3) в окончательном результате отделяем запятой чис-
ло цифр, равное сумме числа цифр после запятой в обо-
их сомножителях после выравнивания
0,00998 X 0,00980=0,0000978040.
Примеры для закрепления материала:
0,981X0,999=
1) м=3, выравнивания не требуется,
2) 981X999=980 019 (см. с. 38),
3) 0,981X0,999 = 0,980019,
99,98X99,97=
1) м=2,
2) 9998X9997=99 950 006,
3) 99,98X99,97=9995,0006.
1,003X1,0022=
1) м = 4, 1,0030X1,0022 =
2) 10 030X10 022=100 520 660 (см. с. 39),
3) 1,003X1,0022=1,00520660.
0,00972=
1) м=4,
2) 972=9409 (см. с. 37),
3) 0,00972=0,00009409.
Решите самостоятельно:
1) 1,09X0,998= 4) 99,95X99=
2) 0,00997X0,0099= 5) 0,102X0,099=
3) 0,0989Х0,0995= 6) 0,011X0,0098=
ответы для проверки: 1) 1,08782; 2) 0,000098703;
3)0,00984055; 4) 9895,05; 5) 0,010098; 6) 0,0001078.
умножение чисел, близких к 2*10п (т. е. к 20, 200,
2000 и т. д.). Чтобы перемножить два числа, близких к
2-10п (например, 198X196, где п=2), необходимо:
1) найти дополнение каждого из сомножителей до
2-10п
200—198 = 2,
200—196 = 4;
2) из одного из сомножителей вычесть дополнение
второго сомножителя до 2- 10п
198—4= 196—2= 194;
3) полученный результат умножить на 2
194X2 = 388;
4) найти произведение дополнений
2X4=8;
5) к произведению, полученному в пункте 3, приписы-
ваем произведение дополнений, следя за тем, чтобы это
произведение занимало п разрядов,
198X196=38 808.
При практическом счете нет надобности в таком мелком
дроблении операций и задача сводится к следующему:
199X197=
Записываем удвоенную разность одного из сомножителей
и дополнение второго сомножителя до 2-10п
(199—3)Х2 = 392.
К полученному числу приписываем произведение допол-
нений
199X197=39 203.
Для того чтобы можно было использовать все частные
случаи метода, описанные на с. 36—44, дадим строгую
общую формулировку.
Чтобы умножить два числа, близких к 2-10п (напри-
мер 199,99-200,1), необходимо:
1) если сомножители имеют десятичные знаки, вырав-
нять число десятичных знаков, в каждом числе дописав
нули в одном из сомножителей:
199,99X200,10
дальнейшие вычисления производим, не обращая вни-
мания на запятую);
2) находим дополнение каждого из сомножителей до
2- 10п
20 000—19 999 = 1,
20 000—20 010=—10;
3) из одного из сомножителей вычитаем дополнение
другого сомножителя до 2*10п
19 999—(—10) =20 009 или 20 010—1=20 009;
4) полученный результат умножаем на 2*10п
20 009X20 000=400 180 000;
5) находим произведение дополнений
— 10X1=—10;
6) к результату, полученному в пункте 4, алгебраи-
чески прибавляем произведение дополнений
400 180 000—10=400 179 990;
7) в полученном результате (пункт 6) отделяем запя-
той число знаков, равное сумме числа знаков после за-
пятой в каждом из сомножителей (после выравнива-
ния), — см. пункт 1.
199,99X200,10=40017,9990.
В приводимых ниже примерах номера операций
соответствуют указанным выше, но, будем надеяться
вычисления будут ясны:
1988X1997= 1) 1988—3=1985,
12 3 2) 1985X2 = 3970,
3) 12X3 = 036 (записываем с учетом чис-
ла разрядов, которое должно занимать
произведение дополнений),
4) 1998X1997 = 3 970 036.
2017X1998= 1) 2017—2=1998— (—17) =2015,
—17 2 2) 2015X2000-4 030 000,
3) (__ 17)Х2=___ 34
4) 2017X1998=4 030 000—34 = 4 02996
Обоснование метода.
Пусть х=2*10п —ах, у = 2*10п —ау(ах и ау могут
быть Как положительными, так и отрицательными чис-
лами); тогда х*у= (2- 10п—ах) * (2- 10п—ау) =4*
*102п—2*10п*ах—2*10п *ау+ах*ау= (2*10п—ах—аУ)*2*
*10п+ах*ау.
Примеры для самостоятельного решения:
1) 209X211= 4) 0,021X0,0199 =
2) 179X199= 5) 0,19X0,19 =
3) 2011X1997= 6) 0,00201X0,00203=
Ответы для проверки: 1) 44 099; 2) 35 621; 3) 4015967
4) 0,0004179; 5) 0,0361; 6) 0,0000040803.
Умножение чисел, близких к 5*10п (т. е. близких к
50, 500, 5000 и т. д.). Метод дополнений дает хорошие
результаты и при применении его для умножения чисел,
близких к 5*10п.
Для того чтобы получить произведение двух чисел,
близких к 5*10п (например, 48X47, где п= 1), необхо-
димо:
1) найти дополнение каждого из сомножителей до
5*10п (в конкретном случае до 50)
50—48 =-2,
50—47=3;
2) из одного из сомножителей вычесть дополнение
другого
48—3=47—2=45;
3) к полученному результату приписать столько ну-
лей, сколько цифр в каждом из сомножителей, и затем
полученное число поделить на 2
4500:2=2250.
Другая формулировка этого пункта: полученный резуль-
тат умножить на 10п+1 и поделить на 2
45*102:2=2250;
(или полученный результат умножить на 5*10п
45X50 = 2250);
4) найти произведение дополнений
2X3=6;
5) к полученному в пункте 3 результату алгебраиче-
ски прибавить произведение дополнений
48X47=2250+6=2256.
Рассмотрим данный метод на нескольких примерах:
499X496=
1) 500—499=1,
500-495=5,
2) 495—1=494,
3) 494 000:2 = 247 000,
4) 5X1-5,
5) 499Х495=247 000+5=247 005.
503X505=
1) 500-503= -3,
500-505= -5
2) 503-(-5)=-5,
3) 508 000:2 = 254 000,
4) (-3)* (-5) = 15,
5) 503*505=254 000+15=254 015.
 501X498 =
501X498 =
1) 500—501 =—1,
500—498 = 2,
2) 501—2 = 499,
3) 499 000:2 = 249 500,
4) - 1*2 = - 2
5) 501X498 = 249 500—2 = 249 498.
0,504X0,511 =
Умножая каждый сомножитель на 103,
сводим пример к виду 504X511.
1) 500—504 = —4,
500—511=—11,
2) 511 — (—4) =515,
3) 515 000:2 = 257 500,
4) (- 4)*(- 11) =55,
5) 504X511=257 500+55 = 257 555,
6) 0,504X0,511=0,257555 (отделяем запятой 6 зна-I
ков, так как первоначально мы каждый из сомножи-
лей умножили на 1000, а все произведение увеличили в
1000 000 раз). После освоения метода можно рекомен-
довать следующий порядок вычислений. Для перемно-
жения чисел 58X57 необходимо:
1) разность одного из сомножителей и дополнение
второго сомножителя поделить на 2
58— (—7): 2=65: 2 = 32,5
(запятая потребовалась только для того, чтобы при за-
писи не нарушилось формальное равенство);
2) к полученному равенству приписываем произведе-
ние дополнений (если это произведение положительно
помня, что оно должно занимать столько разряддов
сколько их в каждом сомножителе (в случае, если ре-
зультат вычислений пункта 1 число целое), или на 1 раз-
ряд меньше, если результат — число дробное. В послед-
нем случае может возникнуть необходимость произвевести
соответствующее сложение:
325
+ 56
3306
58X57=3306.
Обоснование метода. 48
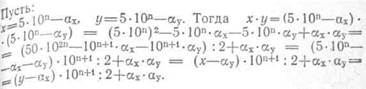
Примеры для самостоятельного решения:
1) 5003X4993= 4) 0,497X0,497=
2) 4999X4999= 5) 49989X49991 =
3) 0,5088X0,5004= 6) 0,049X0,053 =
Ответы для проверки: 1) 24 979 979; 2) 24 990 001;
3) 0,25460352; 4) 0,247009; 5) 2 499 000 099; 6) 0,002597.
Перемножение чисел, близких к а*10а (где а — одно-
значное число). Сформулируем результаты, полученные
ранее для общего случая. Чтобы перемножить два чис-
ла, близких к а * 10п (например, 402X401, где а=4, п =
=2), необходимо:
1) найти дополнение каждого сомножителя до а- 10*
(в нашем случае до 400)
400—402 = —2,
400—401 = —1;
2) из одного из сомножителей вычесть дополнение
Другого сомножителя
402—(—1) =403;
3) полученную разность умножить на а-10п (т. е. на
400)
403X400=161200;
4) к результату, полученному в пункте 3, прибавить
(алгебраически) произведение дополнений
(-2)Х(-1)=2,
402X401 = 161 200+2=161 202.
Практически проще выполнять вычисления по данно-
алгоритму в другой последовательности.
.Необходимо умножить 51X54= (а = 5, п=1):
находим произведение дополнений — результат
дает нам низшие разряды произведения. Записываем его
(—1)Х(—4)=4
51Х54 =...4.
Следим, чтобы произведение занимало празрядов (в
нашем случае п=1 и произведение занимает 1 разряд)
Если произведение занимает менее п разрядов, то недо-
стающие разряды заполняем нулями, например, если
произведение дополнений равно 12, а п= 3, то результат
запишем так:...012. Если произведение занимает боль
ше разрядов, чем п, то значение старшего разряда запо-
минаем. Например, произведение дополнений равно 15
п=1. В этом случае записываем...5 (единицу запоми-
наем);
2) к одному из сомножителей прибавляем единицы
другого сомножителя (если второй сомножитель больше,
чем а-10п) или вычитаем дополнение другого сомножи-
теля (если второй сомножитель меньше, чем а• 10п):
51+4 = 54+1 = 55;
3) умножаем полученное число на число десятков
(а) и записываем последовательно получающееся произ-
ведение перед записанным уже произведением единиц,
не забывая в случае необходимости учесть запомненное
число десятков, получившееся при нахождении произве-
дения дополнений,
51Х54=2754.
Основное преимущество данного алгоритма в том, что
можно сразу записывать окончательный результат. Про-
верьте на следующих примерах, насколько вы освоили
описанный метод:
81X83= 1) 83— (—1) =81 — (—3) =84,
— 1—3 2) 84X8=672,
3) (-1)Х(-3)=3,
4) 81X83 = 6723.
79X78= 1) 79—2 = 78—1=77,
1 2 2) 77X8 = 616,
3) 2X1=2
4) 79X78 = 6162.
28X25= 1) 28—5 = 25—2 = 23,
2 6 2) 23X3 = 69,
3) 2X5=10,
4) 28X25 = 690+10 = 700.
41Х39= 1) 41 —1=39(—1)=40,
- 1 1 2) 40X4=160,
3) 1Х(—1)= —1,
4) 41X39=1600—1 = 1599.
(в этом случае поступаем по основному алгоритму).
Обоснование метода.
Пусть х=а* 10п+в, у=а-10п +су тогда х*у=
=(а*10п+в)*(а*10п+с) = (а*10п+в+с)*а*10п+в*с=
= (у+в) * а* 10п+в*с= (х+с) *а* 10п+в*с.
Примеры для самостоятельного решения:
1) 69X69= 4) 5,01X5,08=
2 3007X3003= 5) 27X29 =
3) 509X504= 6) 31X28 =
Ответы для проверки: 1) 4761; 2) 9 030 021; 3) 256 536;
.4) 25,4508; 5) 783; 6) 868.
Умножение чисел разного порядка, близких к 10п,
2- 10п, 5 • 10п. После изучения материала, изложенного выше, легко освоить и случай, когда сомножители имеют
разные порядки. Приводимые примеры не требуют до-
полнительных пояснений.
993X98 = 993X980: 10=
7 20
1) 993—20 = 980—7 = 973,
2) 20X7=140,
3) 993X980 = 973140,
4) 993X98 = 97314.
1008X109=1008X1090: 10
—8 —90
1) 1008—(—90) = 1090—(—8) = 1098,
2) (-8) X (-90) =720,
3) 1008X1090=1098 720,
4) 1008X109 = 109 872.
10009X99 = 10009X9900: 100=
-9 100
1) 10009—100 = 9900— (—9) -9909,
2) (-9) XI00 = —900,
3) 10 009X9900=9909X10 000—900=
=99 089 100,
4) 10 009X99 = 990 891.
202Х2002 = 2020X2002:10—
—20 —2
1) 2020— (—2) = 2002— (—20) = 2022,
2) (-20) X (-2) =40,
3) 2020X2002 = 4 044 000+40 = 4 044 040,
4) 202Х2002 = 404 404.
Необходимо отметить, что не всегда целесообрано
пользоваться сокращенными приемами умножения,на-
пример, последний пример, наверно, проще решить, про-
делав умножение столбиком в уме.
199X19=199X190=
1 10
1) 199—10=190—1 = 189,
2) 189X100X2 = 37 800,
3) 10X1 = 10,
4) 199X190=37 800+10 = 37 810,
5) 199X19=3781.
23X197 = 230X197: 10=
—30 3
1) 230—3=197—(—30) =227,
2) 227X100X2 = 45 400,
3) (-30)ХЗ = -90,
"4) 230X197=45 400—90 = 45 310,
5) 23X197=4531.
52X508 = 520X508: 10 =
—20 —8
1) 520— (—8) = 508— (—20) = 528,
2) 528X1000:2 = 264 000,
3) (-20) X (-8) = 160,
4) 520X508 = 264 000+160 = 264 160,
5) 52X508 = 26416.
49X4991=4900X4991: 100 =
100 9
1) 4900—9 = 4991 — 100 = 4891,
2) 4891X10 000:2 = 24 455 000,
3) 100X9 = 900,
4) 4900X4991=24 455 000+900 =
= 24 455 900,
5) 49X4991=244 559.
Примеры для самостоятельного решения:
1) 999X99= 10) 99 975X97=
2) 10 007X1007= 11) 9931X100 003=
3) 10 031X99= 12) 997X99 998=
4) 591X51= 13) 50,01X500,2=
5) 0,495X49,999= 14) 5,09X50,9 =
6) 511X4996= 15) 4988X498 =
7) 1,999X20,003= 16) 2,0034X19 =
8) 1,996X0,0199= 17) 19X198 =
9) 1981X191= 18) 0,0211X0,19=
Ответы для проверки:.1) 98901; 2) 10077 049; 3) 993069;
4) 30141; 5) 24,749505; 6) 2552956; 7) 39,985997;
8) 0 0397204; 9) 378 371; 10) 9 697 575; 11) 993 129 793;
12) 99 698 006; 13) 25015,002; 14) 259,081; 15) 2 484 024;
16) 38,0646; 17) 3762; 18) 0,004009.
Умножение двузначных чисел на двузначные, десят-
ки которых не равны, можно свести к основному случаю,
писанному выше, если вспомнить, что дополнения мо-
гут быть по абсолютной величине и больше десяти:
82X61
—22 —1
За а принимаем число десятков меньшего числа (а=6):
1) (-22)Х(~1)=22
82X61 =-...22 (2 запоминаем),
2) 82—(—1) =83,
3) 83X60=4980,
4) 82X61=4980+22 = 5002.
Такой способ нахождения произведения пригоден для
любых двузначных чисел, но наиболее эффективен он
тогда, когда: а) число десятков меньшего сомножителя
мало; б) число единиц мало в обоих сомножителях (или
хотя бы в одном из сомножителей).
22X53 =
-2 -33
1) (-2)X(-33) =66,
22X53=...б6 (6 запоминаем)
2) 53—(—2) =55,
3) 55X20=1100,
4) 22X53=1166.
62Х52=
-12 —2
1) (-12)X(-2) =24.
62X52 =...24,
2) 62—(—2) =64,
3) 64X50 = 3200,
4) 62X52 = 3224.
Не менее эффективен способ, когда число единиц в
обоих сомножителях (или в одном из них) близко к 10.
В том случае часто выгодно принять за а число десят-
ков большего сомножителя, увеличенное на 1.
27*39 1) 13X1=13 (а=4),
13* 1 2) 39—13 = 26,
3) 26X40=1040,
4) 27X39= 1040+13= 1053.
59X69= 1) 11Х1 = 11 (а=7),
11 1 2) 59—1=58,
3) 58X70 = 4060,
4) 59X69 = 4071.
Если число единиц большего сомножителя мало, а число
единиц меньшего сомножителя велико, то за а-10 целого
сообразно брать число, большее, чем меньший сомножи-
тель, и меньшее, чем больший сомножитель.
61Х49 = за а*10 берем 50.
— 11 1 1) (—11)Х1= —11.
2) 61 — 1 = 60,
3) 60X50 = 3000,
4) 61X49 = 3000—11=2989
72X49 за а-10 берем 50.
—22 1 1) 72—1 = 71,
2) 71X50=3550,
3) (-22)Х1=-22,
4) 72X49 = 3550—22 = 3528
Примеры для самостоятельного решения:
1) 29X49= 3) 43X29= 5) 69X49=
2) 31X52= 4) 71Х8т= 6) 23X43 =
Ответы для проверки: 1) 1421; 2) 1612; 3) 1240; 4) 57
5) 3381; 6) 989.
Распространение метода на случай нахождения про-
изведения трех сомножителей. Для того чтобы найти
произведение трех сомножителей, близких к 100,
97X98X99
необходимо:
1) найти дополнение каждого множителя до 100
97X98X99;
3 2 1
2) из одного из сомножителей вычесть сумму допол
нений двух других сомножителей
97—2—1 =98—3—1 =99—3-Я = 94,
получечная разность дает первые две цифры окончатель
ного результата
97X98X99 = 94...;
3) найти сумму попарных произведений дополнений
3X2+3X1+2X1 = 11;
результат, уменьшенный на единицу (11 —1 = 10), дает
следующие две цифры окончательного результата:
97X98X99 = 9410...
(еслй сумма произведений будет больше 99, то число со-
тен прибавляется к последней цифре результата преды-
дущего пункта.)
4) перемножить дополнения и найти дополнение по-
ученного произведения до 100
3X2X1=6,
100—6=94,
полученный результат дает последние две цифры окон-
чательного результата
97X98X99 = 941 094.
Если произведение дополнений дает трехзначное число,
то число сотен надо вычесть из последней цифры окон-
чательного результата, полученного в пункте 3.
Рассмотрим нахождение произведения в общем виде.
Пусть необходимо произвести умножение трех чисел х,
у и z, причем каждое из них близко к 10п: х:=10п—а,
у=10п—b, z =10п— с:х*у*z=(10п—а) * (10п—b) *(10п—
*c) = Ю3п—102п (а+b+с) + 10п (а*b+b*с+с*а) — а*Ь*
*c= (10п— а—b— с) • 102п + (а*b + b*с+с*а)*10п+(10п
—а*b*с).
Из полученного результата видно, что первые п цифр
.получаются путем вычитания из любого сомножителя
дополнении двух других сомножителей, следующие п
цифр — путем нахождения суммы произведений допол-
нений (уменьшенной на единицу) и, наконец, последние
п цифр — дополнение произведения а-b-с до 10п.
Пример: 995X997X991 =
5 3 9
1) 995 - 3 -9 = 983
2) 5X3+5X9+3X9=87 (в окончательный
результат запишется
087)
3) 5X3X9=135,
4) 983 087 000—135 = 983 086 865.
R такому же результату мы придем, если будем действо-
вать так, как описано при умножении чисел, близких
100:
1) 995—3—5=983,
2) 5X3+5X9+3X9 = 87, 87—1=086,
3) 5X3X9=135,
4) 1000—135 = 865,
5) 995X997X991=983 086 865.
Используя общую формулировку, легко понять, ка-
кие необходимо производить действия для умножения
чисел, больших 10п.
Приведем пример:
1003X1004X1007 =
—3 —4 —7
1) 1003+4+7=1014,
2) (-3) • (-4) + (-4) • (-7) + (-3) • (-7)=
=61 (в результат запишется 061)
3) 3X4X7=84 (в результат запишется 0841
4) 1003X1004X1007=1014 061084.
Аналогично находятся произведения, когда один или два
сомножителя имеют дополнения другого знака, чем тре-
тий сомножитель. Достаточно в приведенной выше фор-
муле учесть знаки дополнений.
Примеры для самостоятельного решения:
1) 12X14X15= 3) 103Х 99X101= 5) 999X997X996=
2) 95X99X98= 4) 103X110X105=6) 997X995X1003=
Ответы для проверки: 1) 2520; 2) 921690; 3) 1029897
4) 1 189 650; 5) 992 018 988; 6) 994 991045.
Необходимо заметить, что прием эффективен только
в случае, если все сомножители близки к 10п. Если отли-
чие хотя бы у одного сомножителя от 10п существенно,
то расчеты становятся достаточно громоздкими для уст-
ных вычислений.
Читатель может самостоятельно рассмотреть умно-
жение трех сомножителей, близких к 5*10п или к 2*10п.
Получающиеся при этом формулы требуют определенно-
го навыка для использования их при устных вычислени-
ях и поэтому здесь не приводятся.
7. УМНОЖЕНИЕ НА ЧИСЛО, БЛИЗКОЕ К 10п
Умножение двузначного числа на число, близкое
к 100. Чтобы умножить произвольное двузначное число
(например, 66) на число, близкое к 100 (например, 98),
необходимо:
1) от числа отнять дополнение второго множителя до
100
66—(100—98) =64.
Результат дает число сотен окончательного результата
66X98 = 64...;
2) найти дополнение первого числа до 100
100—66=34;
3) умножить полученное дополнение на дополнение
второго числа до 100
34X2=68;
4) к результату, полученному в пункте 1, приписыва-
ем результат, полученный в предыдущем пункте, следя
за тем, чтобы он занимал два разряда,
66X98=6468.
Если произведение дополнений является числом
трехзначным, то число сотен произведения складывается
с числом сотен, полученных в пункте 1. Например:
66X97= 1) 100—97=3,
66—3 = 63,
2) 100—66=34,
3) 34X3=102,
4) 66X97 = 63
+ 102
6402
Несколько поясняющих примеров:
83X98= 1) 100—98 = 2, 39X95= 1) 100—95 = 5,
83—2 = 81, 39—5=34,
2) 100—83=17, 2) 100—39 = 61,
3)17X2=34, 3) 61X5=305,
4)83X98 = 8134. 4) 39X95 = 34
+305
3705
Проделайте самостоятельно следующие вычисления:
1) 58X97= 3) 75X95= 5) 92X97=
2) 29X98= 4) 88X94= 6) 87X89 =
Ответы для проверки: 1)5626; 2) 2842; 3) 7125; 4) 8272;
5) 8924; 6) 7743.
Умножение многозначного числа на число, близкое к
100. Чтобы многозначное число умножить на число,
близкое к 100 (например, 452X98), необходимо:
1) найти разность между множимым и произведени-
ем числа сотен множимого, увеличенного на единицу
(4+1= 5), на дополнение множителя до 100 (100—
-98=2)
452-(5Х2)=442.
2) К полученному числу надо приписать произведе-
ние дополнения до 100 числа, образованного последними
двумя цифрами множимого (100 —52 = 48), на дополне-
ние множителя (100—98=2)
48X2=96,
452X98 = 44 296.
Пример на применение метода:
289X97=
1) находим произведение числа сотен множимого
увеличенного на единицу, и дополнения множителя до
100
(2+1) X (100—97) =9;
2) из множимого вычитаем полученное произведение
289—9 =280;
3) находим дополнение до 100 числа, образованного
последними двумя цифрами множимого
100—89=11;
4) произведение дополнений множимого и множителя
дают последние две цифры окончательного результата
11X3=33.
Итак, 289X97 = 28 033.
Более математически точно данный метод надо сфор-
мулировать так: при умножении целого числа на число,
близкое к 100, число сотен произведения находится как
разность между множимым и произведением числа его
сотен, увеличенного на единицу, на дополнение множи-
теля до 100. Произведение дополнений числа, образован-
ного последними двумя -цифрами множимого и множи-
теля до 100, дает число единиц окончательного резуль-
тата.
Уточнение второй формулировки заключается в том,
что при нахождении произведения дополнений части
множимого и множителя иногда может получаться и
трехзначное число. В этом случае число сотен этого про-
изведения надо сложить с последней цифрой разности,
полученной при нахождении числа сотен окончательного
произведения («приписывание» справедливо только
том случае, если произведение дополнений дает двузнач-
ное число).
341X98= 1) (3+1)Х(100—98) =8,
2) 341—8 = 333,
3) 100—41=59,
4) 59X2= 118,
5) 341X98 = 333X100+118 = 33 418.
899X98= 1) (84-0X2= 18,
2)899—18 — 881,
3) 100—99=1,
4) 1X2 = 2,
5) 899X97 = 88 102.
Обратите внимание на то, что в примере 899X97 =
число разрядов, отводимое под произведение дополнений,
равно двум.
Метод умножения не столь сложен, как это может
показаться с первого взгляда, а для освоивших метод
дополнений (пункт 6) вообще не представляет затрудне-
ний, так как является его развитием или повторением.
Доказательство правильности метода.
Пусть множимое равно (100а+10Ь+с), а множи-
тель—100— х, где х — дополнение множителя до 100.
Составляем выражение согласно приведенному правилу
[(100а+10Ь+с) + (а+1)]-100+(100— 10 Ь—с)*х.
Раскрывая скобки и приводя подобные члены, убеж-
даемся, что получается тот же ответ, что и при раскры-
тии скобок выражения (100а+10Ь+с)Х(100— х).
Примеры для самостоятельного решения:
1) 851X96= 3) 2099X96= 5) 789X97 =
2) 75X98= 4) 391X97= 6) 69X98 =
Ответы для проверки: 1) 81696; 2) 7350; 3) 201504;
4) 37 927; 5) 76 533; 6) 6762.
Умножение на число, близкое к 10п. Поняв и освоив
способ умножения на число, близкое к 100, легко обоб-
щить метод для умножения на число, близкое к 10п. Хо-
тя при этом приходится оперировать с большими числа-
ми и метод становится малопригодным для устных вы-
числений, тем не менее его применение дает существен-
ное упрощение при письменных вычислениях.
При умножении м-значного числа на число, близкое
к 10п, число, образованное первыми (т—п) цифрами
Множимого, надо увеличить на единицу и умножить на
Дополнение множителя до 10п. Это произведение надо
учесть из множимого. К полученной разности, умно-
енной на 10п, необходимо прибавить произведение до-
°лнения до 10п числа, образованного последним п циф-
рами множимого, на дополнение множителя до 10п:
12789X998= (м=5,п=3),
1) число, образозанное первыми (т — п) цифрами
множимого увеличиваем на 1 и умножаем на дополне-
ние множителя
(12+1) X (1000—998) = 26;
 2) полученное произведение вычитаем из множимого
2) полученное произведение вычитаем из множимого
и разность умножаем на 103
(12 789—26) X 103= 12 763 000;
3) находим произведение дополнения до 10п (т. е. до
1000 в нашем случае) числа, образованного последними
3 цифрами множимого, на дополнение множителя
(1000—789) Х2 = 211X2 = 422;
окончательный результат
12 789X998=12 763 422.
Так же, как и в предыдущем случае, правильность ме -
тода доказывается составлением выражения согласно
описанному алгоритму и непосредственной проверкой
его раскрытием скобок.
Два примера на применение метода:
877X997= 1) (0+1)ХЗ = 3,
2) 877—3 = 874,
3) 1000—877=123,
4) 123X3 = 369,
5) 877X997 = 874 369.
54X998=- 1) (0+1)Х2 = 2,
2) 54—2 = 52,
3) 1000—54 = 946,
4) 946X2=1892,
5) 54X998=53 892.
Примеры для самостоятельного решения:
1) 973 129X9997= 4) 78X9997=
2) 159X996= 5) 6666X996 =
3) 3443X9998= 6) 359X999 =
Ответы для проверки: 1) 97 228 370 613; 2) 158 364;
3) 34 423 114; 4) 779 766; 5) 6 639 336; 6) 358 641.
8. УМНОЖЕНИЕ НА ЧИСЛО ВИДА 9, 99, 999,... 10"—1
Умножение на 9 однозначных чисел. Приводимый ни-
же способ может существенно облегчить изучение (вер
нее, запоминание) последнего столбика таблицы умно-
жения, а именно — умножения однозначных чисел на *
Предположим, необходимо перемножить
4X9.
Положим на стол рядом обе руки с вытянутыми пальца
ми. Приподнимем соответствующий палец, обозначаю-
щий множимое (считая с левой стороны