Метод Фурье. Истории известно около 30 общих спо
собов умножения, отличающихся один от другого либо схемой записи, либо самим ходом вычисления. Из этих способов, как справедливо отмечает Л. С. Каган в раоб-те «Устный счет и рационализация вычислений», обычный, принятый у нас, является наиболее удобным для школьного преподавания в младших классах, но отнюдь не наиболее рациональным на практике. Следует настоятельно рекомендовать освоить тот способ умножения,который индусы называли молниеносным, а греки— хиазм.
Итальянцы его называют рег сrосеttа, т. е. накрест. Со
ветскому читателю он более известен как метод Фурье
хотя в начале века после блестящих выступлений в Ро
сии знаменитого счетчика Ферроля он обычно называл-
ся способом умножения Ферроля.
Рассмотрим суть метода на примере умножения двух
трехзначных чисел
* 123X214.
1) Единицы произведения получаем, перемножая еди-
ницы сомножителей

2) Десятки найдем, сложив произведения десятков
каждого множителя на единицы другого множителя
(2X4+3X1) = 11,
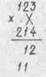
3) Сотни получаются как сумма следующих произве-
дений: сотен одного сомножителя на единицы другого
сомножителя, сотен второго сомножителя на единицы
первого сомножителя, десятков одного сомножителя
на десятки второго сомножителя: 1X4+2X3 + 2X1 = 12

4) Тысячи получаются сложением произведений со-
тен на десятки и десятков на сотни 1X1+2X2 = 5;

5) Десятки тысяч получаются умножением сотен на

|
Окончательный результат

|
Способ прост благодаря тому, что легко запомнить
графическую схему последовательности выполнения вы-
числений, которая является симметричной:

Если на каком-либо шаге получаем двузначное число, то
записываем только единицы суммы, а десятки запоми-
наем и учитываем при вычислении следующего разряда.
Выполним умножения по данной схеме без дополни-
тельных пояснений:


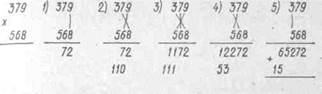
215272
Выполняя вычисления шаг за шагом, надо всегда
помнить, что на первом шаге вычислений мы получаем
первую правую цифру окончательного результата, на
втором шаге — вторую цифру окончательного результа-
та и т. д. В противном случае (смотри последний при-
мер, где суммы получаются трехзначные) легко сбиться
и попасть не в те разряды, которые следует.
При нахождении произведения с применением данно-
го метода наиболее сложным является третий шаг, где
в уме надо находить и запоминать три произведения.
Рекомендуем следующую последовательность вычисле-
ний;
579
Ж
568
(последовательность нахождения произведений произ-
вольная, какая вам больше нравится): 1) 3-8 = 24,
2) 5-9 = 45, 3) 24+45 = 69, 4) 6*7 = 42, 5) 69+42=111.
Суть рекомендации сводится к тому, чтобы запоминать
не более двух чисел, найдя два произведения -- сложить
их, и затем, запоминая только одно число (сумму), про-
должать вычисление.
На первых порах, может быть, будет даже целесооб-
разно выполнять вычисления этого шага письменно.
Описанный выше метод справедлив и при умножении
чисел разной разрядности. Для того чтобы умножить
трехзначное число на двузначное, достаточно предста-
вить мысленно двузначное число как трехзначное:
242 представим как 242
Х 54 Х054
Теперь к данному примеру полностью применим метод
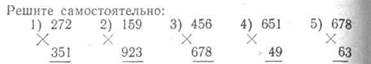
|
 Ответы для проверки: 1) 95472; 2) 146 757; 3) 309168*
Ответы для проверки: 1) 95472; 2) 146 757; 3) 309168*
4) 31899; 5) 42 714.
Доказательство правильности метода проще всего
провести, выполнив обычным способом умножение чисел
в общем виде. Обозначим трехзначное число 100а+

складывая, окончательный результат запишем в строчку:

Теперь остается только внимательно посмотреть на по-
лученный результат и убедиться, что, используя пред-
лагаемый метод, мы не отклонились от классической
схемы умножения «столбиком». Этот же метод дает от-
личные результаты и при умножении двузначных чисел
на двузначные.

Например:

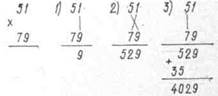
|
 Общий метод сокращенного умножения многозначных
Общий метод сокращенного умножения многозначных
чисел. При необходимости умножить многозначное число
на число той же значности можно рекомендовать следую-
щий метод, который опишем на примере умножения чи-
сел
*261
1) Производим умножение цифр, стоящих друг под
другом;

Обратим внимание на то, что для записи каждого произ-
ведения отводится 2 разряда.
2) Производим умножение накрест соседних цифр.
Результат пишем под результатом первого шага со сдви-
гом на 1 знак влево

(5*1+4*6=29; 2*5+3*6=28)
3) Умножаем накрест крайние цифры и их сумму за-
сываем под результатом второго шага со сдвигом
на 1 знак влево

|
(3. 1+2-4=11)
Схема, по которой ведется расчет, очень легко запоми-|
нается
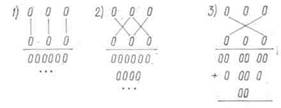
В случае умножения четырехзначных чисел на четы-
рехзначные схема приобретает следующий вид:

Из приведенной схемы легко вывести алгоритм для
вычисления произведения двух чисел произвольной знач-
ности: первый шаг — перемножение цифр, стоящих друг
под другом, второй и остальные шаги вычислений дела-
ются по общей схеме —сначала перемножаются накрест
рядом стоящие цифры, затем перемножаются накрест
цифры, отстоящие друг от друга на одну цифру, затем
отстоящие друг от друга на две цифры, и т. д.
В каждом шаге, начиная со второго, надо найти ряд
сумм, каждая из которых состоит из двух слагаемый
где слагаемое —произведение двух цифр. Для записи
каждой суммы отводитсл 2 разряда (если сумма полу-
чается трехзначной, старший разряд суммы запоминает-
ся и прибавляется к последующей сумме слева). Каждая
последовательность записей следующего шага записыва-
ется со сдвигом влево на 1 разряд по сравнению с пре-
дыдущим шагом. Если в множителях различное число
знаков, то меньшее число рассматриваем как число, у
которого старшие разряды равны нулю.
X
2742
377
рассматриваем как
2742
Х0377
Это дает возможность умножать с помощью данного при-
ема числа с различным числом разрядов.
Рассмотрим два примера на использование метода:


Решите самостоятельно следующие примеры, используй
описанный метод:
1) у391 2) 1243 3) 28 4) 455 5) 4455
Х458Х3564 Х67 Х 634 Х 634
Ответы для проверки: 1) 179 078; 2) 4 430 052; 3) 1876-
4) 288 470; 5) 2 824 470.
Доказательство метода аналогично доказательству,
приведенному в предыдущем пункте.
Метод сдвига. К общим методам, упрощающим вы-
числение произведений чисел произвольной значности,
относится и метод сдвига, который является разновид-
ностью метода, изложенного выше.
Рассмотрим применение метода на конкретном при-
мере
362
Х 145
Запишем второй множитель в обратном порядке
541
Ниже запишем первый множитель так, чтобы число еди-
ниц первого множителя стояло под цифрой сотен второ-
го множителя (в обратной его записи)
541
1
362
1) перемножим цифры, стоящие друг под другом. По-
лучим единицы окончательного результата. Если число
двузначное — десятки запомним:
541
1
362
'0
2) мысленно сдвинем влево первый множитель на
1 знак. Стоящие друг под другом цифры перемножим и
произведения сложим. Сумма (с учетом запомненного
числа) даст нам десятки окончательного результата:
11 2X4+5x6 = 38, 38+1=39
3 62
390
Каждый последующий шаг будет заключаться в сдвиге
верхнего множителя влево на один разряд, нахождении
произведений стоящих друг под другом цифр и нахож-
дений этих произведений суммы, единицы которой за-
писываются в окончательный результат.
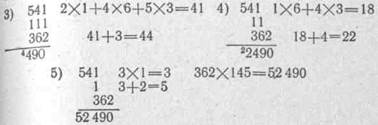
При использовании метода не забудьте, что один из
сомножителей должен быть записан в обратном порядке.
Числа должны быть записаны так, чтобы единицы чисел,
которые необходимо перемножить, были подписаны друг
под другом.
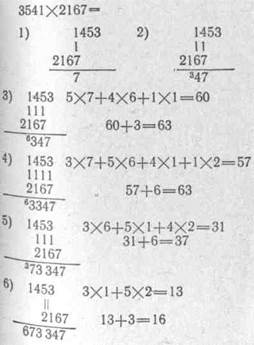
|
4X7+6X1=34
7) 1453 3X2 = 6 6+1=7 3541X2167 = 7 673 347
2167
7 673 347
Метод применим для умножения чисел любой знач.
ности и чисел, имеющих различное число разрядов.
Проделайте самостоятельно приводимые ниже вы-
числения, используя метод сдвига:
1) 315 2) 4258 3) 452 4) 43 5) 35 412
X X X X X
4274321 349 24 239
Ответы для проверки: 1) 134 505; 2) 18 398818-
3) 157 748; 4) 1032; 5) 8 463 468.
Доказательство правильности метода совпадает с
доказательством корректности предыдущих приемов!
(выполняем умножение двух чисел в общем виде стол-|
биком и затем убеждаемся в том, что слагаемые в обоих*
случаях одни и те же).
3. РУССКИЙ СПОСОБ УМНОЖЕНИЯ И ДЕЛЕНИЯ
(способ изменения сомножителей)
Изложение метода в общем виде. Если один из со]
множителей увеличить в т раз, а второй сомножитель
во столько же раз уменьшить, то произведение не изме-
нится. Этим свойством произведения можно пользовать-
ся для облегчения вычислений. Например:
25X24= (25X4) X (24:4) = 100X6=600,
13X18= (13Х6)Х(18:6) =78X3=234.
Прием дает хорошие результаты при умножении на
двузначные числа. Применяя его, очень часто удается
свести умножение на двузначное число к умножению на
однозначное число с последующим умножением опять
на однозначное число
23X15=115X3=345.
Активное усвоение метода заключается в том, чтобы
в каждом отдельном случае быстро сообразить, как мож-
но упростить множимое или множитель. При этом све-
дение к умножению на однозначное число — только част-
ный случай.
35X55= (34:2) X (55X2) = 17Х110.
Умножать на 11О проще, чем на 55.
умножение на число вида 5-10п. Способ изменения
сомножителей упрощает умножение на числа вида 5-1011.
Если необходимо умножить
246X5,
то,уменьшая первый множитель в 2 раза, а второй мно-
житель увеличивая в 2 раза, получим:
(246:2) X (5X2) = 123X10= 1230,
257X5=128,5X10=1285,
349X5=174,5X10=1745.
Отсюда вытекает правило: чтобы умножить число на
5 его необходимо умножить на 10 и разделить на 2
257X5 = 2570:2=1285,
349X5 = 3490:2=1745.
Аналогично происходит умножение на 5-10п.
7292X5-10П = 36 460-10п
273Х500=136,5Х10Х100=136 500
43X0,005=43X5-10-3=215-10~3=0,215.
Решите самостоятельно:
1) 397X50= 3) 12,54X500= 5) 18 500X0,005=*
2) 423X5-107= 4) 136,54X5-10-4= 6) 159X0,5 =
Ответы для проверки: 1) 19850; 2) 2115-107; 3) 6270;
4) 6827-10-5; 5) 92,5; 6) 79,5.
Умножение на 25 10п. Чтобы умножить число на 25,
его необходимо умножить на 100 и разделить на 4:
1232X25=123200:4 = 30 900
9532X25 = 953200:4 = 238 300.
Множитель 10±п не меняет алгоритма нахождения произ-
ведения:
378X25-104 = 37 800:4-104= 9600- 104 = 96-10б,
36X25-10-2=3600:4-10-2=900-10-2=9,
157X2500=15700:4-100 = 392 500.
Найдите самостоятельно:
1) 15 432X2500= 4) 297X0,25=»
2) 458X25-107= 5) 666X0,025 =
3) 236X25-10-2= 6) 1756Х25-102 =
Ответы для проверки: 1) 38580000; 2) 1145-Ю8; 3) 59;
4) 74,25; 5) 16,65; 6) 439-104.
Умножение на 125-10п. Чтобы умножить число на 125,
Не°бходимо это число умножить на 1000 и разделить на 8.
453X125 = 453 000:8 = 56 625,
129X125= 129 000:8= 16 150.
3- А- С. Сорокин 33
Так же, как и в предыдущих случаях, наличие множите-
ля 10±п не изменяет характера вычислений
354-0,125=354 000:8-10-3;
множитель 10±п проще учитывать на конечной стадии
числений.
Решите самостоятельно:
1) 1253X125-103= 4) 475X125- 10-2=
2) 459X12 500= 5) 707X125-104=
3) 174X0,0125= 6) 734X125000=
Ответы для проверки: 1) 156625-103; 2) 5737500-
3) 2,175; 4) 59 375-10"2; 5) 88375-104; 6) 91750 000. 3
Деление на 5 10п; 25-10п; 125-10п. Освоив умножение
на 5, 25, 125, легко перейти и к делению на эти числа.
Чтобы разделить число на 5, его надо умножить на 2 в
разделить на 10:
537:5= (537X2):10- 1074:10-107,4,
254:5= (254Х2):10= 508:10= 50,8.
Чтобы разделить число на 25, его надо умножить на 4 и
разделить на 100:
120:25-(120X4):100 = 4,8,
231:25= (231X4): 100-9,24.
Чтобы разделить число на 125, необходимо его умножить
на 8 и разделить на 1000:
6:125= (6X8):1000=0,048,
2431:125-(2431X8):1000= 19,448.
Наличие в делителе множителя вида 10±п не меняет
порядка вычислительного процесса. Множитель 10±п
проще всего учитывать в конечном результате, не забы-
вая, что при этом меняется знак у п:
231:(5-104)«=(231Х2):10*10-4=46,2-10-4=
= 462 -10-5 = 0,00462,
229: (25-10-3) = (229X4): 100*103 = 9160,
130:12 500= (130X8):1000-10-2= 104-10-4,
Выполните самостоятельно вычисления:
1) 293: (126-10-2)= 3) 6:(125-103) = 5) 712: (5- 10-3)=
2) 124:500= 4) 51:25= 6) 429:1,25=
Ответы для проверки: 1) 234,4; 2) 0,248; 3) 48; 4) 2,04
5) 142 400; 6) 343,2.