В пищевой промышленности в основном применяются приме прямозубые конические колеса, поэтому мы рассмотри расчет именно прямозубых конических колес.
В проектировочном расчете закрытых зубчатых передач определяем внешний делительный диаметр (конуса) приводного колеса по зависимости:
 (56)
(56)
где, Т2 - крутящий момент на валу ведомого зубчатого колеса, Нмм;
и - передаточное отношение зубчатых колес, которое принимается из рекомендованного ряда в соответствие с ГОСТ 12289-76 по табл. 32;
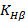 - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца колеса и определяется так же как и для цилиндрических зубчатых колес по табл. 22;
- коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца колеса и определяется так же как и для цилиндрических зубчатых колес по табл. 22;
[  ] - допускаемое контактное напряжение при проектировочном расчете определяется, так же как и для цилиндрических колес по зависимости (57):
] - допускаемое контактное напряжение при проектировочном расчете определяется, так же как и для цилиндрических колес по зависимости (57):
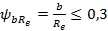 (57)
(57)
-коэффициент ширины зуба, который для проектных расчетов согласно ГОСТ 12289-76 принимается равным 0, 285;
 - длина зубьев, мм;
- длина зубьев, мм;
 - внешнее конусное расстояние, мм.
- внешнее конусное расстояние, мм.
Таблица 32.
| И | 1-й ряд | 1, 25 | 1, 60 | 2, 0 | 2, 50 | |
| 3, 15 | 4, 00 | 5, 00 | 6, 30 | |||
| 2-й ряд | 1, 12 | 1, 40 | 1, 80 | 2, 24 | 2, 80 | |
| 3, 55 | 4, 50 | 5, 60 |
Полученные расчетные значения диаметра округляют до значений рекомендованных ГОСТ 12289-76, приведенных в табл. 33.
Таблица 33.
| de2, | 1-й | |||||
| ММ | ряд | |||||
| 2-й | ||||||
| ряд |
Примечание: В таблицах 32 и 33 предпочтительным является применение первого ряда.
Определение чисел зубьев зубчатых колес:
Минимальное число зубьев малого (ведущего) колеса рекомендуется принимать в пределах  18... 32.
18... 32.
Число зубьев ведомого колеса определяем по зависимости:
 (58)
(58)
После определения чисел зубьев необходимо уточнить передаточное отношение по принятой в кинематическом расчете методике.
Определение внешнего окружного модуля зацепления по зависимости:
 [мм] (59)
[мм] (59)
где,  - внешний делительный диаметр, принятый по расчету и округленный до рекомендованного значения, мм. Полученное значение округлять не обязательно.
- внешний делительный диаметр, принятый по расчету и округленный до рекомендованного значения, мм. Полученное значение округлять не обязательно.
Определение параметров зубчатых колес, которые будут приведены в чертежах для их изготовления:
 (60)
(60)
- угол делительного конуса ведущего колеса
 (61)
(61)
- внешнее конусное расстояние
 (62)
(62)
- ширина зубчатого венца
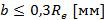 (63)
(63)
- среднее конусное расстояние
 (64)
(64)
- средний окружной модуль
 (65)
(65)
- внешняя высота зуба
 (66)
(66)
- внешняя высота головки зуба
 (67)
(67)
- внешняя высота ножки зуба
 (68)
(68)
- угол головки зуба
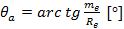 (69)
(69)
- угол ножки зуба
 (70)
(70)
- угол конуса вершин зубьев
 (71)
(71)
внешний диаметр вершин зубьев
 (72)
(72)
внешняя постоянная хорда в сечении, которое проходит нормально к зубу
 (73)
(73)
высота до внешней постоянной хорды
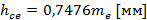 (74)
(74)
Проверка зубьев конических прямозубых колес на выносливость по напряжениям изгиба выполняют по следующей зависимости:
 (75)
(75)
где, KF - коэффициент нагрузки при расчете на изгиб, выбираемый так же, как и для расчета цилиндрических прямозубых колес;
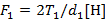 (76)
(76)
Т1 - крутящий момент на валу ведущего колеса, Нмм;
d1 - внешний делительный диаметр шестерни, мм;
YF — коэффициент формы зуба, выбираемый в зависимости от эквивалентного числа зубьев колеса по зависимости:
 (77)
(77)
принимается также как и для цилиндрических зубчатых колес;
 = 0,85 - опытный коэффициент, учитывающий понижение нагрузочной способности конических прямозубых колес по сравнению с цилиндрическими прямозубыми колесами;
= 0,85 - опытный коэффициент, учитывающий понижение нагрузочной способности конических прямозубых колес по сравнению с цилиндрическими прямозубыми колесами;
m - средний модуль зацепления, мм;
[  ] - допускаемое напряжение на изгиб выбирают точно так же как и для цилиндрических прямозубых колес.
] - допускаемое напряжение на изгиб выбирают точно так же как и для цилиндрических прямозубых колес.
В коническом прямозубом зацеплении возникают силы вызывающие или изгиб или кручение валов, где установлены шестерня и колесо. Эти силы определяются по зависимостям:
окружное усилие
 (78)
(78)
где, N - передаваемая мощность, кВт;
 - диаметр делительного конуса шестерни, мм;
- диаметр делительного конуса шестерни, мм;
 - частота вращения шестерни, мин-1;
- частота вращения шестерни, мин-1;
радиальная сила на шестерню, равное осевому усилию на колесе
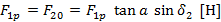 (79)
(79)
 = 20° - угол зацепления;
= 20° - угол зацепления;
 - половина угла при вершине делительного конуса колеса;
- половина угла при вершине делительного конуса колеса;
радиальное усилие на колесе равное осевому усилию на шестерне
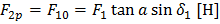 (80)
(80)