Эксперименты, поставленные аббатом Ноле и затем Пфеффером, продемонстрировали стремление раствора вобрать в себя растворитель. Количественно это выражалось высотой столба жидкости, достигнутой при состоянии равновесия на установке, схема которой приведена на рисунке 1.10. Сейчас уже мы понимаем, какие силы заставляют молекулы растворителя проникать через мембрану, преодолевая противодавление столба жидкости, - это силы гидратации ионов и молекул растворенного вещества.
Движущей силой любого переноса вещества из одного состояния в другое (в нашем случае через мембрану) является в общем виде разность химических потенциалов. Химический потенциал i-го компонента в смеси
µi = µio + RT ln ai + ViP (1.4)
где µiо – химический потенциал одного моля чистого вещества,
аi – активность,
Vi – молярный объем.
Рассмотрим устройство прибора, который называется осмометром (рис.1.15).
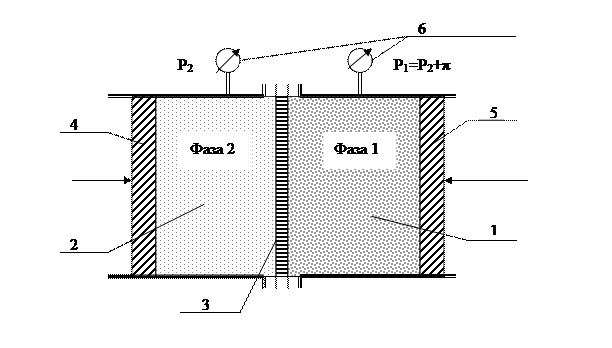
Рис. 1.15. Схема осмометра – прибора для измерения осмотического давления:
1 – камера раствора; 2 – камера растворителя; 3 – полупроницаемая
мембрана; 4,5 – поршни, 6 – манометры.
Химические потенциалы растворителя в фазе 1 и в фазе 2 при достижении равновесия равны:
µ1о + RT ln a1 + V1P1 = µ2o + RT ln a2 + V2P2 (1.5)
До тех пор, пока потенциалы не сравняются, будет происходить перенос растворителя из фазы 2 в фазу 1, а при фиксированном объеме камеры 1 в ней за счет переноса будет повышаться давление. При достижении равновесия
Р1 = Р2 + π (1.6)
где π – приращение давления за счет осмоса.
То давление, которое надо создать в растворе для предотвращения переноса в него растворителя через полупроницаемую мембрану, называется осмотическим давлением раствора.
В уравнении 1.5 µ1о = µ2о, а молярные объемы V1 ~ V2 и для чистого растворителя, и для малоконцентрированного раствора. Поэтому его можно преобразовать следующим образом:
RT (ln a2 – ln a1) = πV (1.7)
В камере 2 находится чистый растворитель, т.е. а2 = 1. В камере 1 – раствор, для которого с учетом закона Рауля (активность компонента равна его молярной доле) можно записать следующее преобразование:
ln a1 = ln y1 = ln (1-x1) = -x1 (1.8)
где у1 – молярная доля растворителя в растворе;
х1 – молярная доля растворенного вещества в растворе,
тогда выражение 1.7 можно записать:
X1
π = RT ∙ ---- (1.9)
V
N мол. pаств.в-ва А
Учтем, что х1 = ----------------------------, а размерность V - -------------------,
N мол.растворителя моль раств-ля
Тогда выражение 1.9 запишем в виде уравнения Вант-Гоффа:
N мол.раств.вещ-ва m
π = RT ∙ -------------------------- = С∙ RT = ---- ∙ RT (1.10)
V растворителя M
где С – молярная концентрация растворенного вещества в растворе;
m – массовая концентрация растворенного вещества;
М – его молекулярная масса.
Наконец, вспомним, что для растворов диссоциирующих электролитов в уравнение 1.10 добавляется поправочный коэффициент i, который практически равен числу образующихся в растворе ионов.
Таким образом, осмотическое давление является мерой степени перестройки структуры воды при внесении в нее растворяемых компонентов. Связи молекул воды с вносимыми в нее веществами по механизму и по энергетике зависят в основном от свойств вносимого вещества, но возникают они всегда.
Проведем расчет величины осмотического давления для различных веществ, возникающего при внесении их в воду.
Пример 1.1. Определить величину π водопроводной воды: солесодержание (по NaCl) –
0,5 г/л, температура – 10оС.
Молекулярная масса – 58,5; ТоК = 283; R = 8,31; i = 2.
0,5
π = 2 ∙ ----------- ∙ 8,31 ∙ 283 = 40∙103 Па = 0,4 бар.
58∙5∙10-3
Проверим размерность:
Моль дж дж н
[π] = ------ ∙ ---------- ∙ оК = ------ = --- = Па
м3 моль∙оК м3 м2
Пример 1.2. Определить величину π воды Черного моря: солесодержание (по NaCl) –
32,0 г/л; температура – 20оС.
Молекулярная масса – 58,5; R = 8,31; i =2.
32,0
π= i ∙ C ∙ RT = 2 ∙ ----------- ∙ 8,31 ∙ 293 = 2,66 ∙ 106 Па = 26,6 бар = 266 м вод.ст.
58,5∙10-3
Пример 1.3. Определить величину π раствора альбумина: масс. концентрация – 30 г/л;
Молекулярная масса – 65000; температура – 30оС; i = 1.
π= i ∙ C ∙ RT = 1 ∙ ------------ ∙ 303 ∙ 8,31 = = 1.1 ∙ 103 Па = 0,011 бар
65000∙10-3
Осмотическая машина
В принципе осмотическая машина использует явление осмоса для выработки энергии. Схема ее представлена на рисунке 1.16.

Рис. 1.16. Принципиальная схема осмотической машины
Представим, что в качестве пресной воды используется речная вода, а в качестве раствора – морская вода (впадение реки в море).
Разность осмотических давлений двух потоков (полезная разность):
Δπ = πмв - πрв (1.11)
Для того чтобы процесс переноса шел интенсивно, на стороне потока морской воды будем поддерживать рабочее давление Р ниже Δπ. При этом квадратный метр мембраны будет в единицу времени пропускать G м3/м2с воды (удельная производительность мембраны):
G = KG (Δπ – Р) (1.12)
где КG – коэффициент удельной производительности, м3/м2с Па.
Мощность, вырабатываемая при этом единицей площади мембраны, равна произведению потока на давление:
N = G ∙ P = KG (Δπ – P) ∙ P (1.13)
Пример 1.4. Рассчитать мощность, вырабатываемую 1 м2 мембраны в осмотической
машине при следующих условиях: КG = 3∙10-11 м3/м2с Па;
πмв = 2,66∙106 Па; πрв = 0,04∙106 Па; Рраб – половина разности Δπ.
Nуд = КG (Δπ – Р) ∙ Р = 3 ∙ 10-11 ∙ (2,62 – 1,31) ∙ 106 ∙ 1,31 ∙ 106 = 5,15 ∙ 10 вт = 51,5 вт.
N уд = 3∙10-11 (2,62 – 2,0) ∙ 106 ∙ 2,0 ∙ 106 = 37,2 вт.
Nуд = 3 ∙ 10-11 (2,62 – 0,62) ∙ 106 ∙ 0,62 ∙ 106 = 37,2 вт.