3.3.1 Для заполнения данной таблицы необходимо провести именную адресацию, т.е. определить имя соответствующих столбцов, для чего:
- выделить данные столбца вместе с заголовком;
- активизировать меню “Вставка”, выбрать “Имя”, “Присвоить”;
- в открывшемся окне набрать название данного столбца и зафиксировать название “ОК”;
- провести аналогичные действия с другими столбцами.
3.3.2 Рассчитать стандартизованные показатели по формуле:
Xij
 = Y (1)
= Y (1)
Xij max
где i – номер строки;
j – номер столбца;
X – значение;
Xmax – максимальное значение по данному столбцу;
Y – результат деления, показывающий долю показателя предприятия к максимальному значению показателя в отрасли.
3.3.3 Для заполнение строки “Максимальное значение” необходимо выбрать максимальное значение в столбце, выделить его щелчком левой кнопки мыши рамкой и скопировать в строку “Максимальное значение” для чего:
- щелкнуть по пиктограмме “Скопировать”;
- щелкнуть по строке “Максимальное значение” соответствующего столбца;
- щелкнуть по пиктограмме “Вставка”.
3.3.4 Чтобы создать таблицу 2 - Стандартизованные показатели, выделить заголовок таблицы 1 и скопировать его на свободное поле.
3.3.5 Создать необходимое число строк равное количеству исследуемых предприятий и заполнить значениями, для чего:
- переключить регистр с русского на английский при помощи клавиш “Ctrl + Shift”;
- выделить первую строку первого столбца (X11) левой кнопкой мыши и ввести формулу “ =(B5/B22)^2 ”, где B5 – первое значение таблицы 1; B22 – максимальное значение по данному столбцу (нажатием клавиши клавиатуры F4, В22 примет вид $B$22); знак ^ умножения берется с клавиатуры;
- нажать Enter. В строке появиться результат;
- скопировать его в другие строки данного столбца. Действовать аналогично заполнению таблицы 1;
3.3.6 Повторить действия с другими графами.
3.3.7 Для получения суммарной рейтинговой оценки ввести:
- формулу: =СУММ (B37:J37);
- скопировать формулу в остальные ячейки;
3.3.8 Для расчета рейтинговой оценки ввести: = КОРЕНЬ (K37), (через fx функцию) и скопировать результат в остальные ячейки.
3.3.9 Предыдущие два действия можно объединить в одно, для чего левой кнопкой мыши щелкнуть по пиктограмме fx функция, корень. Тогда в формульной строке появиться формула: = КОРЕНЬ ().
3.3.10 В скобки ввести: СУММ (B37:J37), (номера строк и столбцов взяты в качестве примера).
3.3.11 Подтвердить ввод щелчком мыши в первой строке столбца “Рейтинговая сумма”.
3.3.12 Скопировать результаты для всех предприятий.
3.3.13 Для простановки мест по ранжиру выполнить команду:
- выделить столбцы “Рейтинговая сумма” и “Места по ранжиру”;
- в меню “Данные”, “Сортировать”, в открывшемся окне “Сортировать по убыванию”.
3.3.14 Сделать выводы о работе.
Вопросы для защиты работы
4.1 Метод и методика АХД.
4.2 Перечислить способы обработки экономической информации.
4.3 Суть способа сравнения.
4.4 Типичные ситуации использования метода сравнения.
4.5 Суть комплексного многомерного метода сравнения в АХД.
4.6 Этапы проведения анализа.
4.7 Преимущества методики многомерного сравнительного анализа.
4.7 Преимущества расчетов с использованием электронной таблицы “Excel”
Практическая часть
| Значения коэффициентов | |||||||||
| № предприятия | рентабель -ность продаж | рентабель -ность капитала | рентабель -ность издержек производства | автономии | обеспечен-ности собствен-ными оборот-ными средствами | текущей ликвидности | абсолютной ликвидности | запас финансовой устойчи-вости | фондо-отдачи |
| 0,44 | 0,50 | 0,93 | 0,57 | 0,24 | 0,51 | 0,06 | 0,89 | 0,15 | |
| 0,60 | 0,39 | 0,64 | 0,78 | 0,47 | 0,35 | 0,8 | |||
| 0,79 | 0,32 | 0,66 | 0,75 | 0,78 | 0,73 | 0,92 | 0,60 | 0,48 | |
| 0,23 | 0,49 | 0,92 | 0,51 | 0,58 | 0,09 | 0,79 | 0,65 | ||
| 0,23 | 0,59 | 0,82 | 0,77 | 0,43 | 0,74 | 0,04 | 0,87 | 0,09 | |
| 0,53 | 0,46 | 0,59 | 0,44 | 0,92 | 0,27 | ||||
| 0,79 | 0,37 | 0,60 | 0,87 | 0,64 | 0,67 | 0,28 | 0,53 | ||
| 0,66 | 0,42 | 0,51 | 0,92 | 0,16 | 0,55 | 0,48 | 0,44 | ||
| 0,50 | 0,32 | 0,82 | 0,40 | 0,79 | 0,84 | 0,63 | 0,68 | ||
| 0,40 | 0,34 | 0,30 | 0,57 | 0,60 | |||||
| 0,86 | 0,59 | 0,24 | 0,89 | 0,76 | 0,82 | 0,92 | |||
| 0,73 | 0,44 | 0,57 | 0,53 | 0,69 | 0,82 | 0,07 | 0,95 | 0,51 | |
| 0,35 | 0,73 | 0,36 | 0,55 | 0,33 | 0,73 | 0,43 | 0,77 | 0,62 | |
| 0,34 | 0,44 | 0,70 | 0,84 | 0,20 | 0,92 | 0,59 | |||
| 0,17 | 0,56 | 0,28 | 0,80 | 0,64 | 0,57 | 0,51 | 0,48 | ||
| 0,93 | 0,27 | 0,41 | 0,47 | 0,76 | 0,08 | 0,67 | 0,65 |
| № предприятия | Значения коэффициентов | ||||||||
| рентабель -ность продаж % | рентабель -ность капитала % | рентабель -ность издержек производства % | автономии | обеспечен-ности собствен-ными оборот-ными средствами | текущей ликвидности | «000 Л ЮТ-НОЙ ликвидности | запас финансовой устойчи-вости | фондо-отдачи | |
| б | |||||||||
Тзбл.2 - Стандартизованные показатели
Таблица 3 - Рейтинговая оценка предприятия и его место по ранжиру
| № предприятия | рейтин-говая сумма | место по ранжиру |
Практическая работа № 4
Тема: Стохастический факторный анализ
Цель работы: Познакомиться с методикой проведения стохастического факторного анализа способом парной корреляции, установить стохастическую (вероятностную) зависимость между факторами, рассчитать тесноту и силу влияния связи с использованием компьютерной программы «Электронные таблицы Excel».
Теоретическая часть
Стохастическая (вероятностная) зависимость – это неполная, вероятностная связь между факторами, которая проявляется в массе наблюдений.
Различают парную и множественную корреляции.
Парная корреляция – это связь между двумя показателями, один из которых факторный, другой – результативный
Множественная корреляция – это связь, которая возникает от взаимодействия нескольких факторных показателей с результативным показателем.
Метод парной корреляции позволяет установить форму и тесноту связи между показателями. В зависимости от формы связи рассчитывают коэффициент корреляции (при линейной форме связи) или корреляционное отношение (при криволинейной форме связи).
Наиболее простой формой связи является прямолинейная зависимость между двумя показателями (парная корреляция), которая может быть описана уравнением прямой:
Yx=а+b*х (1)
где Yx - результативный показатель, который имел бы такое значение в случае детерминированного (функционального) анализа
а – параметр, показывающий высоту прямой над осью абсцисс и не имеющий экономического смысла
b – параметр, показывающий как изменится результативный показатель
х – факторный показатель
В зависимости от числового значения коэффициента корреляции различают связь:
- отсутствует, если Ккор.=0
- слабая, если Ккор.=0,1-0,5
- заметная, если Ккор.=0,5-0,7
- тесная, если Ккор.=0,7-0,9
- очень тесная, если Ккор.>0,9
- функциональная, если Ккор.=1.
Сила влияния показывает, на сколько процентов (в скольких случаях из ста) результативный показатель зависит от рассматриваемого фактора.
Разница ста процентов и силы влияния (100% - Св.) показывает влияние второстепенных факторов на результативный показатель.
Формулы для расчета
1. Среднее значение результативного показателя
 (2)
(2)
2. Среднее значение факторного показателя
 (3)
(3)
3. Среднеквадратичное отклонение результативного показателя
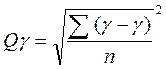 (4)
(4)
4. Среднеквадратичное отклонение факторного показателя

 (5)
(5)
5. Среднеквадратичное отклонение факторного и результативного показателей
 (6)
(6)
6. Коэффициент корреляции
Ккор. =  (7)
(7)
7. Расчет параметров уравнения прямой
Расчет параметров «а» и «в» находим из системы управлений:
 (8)
(8)
где n- число наблюдений (объектов). Значение сумм берутся из таблицы 1, приложение.
8. Сила влияния фактора на результат Св.=  (9)
(9)