Упражнение 3. Сумма, каких двух натуральных чисел равна их произведению.
ИКР: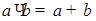 
.
Решение: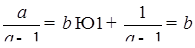 
, а значит 
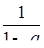целое. Но это число может быть целым только при 
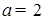. Ответ: 
.
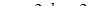Упражнение 4. Сумма, каких двух натуральных чисел больше чем их произведение.
ИКР: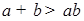 
.
Решение: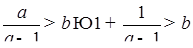 
. Т.к.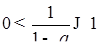 
.
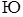
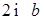Тогда если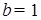 
тогда 
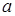любое (
).
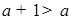Если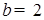 
тогда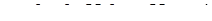 
Ответ: Только в том случаи, если одно из чисел есть 1.
Упражнение 5. По разные стороны от прямого шоссе расположены две деревни. В каком месте на шоссе нужно построить автобусную остановку, чтобы расстояние от каждой деревни до нее было одинаковым? Шириной шоссе пренебречь.
ИКР. Для решения воспользуемся принципом ИКР: соединим отрезком k (дорога) две точки A и B (две деревни). Если середина M в точности попадает на дорогу (l), то задача решена (рис. 1).
Решение. Рассмотрение случая, когда центр отрезка k не лежит на прямой l, подталкивает на мысль, что двигая прямую k, точка М помогает легко найти требуемую точку С, восстановив к ней перпендикуляр и рассмотрев равнобедренные треугольник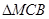и 
и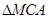 
(рис. 2).
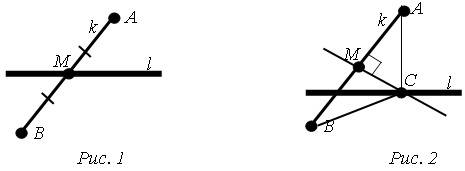
Конечно, стоит сделать вывод о том, что задача не будет иметь решения, если отрезок k будет перпендикуляром к прямой l.
Упражнение 6. Задачи для самостоятельно решения.
1. А где нужно строить автобусную остановку, если деревни расположены по одну сторону от шоссе?
2. Какое натуральное число больше его единиц в семь раз?
3. Какую последнею цифру может иметь квадрат натурального числа?
4. Какую последнею цифру может иметь куб натурального числа?
5. Найдите число, одна треть с одной четвертью которого составляет 21
6. Полтрети – число 100. Что это за число?
7. Докажите, что если произведение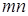 
нечетно, то и число m нечетно, и число n нечетно.
|
|
8. Докажите, что всякое нечетное число, не равное единице, есть разность квадратов двух каких-то чисел.
9. В комнате находятся 5 человек. Докажите, что найдутся 2 человека, сделавшие одинаковое число рукопожатий.
10. Сколько существует четырехзначных чисел с суммой цифр 34?
11. Петя решал пример 47+48+49+…+58 и у него получился ответ 1266. Покажите, что Петя где-то ошибся.
12. Сколько чисел от 1 до 100 ни делится, ни на 2, ни на 3?
Подведение итогов. Домашнее задание.
Занятие № 3. Метод Мозгового Штурма (ММШ)
Цель занятия: познакомить учащихся с ММШ как инструментом для активизации мышления.
Повторение: ИКР.
Игра «Муха». Рисуется таблица размером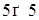 
на доске. Учащимся говорится, что в точке М находится муха, которая умеет передвигаться по шагам (вверх, вниз, влево, вправо). Задача ребят внимательно мысленно следить за движением «мухи», движение которой задает учитель.
Затем предлагается муху поместить в таблицу большим размером. И попробовать поиграть снова.
А теперь давай посмотрим на эту игру немножко с другой стороны. Нам были даны начальные условия (муха находится в точке М, перемещается по шагам) и поставлена задача (определить, где будет находиться «муха» после команд, которые будут зачитываться). Для решения этой проблемы достаточно было мысленно перемещать после каждой команды «муху», в итоге после последней команды мы получали ответ на поставленную задачу. Т.е. у нас были начальные условия, от которых мы двигались к требуемому результату, который на прошлом занятии мы формулировали как ИКР, а он в свою очередь способствовал решению наших задач.
|
|
А если поставлена какая-нибудь проблема и нам ей требуется решить. Дамы знаем начальные условия, да мы можем сформулировать ИКР, но как приблизится к решению, здесь нам не кто не говорит, куда надо двигаться, а хотелось бы.
Один из таких методов, который помогает приблизиться к решению задачи, мы сегодня разберем. Метод мозгового штурма, метод коллективного придумывания идей, который активно использовался во второй половине 20 века на многих крупных зарубежных компаний: Samsung, LG, General Motors и многие другие.
Что такое МШ?
Никому не пожелаешь побывать в переделке типа той, в которую попал американец Алекс Осборн. Представьте себе: вторая мировая война, в открытом океане караван грузовых судов. И так уж случилось, что в какой-то момент они остались без охраны. И вдруг радиотелеграмма: будьте внимательны - в вашем районе действует немецкая подводная лодка. Алекс - он был капитаном одного из этих кораблей - живо себе представил: вот показывается перископ подлодки, а вот и торпеда, оставляя за собой мелкие буруны, мчится прямо в борт. Что делать? Задача, казалось бы, неразрешимая.
И тогда капитан вспомнил практику, к которой в затруднительных положениях прибегали еще средневековые пираты. Выстроилась на палубе вся команда, и все, начиная с младших матросов, отвечали только на один вопрос: как спастись в ситуации торпедной атаки? Можно говорить все, что только придет в голову! - а вдруг чья-то «дикая» идея послужит ключиком к решению проблемы... Например, повар подал такую идею: давайте все выбежим на борт и одновременно подуем на торпеду. Глядишь, и сдуем ее с курса - мимо пройдет...
|
|
Им повезло. Подлодка не появилась. Но после войны Осборн вспомнил этот случай и однажды в компании друзей решил проанализировать ситуацию. Вспомнил и предложение повара. И спокойный анализ показал, что абсурдная идея кока привела к настоящему решению! Конечно, «мощным дувом» торпеду не повернешь, как щеки ни напрягай. Но зато ее можно немного притормозить и сбить с курса струей корабельной помпы, которая есть на каждом судне. Конечно, успех не гарантирован - но когда на карту поставлена жизнь, стоит попытаться...
Почему бы не использовать такой способ поиска новых идей в мирной жизни? В 1953 году бывший капитан Алекс Осборн выпускает книгу «Управляемое воображение». С нее-то и началась популяризация мозгового штурма в Америке, а затем и в других странах.
Наверное, вы замечали за собой, когда у вас появляется какая-нибудь, по вашему мнению, хорошая идея решения и в этот момент кто-нибудь начнет критиковать вас, то вы мгновенно «скисаете», резко снижается желание придумывать решение дальше.
С другой стороны, ряд людей не доверяют и собственным идеям. Самокритика – нормальное и здоровое свойство личности, но порой именинно она закрывает дорогу дальнейшей творческой деятельности.
Пример: о том, что звук можно искусственно передавать на расстоянии (телефон), физики задумывались еще в 60-х годах XIX века. Над проблемой работал англичанин Чарльз Уитстоун и немец Йоханн Рейс, а американский ученый впоследствии со слезами на глазах говорил, что идея множество раз приходила ему в голову, но он множество раз откидывал её как нелепую.
Учитывая все замечания, предлагается разбить весь процесс принятие решений на стадии.