Теоретические сведения
При постоянном резервировании резервные элементы 1,2,....,n соединены параллельно с основным (рабочим) элементом в течение всего периода работы системы. Все элементы соединены постоянно, перестройка схемы при отказах не происходит, отказавший элемент не отключается. Резервирование называется общим, если резервируется вся система, состоящая из последовательного соединения n элементов. Схема общего резервирования показана на рис.4.1. Основная цепь содержит n элементов. Число резервных цепей равно m, т. е. кратность резервирования равна m.
Рисунок Общее резервирование с постоянно включенным элементом
Вероятность отказа системы c общим резервированием qc(t) определяется формулой
(4.1)
где qj(t) - вероятность отказа j - го элемента.
В случае равенства вероятностей отказа основной и резервных систем
(4.2)
Вероятность безотказной работы системы
(4.3)
где Рi(t) - вероятность безотказной работы i- го элемента.
При экспоненциальном законе надежности отдельных элементов имеем
(4.4)
Определим количественные характеристики надежности системы с общим резервированием (резервные цепи включены постоянно).
Приняты следующие допущения:
Отказ элементов системы описывается простейшим потоком отказов
Резервируемые и резервные элементы равнонадежны
Известно:
Число основных элементов в системе, n
Вероятность безотказной работы элемента pi
Кратность резервирования, m
Запишем вероятность безотказной работы j - ой цепи
(4.5)
где Рij(t), j=0,1,2,...m; i=1,2,3,...,n - вероятность безотказной работы элемента j-ой цепи.
Вероятность отказа j - ой цепи
. (4.6)
Вероятность отказа системы с общим резервированием
. (4.7)
Вероятность безотказной работы системы с общим резервированием
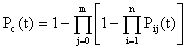. (4.8)
Частный случай: основная и резервные цепи имеют одинаковую надежность, т.е.
Рij(t)=Pi(t). (4.9)
Тогда
(4.10)
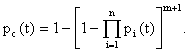(4.11)
Рассмотрим экспоненциальный закон надежности, т. е.
-. (4.12)
В этом случае формулы (4.10), (4.11) примут вид
, (4.13)
, (4.14)
, (4.15)
где Λ0 - интенсивность отказов любой из m+1 цепи, состоящей из N элементов.
Частота отказов системы с о6щим резервированием
. (4.16)
Интенсивность отказов системы с общим резервированием
. 
(4.17)
Среднее время безотказной работы резервированной системы
, (4.18)
где Т0 = 1/λ0 - среднее время безотказной работы нерезервированной системы.
Кратность резервирования
где
P(t) – ВБР элемента в течении времени t, Pc(t) – ВБР системы.
Решение типовых задач.
Задача 4.1. Система состоит из 10 равнонадежных элементов, среднее время безотказной работы элемента mt = 1000 час. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы и основная и резервная системы равнонадежны. Необходимо найти среднее время безотказной работы системы mtc, а также частоту отказов fc(t) и интенсивность отказов λс(t) в момент времени t = 50 час в следующих случаях:
а) нерезервированной системы,
б) дублированной системы при постоянно включенном резерве.
В) выигрыш по среднему времени безотказной работы
Решение.
а)
,
где λс - интенсивность отказов системы;λ i - интенсивность отказов i - го элемента; n = 10.
λi=1/mti = 1/1000=0,001; i = 1,2,...,n;
λc=0,001*10=0,01 1/час;
mtc=1/λc=100 час;
fc(t)= λc(t)* Pc(t)= λce-λct =0,01*e-0,01*50=10-3 1/час;
б) структурная схема для приведенного резервирования имеет вид
; 
час;
Используя формула 4.16 и 4.17 получим
;
.
в) выигрыш надежности по mt рассчитывается по формуле
Таким образом, использование резервирования устройства, среднее время безотказной работы увеличивается в15 раз.
Задача 4.2. В системе телеуправления применено дублирование канала управления. Интенсивность отказов канала λ=10-2 1/час. Рассчитать вероятность безотказной работы канала Рс(t) при t=10 час, среднее время безотказной работы mtc, частоту отказов fc(t), интенсивность отказов λс(t).
Решение. В данном случае число элементов n=1; λi= 10-2; кратность резервирования m=1. По формуле (4.14) имеем
Рс(10)=1-(1-e-0,1)2 =1-(1-0,9048)2 =0,99.
Определим mtс. Из формулы (4.18) имеем
Определим частоту отказов fc(t) по формуле 4.16. Получим
Определим интенсивность отказов λс(t). Имеем
Задача 4.3
Определить кратность резервирования системы с постоянно включенным резервом, обеспечивающим ВБР 0,96 в течении времени t=150ч. Элементы системы равнонадежны и имеют экспоненциальное распределение со средним временем безотказной работы Т=300ч.
Решение.
Кратность резервирования m находим по формуле
где
P(t) – ВБР элемента в течении времени t, Pc(t) – ВБР системы.
Для экспоненциального распределения P(t) находим по формуле
Подставляя значения P(t) и Pc(t) получаем
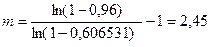
Округляя до целых чисел величину m получаем кратность резервирования равна 3.
Задача 4.4
В организации оборудован центр обработки данных в следующем составе: сервер приложений (СП), сервер данных (СД), маршрутизатор. Сервер приложений и сервер данных подключены через источник бесперебойного питания (ИБП). СП имеет следующую конфигурацию: 2-х процессорный, 2 блока питания, 1 диск, 2 сетевые карты. Сервер остается работоспособным при 1 работающем процессоре, 1 сетевой карте и 1 блоке питания. СД представляет собой сетевую систему хранения данных в составе 4 дисковых модулей. Два модуля включает 2 диска, один из них используется для организации RAID-массива. Два модуля включают по одному диску.
Определить ВБР ЦОД в течении года. Принять следующие допущения. Все элементы
одного типа равнонадежны, известны величины λi. ЦОД работает в режиме 24/7.
Решение.
ЦОД описывается как последовательно-параллельная система, для которой структурная схема резервирования имеет вид:
1-эл.сеть, 1- ИБП, 2-ЦП1, 3-ЦП2, 4-БП1, 4-БП2, 5-Диск СП, 6 – сет.карта1, 7-сет.карта2, 8-диск1 модуля 1, 8- диск2 модуля 1, 9-диск1 модуля 2, 9-диск2 модуля 2, 10- диск1 модуля 3, 11- диск1 модуля 4, 12-маршрутизатор.
Элементы 4,8,9 – работают в нагруженном резерве, элемент 1 – работает в облегченном резерве с коэффициентом kλ.
Для ППС ВБР находится по следующей формуле:
, (4.20)
где F(t) – функция распределения наработки до отказа.
(4.21),
для i=4,8,9, m4=2, m8=2,m9= 2, m2,5,6,10,11,12=1
FI(t)=1-P1(t),
, 
, Fi(t) по формуле 4.21
В таблице приведены результаты промежуточных и окончательного расчета.
| t, час | |||||||||||
| i | λ | λt | λtm | m | EXP(-λtm) | Fi | Pi | Группы | Узлы | I | Система |
| 0,00006000 | 0,5256 | 0,5256 | 0,4313 | 0,5687037198 | 0,4312962802 | 0,4312962802 | 0,4312962802 | I | |||
| 0,00004000 | 0,3504 | 0,3504 | 0,70441 | 0,2955937291 | 0,7044062709 | 0,912624347 | 0,373196543 | II | 0,999974119 | ||
| 0,00003000 | 0,2628 | 0,06906384 | 0,93327 | 0,0667329016 | 0,9332670984 | 0,9332670984 | |||||
| 0,00003500 | 0,3066 | 0,3066 | 0,73594 | 0,2640550800 | 0,7359449200 | 0,7359449200 | |||||
| 0,00000060 | 0,005256 | 0,005256 | 0,99476 | 0,0052422114 | 0,9947577886 | 0,999972519 | |||||
| 0,00002000 | 0,1752 | 0,03069504 | 0,96977 | 0,0302287306 | 0,9697712694 | 0,9697712694 | 0,079886374 | III | |||
| 0,00000020 | 0,001752 | 3,0695E-06 | 0,0000030695 | 0,9999969305 | 0,9999969305 | ||||||
| 0,00000350 | 0,03066 | 0,03066 | 0,96981 | 0,0301947492 | 0,9698052508 | 0,9698052508 | |||||
| 0,00000250 | 0,0219 | 0,0219 | 0,97834 | 0,0216619360 | 0,9783380640 | 0,9783380640 | |||||
| 0,00000023 | 0,0020148 | 0,0020148 | 0,99799 | 0,0020127717 | 0,9979872283 | 0,9979872283 | 0,0020127717 | IV |
Варианты задач для самостоятельной работы
Задача 1
Варианты 1-10.
Для резервирования методом замещения принять следующие параметры переключателя: Qп=0,04; Pп=0,96.
1. Интенсивность отказов элементов системы λ=0.0025 час-1 . Требуется определить кратность резервирования системы с постоянно включенным резервом в течении времения t=150ч., построенную из этих элементов, которая обеспечивает среднее время безотказной работы T1ср=800 ч. Принять, что элементы равнонадежны и имеют экспоненциальный закон распределения. 
2. Найти показатели надежности (ВБР) резервированной системы с постоянно включенным резервом кратности m=3, элементы которой имеют интенсивности отказов λ0=0.004 час-1, λ1=0.007 час-1, λ2=0.002 час-1 λ3=0.001 час-1. Время непрерывной работы системы t=120ч.
3. Интенсивности отказов элемента λ=0.0035 час-1. Требуется определить кратность резервирования системы (резервирование замещением) в течении времени t=250ч., построенную из этих элементов, которая обеспечивает среднее время безотказной работы T1ср=800 ч. Принять, что элементы равнонадежны и имеют экспоненциальный закон распределения. 
4. Дана последовательно-параллельная система размером 3х5 (5 элементов нерезервированной системы, 3 дублированы с резервом методом замещения). Все элементы равнонадежны и имеют интенсивность отказов элемента λ=0.002 час-1,. . Требуется определить ВБР системы. Принять, что элементы имеют экспоненциальный закон распределения. Время непрерывной работы системы t=220ч.
5. Найти показатели надежности Pc(t), Tc(t), λc(t) резервированной системы из 4-х элементов с резервирование замещением кратности m=3, элементы которой имеют интенсивности отказов λ0=0.004 час-1, λ1=0.007 час-1, λ2=0.002 час-1 λ3=0.001 час-1.. Время непрерывной работы системы t=120ч.
6. Даны две системы со скользящим резервом. Первая системы состоит из n=7 элементов, из которых m=3 резервные. Вторая система состоит из n=5 элементов с m=2 резервными. Определить выигрыш по ВБР. Элементы обеих систем имеют постоянную интенсивность отказов λ=0.001 час-1 . Время непрерывной работы системы t=120ч.
7. Дана последовательно-параллельная система размером 3х4 (4 элементов нерезервированной системы, 3 дублированные с облегченным резервом (kλ=0,5). Все элементы равнонадежны, время до отказа элементов имеет распределение Рэлея с параметром T=50час. Требуется определить ВБР системы. Время непрерывной работы системы t=150ч.
8. Дана последовательно-параллельная система размером 3х3 (3 элементов нерезервированной системы, 3 дублированные с резервом методом замещения). Все элементы равнонадежны и имеют интенсивность отказов элемента λ=0.002 час-1. Требуется определить ВБР системы. Время непрерывной работы системы t=150ч.
9. Элементы резервированной системы с постоянно включенным резервом имеют распределение Вейбулла времени работы до отказа. Найти выражение для среднего времени безотказной работы системы при кратности резервирования m=0,1,2,3,4,5. Вычислить среднее время безотказной работы при параметрах закона распределения α=2.5, θ=20.
Вариант 11-25
Резервированная система с постоянно включенным резервом (дублированием) состоит из двух подсистем (групп), имеющих различные законы распределения времени до отказа. Необходимо вычислить Pc(t), T1c, λc(t). Результаты оформить в виде таблицы и графика для t=0÷500 час с шагом 50. Исходные данные представлены в таблице 1.
В таблице используются следующие обозначения:
Exp (λ) – экспоненциальное распределение с параметром λ
R- распределение Релея с параметром λ
TN(mt; σt) – распределение усеченное нормальное с параметрами mt- σt -
W(α;θ) – распределение Вейбулла с параметрами α форма кривой-; θ- масштаб кривой
N(m;σ) – нормальное распределение с параметрами m; σ.
Таблица
| Вариант | Закон распределения | Вариант | Закон распределения | Вариант | Закон распределения |
| Exp(0,005), R(0,0002) | W(1,2;200) TN(400;180) | Exp(0,0015) TN(350;180) | |||
| Exp(0,004) N(400;120) | Exp(0,005), N(360;110) | R(0,0001) TN(390;190) | |||
| Exp(0,007) TN(400;120) | N(410;130) R(0,0006) | W(2;100) N(360;100) | |||
| W(3;500) R(0,0005) | TN(400;180 R(0,0004) | N(420;140) TN(380;200) | |||
| W(1,5;150) N(410,130) | Exp(0,001) W(1,1;160) | TN(400;215) Exp(0,002) |
Задача 2
В организации оборудован центр обработки данных в следующем составе: сервер приложений (СП), сервер данных (СД), маршрутизатор. Сервер приложений и сервер данных подключены через источник бесперебойного питания (ИБП). СП имеет следующую конфигурацию: N -х процессорный, M блока питания, 1 диск, 2 сетевые карты. Сервер приложений остается работоспособным при 1 работающем процессоре, 1 сетевой карте и 1 блоке питания. СД представляет собой сетевую систему хранения данных в составе K дисковых модулей, каждый модуль включает s - дисков, часть из них используется для организации RAID x -массива.
Определить ВБР ЦОД в течении года. Принять следующие допущения:
· все элементы
· одного типа равнонадежны,
· известны величины λi (см. пример решения)
· ЦОД работает в режиме 24/7.
Варианты задач.
| № варианта | N | M | K | S | x |