Дополнительные характеристики облигаций.

 

Доходность является важнейшим, но не единственным критерием выбора облигаций. Другим показателем привлекательности для инвесто­ра того или иного вида облигации является продолжительность срока до ее погашения. При увеличении последнего растет степень финансового риска для ее владельца. Безусловно, риск приобретения облигаций с купонными доходами значительно ниже риска, связанного с облигаци­ями, выплата процентов, по которым производится в конце срока. В свя­зи с этим существует ряд показателей, которые характеризуют в той или иной степени особенности распределения доходов в период времени от момента покупки облигации до момента погашения.

Одним из таких показателей является средний срок облигации. При ежегодных купонных выплатах средний срок выплат определяется как:

Т = h * (g (1+h):2 + 1): gh + 1 (2.30)

где h - сроки платежей по купонам в годах;

g - купонный процент.

Пример 2.5.Облигация номиналом 10000 руб. выпущена со сроком погашения через 4 года. Ежегодно по купонам выплачивается 12 % от номинала. Определить средний срок облигации

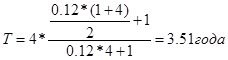
Наряда с показателей среднего срока облигации существует близ­кий ему по экономическому смыслу показатель, характеризующий сред­нюю продолжительность платежей. Иногда его называют показателем из­менчивости; обозначим его символом.

Данный показатель является средней величиной.

В случае, когда проценты по облигациям выплачиваются ежегодно, расчет средней продолжительности платежей производится по формуле;

D = S t_{j *}S_j V^t: S S_j V (2.31)

 

Пример 2.6. Облигация выпущена сроком на 4 года, номиналом 1000 руб. Ежегодно выплачиваются по купонам 12 % годовых, рыночная процентная ставка - 12,5 %. Рыночная цена облигации 985 руб.

Определить показатель продолжительности платежей.

Рассчитаем все элементы, входящие в (2.31)

t	Vt	Sj	SjVt	t SjVt
	0.8889		106.668	106.668
	0.7901		94.815	189.630
	0.7023		84.280	252.840
	0.6243	120+1000	692.973	3345.980

 

D = 3345,980: 985,0 = 3,4 года.

Приведенные формулы для расчета величин Т и Д показывают, что величина Т не зависит от рыночной процентной ставки (ссудного про­цента), в то же время величина Д зависит от ее изменения: с ростом ссудного процента его влияние на отдаленные по времени платежи пада­ет, что, в свою очередь, снижает величину Д.

Поэтому основным назначением показателя Д является определение эластичности цены по процентной ставке, т.е. измерение степени колеблемости цены облигации при незначительных изменениях величины процентной ставки на денежном рынке.

Решение этой задачи осуществляется с помощью модифицированной величины Д, которая в отечественных экономических публикациях по­лучила название модифицированной изменчивости (МД).

МД = Д/ (1+i:p) (2.32)

Где Д - средняя продолжительность платежей;

i - рыночная процентная ставка;

Р - число выплат процентов в году.

Изменение цены облигации в результате изменения процентной ставки определяется по формуле:

▲P = - 0.01*МД * ▲ i * P (2.33)

где ▲P - изменение цены облигации;

▲ i - изменение рыночной процентной ставки.

Пример 2.7. По данным примера 2.4 рассчитаем показатель моди­фицированной изменчивости

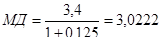
Определим, как изменится цена облигации, если рыночная процент­ная ставка возрастет с 12,5 % до 12,8 %.

▲Р= -0001*3,0222*0,3*985=-8,9306.

Откуда ожидаемое значение цены составит:

985,0 - 8,9306 = 976,0694.

Реакция цены облигации на значительные изменения рыночной про­центной ставки измеряется с помощью показателя, получившего назва­ние выпуклость (С_x).

Расчет производится по формуле

С_х= 1/(1+ i:p) * (M² +Д² + Д: Р) (2.34)

Где М² - дисперсия показателей времени платежа;

значения остальных символов те же, что и в (2.11-2.12).

М² = 1/Р S t² S_j V^t – Д² (2.35)

где Р - цена облигации.

Сдвиг в цене облигации в результате значительного изменения рыночных процентных ставок определяется как

▲P = - РМД * ▲ i: 100 +((0.5P * C_x▲ i): 10000) (2.36)

Пример 2.8. Рассмотрим возможность изменения цены облигации, если рыночная процентная ставка возросла с 12,5 % до 15,0 %, осталь­ные условия аналогичны примерам 2.4 и 2.5.

t	t2	Vt	Sj	t2 SjVt
		0.8889		106.668
		0.7901		189.630
		0.7023		252.840
		0.6243	120+1000	11187.360
Итого				12431,808

М² = 1,0611

Рассчитаем С_х:

Так как ▲i = 15- 12,5 = 2,5 %, то по (2.15) находим

▲Р= - 985,0 * 3,0222 * (15 - 12,5 / 100) + (0,5 * 985,0 * 14,2410 * 2,5²) / 1000= - 70,038

т.е. рост процентной ставки на 2,5 % вызывает снижение цены облигации до уровня 985,0 + (-70,038) = 914,962 руб.

2.6. Анализ доходности портфеля облигаций.

Набор ценных бумаг, находящихся в распоряжении инвестора, называется портфелем ценны бумаг.

Рассмотрим некоторые методы оценки портфеля облигаций. Простейший анализ портфеля облигаций заключается в оценке его полной доход­ности и среднего показателя изменчивости. Более сложный анализ свя­зан с выбором структуры портфеля, т.е. должен содержать рекомендации относительно того, какую долю капитала целесообразно вложить в тот или иной вид из циркулирующих на рынке ценных бумаг.

Годовая ставка сложных процентов, получаемых от облигаций, со­ставляющих портфельные инвестиции, может служить показателем доходности портфеля. Одним из методов определения величины этой ставки является решение уравнения, в котором общая стоимость облигаций по цене приобретения (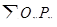) приравнивается к сумме современных величин всех платежей (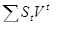). Отсюда, уравнение имеет вид:

где - количество облигаций -того вида;

- цена приобретения облигаций/'-того вида;

- платежи в момент 7^;

- дисконтный множитель по ставке i.

Средняя ставка помещения (как показатель средней доходности) может быть приближенно определена из ставок помещения каждого вида облигаций, и качестве весов можно использовать стоимость облигаций по ценам приобретения.

I = S i_jQ_jP_j : S Q_jP_j (2.37)

Существует и другой метод взвешивании. В качестве весов исполь­зуется произведение показателей изменчивости на стоимость приобрете­ния облигаций, т.е.

I = S i_j Dj QjPj: S DjQjPj (2.38)

Пример 2.9. В таблице приведены данные портфеля облигаций с со­ответствующими параметрами.

Рассчитать доходность этого портфеля облигаций.

Предварительно рассчитанные ставки помещения и показатели изменчивости облигаций данного портфеля равны:

I_a = 7,44 D_a = 6,0

I_б = 8,0 D_б= 3,5644

I_в = 10.88 D_б = 5,5163

Тогда средняя ставка помещения портфеля по (2.15) составит:

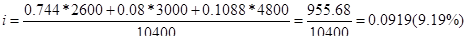
а по 2.16

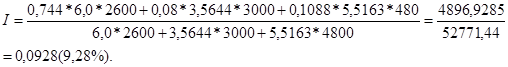
Для портфеля облигаций, как и для отдельного вида облигаций, целесообразно рассчитать показатель изменчивости, который может охарактеризовать влияние изменения рыночной процентной ставки на цену облигации, составляющих портфель.

Изменчивость портфеля облигаций определяется как средняя ве­личина: -

D= S i_j Dj QjPj: S DjQjPj (3.39)

Пример 2.10. Используя данные примера (2.9), определить по­казатель изменчивости портфеля облигаций

D = 5.0742 года

Рассмотрев методы определения доходности облигаций путем рас­чета ставки помещения, определяемой исходя из рыночной цены обли­гации, перейдем к решению обратной задачи - расчету цены облигации.

Облигации с периодической выплатой процентов без указания срока погашения.

Данный вид облигации является разновидностью веч­ной ренты, а оценку облигации в этом случае можно свести к опреде­лению современной стоимости этой ренты:

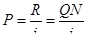
где R = QN - периодически выплачиваемый доход;

Q - процентная ставка, по которой выплачивается доход;

i - ставка помещения.

Расчетный курс такой облигации равен:

Р_к = gN/iN * 100= g/i * 100 (2.40)

При выплате дохода несколько раз в году (Р раз):

Р_к = gN/ P ((1+i)^1/p-1) * 100 (2.41)

Р_к = g/ P ((1+i)^1/p-1) * 100 (2.42)

 

Пример 2.11. Облигация без срока погашения приносит 10 % ежегодного дохода. Определить курс этой облигации, приняв ставку I помещения 12 %. Но (2.19) находим:

Р_к = 83.33

 

Если процентный доход выплачивается по полугодиям (Р = 2), то

Р_к = 85.76

 

Облигации, проценты по которым выплачиваются в момент погашения.

При погашении данного вида облигаций инвестору будет выплаче­на сумма в размере N (1+g)ⁿ Современная величина этой суммы, при дисконтировании по ставке помещения i, составит:

P = N ((1+g):(1+i))ⁿ (2.43)

Расчетный курс облигации равен

P = N ((1+g):(1+i))ⁿ (2.43)

P_n = ((1+g):(1+i))ⁿ (2.43)

Пример 2.12. По облигации номиналом 10000 руб. со сроком по­гашения 5 лет проценты в размере 8 % годовых выплачиваются в момент погашения. Ставка помещения равна 10 %. Определить расчетную цену и расчетный курс облигации

Но (2.22) определим расчетную цену:

Р = 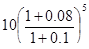= 9,1254 тыс.руб.

Расчетный курс облигации;

Р_к=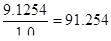

Облигации с нулевым купоном. Доход от облигаций данного ви­да образуется в результате разницы между ценой продажи и сунной, выплачиваемой владельцу облигации в момент погашения. Если пога­шение производится по номиналу, то

Р=N* V^h, а Р_к = V^h * 100. (2.45)

В случае, если цена погашения отличается от номинала, то

Р = G V^h, а Р_к= 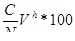(2.46)

где С - цена погашения.

Пример2.15. Коммерческий банк выпустил облигации номиналом 10000 руб. со сроком погашения через 4 года без выплаты купонных процентов. Погашение будет производиться по номиналу. Определить расчетную цену и курс облигации, если ставка помещения принята 8 % годовых.

Р = 10 • (I + 0,08)^-4 = 7,3503 тыс. руб.

Р^ = I.08^-4 • 100 = 73,5.

Изменим условия: облигации погашаются по цене 11000 руб., тогда по (2.24 а):

Р = 11 • 1,^08-4 = 8,0853 тыс. руб.

Р_к = 11 /10* 0,73503 = 80.8553

Облигации с периодической выплатой процентов и погашением в один срок. Данный вид облигации является наиболее распространен­ным. Первоначально рассмотрим облигации, по которым ежегодно вы­плачиваются проценты, а погашение производится по номиналу. В подобном случае цена и курс облигации рассчитываются следующим образом:

P = NV + R * a_h/i (2.47)

P_k = (V^t + R: N * a_h/i)* 100 (2.47а)

где R - ежегодный процентный доход;

N - номинал облигации;

n- срок от момента выпуска до погашения;

V- дисконтный множитель, рассчитанный по ставке, учитывае­мой при оценке;

a_n.i - коэффициент приведения ренты.

При выплате процентного дохода Р раз в году

P = (NV^t + R: N * a_h/i^p) (2.48)

P_k = (V^t + R: N * a_h/i^p)* 100 (2.48а)

Пример 2.14 Облигации со сроком погашения через 10 лет и ежегодным доходом 9 % погашаются по номиналу 5000 руб. Произвести оценку и определить курс облигации, если ставка процентов, приня­тая при оценке, равна 10,5 %.

Расчетные параметры:

N= 5.0; R = 5*0.09 = 0.45 V¹⁰ = (1 + 0.105)^-10=0.3684

A_10;10,5 =6,0148

Р=5,0*0,3684+0,45*6,0148=4,5487

или по (2.26а)

Р_к = (0,3684 + 0,45/5,0 • 6,0148) • 100 = 90.97.

Если бы процентный доход выплачивался дважды в год, то

а_10;10,5=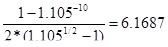

Р = 5,0 • 0,3684 + 0.45 • 6.1687 = 4,6179 тыс.руб.

Р_к =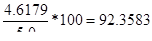

или

Р_к = (0,3684 + 0,45/5,0 * 6,1687) * 100 = 92.358 = 92,56.

Расчетная цена и курс облигаций при выплате процентов Р раз в году к цена погашения, превышающей номинал облигации, вычи­сляются по формулам:

P = (CV^t + R* a_h/i^p) (2.49)

P_c = (V^t + R: N * a_h/i^p)* 100 (2.49а)

Пример 2.15 Облигация номиналом 5000 руб. со сроком погаше­ния через 5 лет и годовым доходом 10 %, выплачиваемым дважды в год, будет выпускаться по цене 5,5 тыс. руб. Определить расчетную цену облигации, приняв ставку помещения в 12 %.

Расчетные параметры:

N=5.0 n=5 g=10% P=2 i=12% C=5.5 R=5*0,1=0,5

(a_5;12)²= 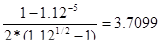V⁵= 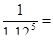0,5674

Глава 3.