При экономической оценке инвестиционных проектов используется ряд методов. Данный метод является одним из основных.
Суть метода сводится к расчету чистой текущей стоимости – NPV (net present valui), которую можно определить следующим образом: текущая стоимость денежных притоков за вычетом текущей стоимости денежных потоков, т.е. данный метод предусматривает дисконтирование денежных потоков с целью определения эффективности инвестиций.
Поскольку приток денежных средств распределен во времени, его
дисконтирование производится по процентной ставке i. Важным моментом является выбор уровня процентной ставки, по которой производится дисконтирование. В экономической литературе иногда ее называют ставкой сравнения, т.к. оценка эффективности часто производится именно при сравнении вариантов капиталовложений. Иногда коэффициент дисконтирования по выбранной ставке - i называют барьерным коэффициентом. Несмотря на различие названий, эта ставка должна отражать ожидаемый усредненный уровень ссудного процента на финансовом рынке. Важным моментом при определении процентной ставки, используемой для дисконтирования, является учет риска. Риск в инвестиционном процессе, независимо от его конкретных форм, в конечном счете предстает в виде возможного уменьшения реальной отдачи от вложенного капитала по сравнению с ожидаемой. Так как это уменьшение проявляется во времени, то в качестве общей рекомендации по учету возможных потерь от сокращения отдачи предлагается вводить поправку к уровню процентной ставки.
Она должна характеризовать доходность по безрисковым вложениям (например, краткосрочным государственным ценным бумагам), т.е. добавлять некоторую рисковей премию, учитывающую как специфический риск, связанный с неопределенностью получения дохода от конкретного капиталовложения, так и рыночный риск, связанный с конъюнктурой.
При разовой инвестиции математически расчет чистого приведенного дохода (эффекта) можно представить формулой:
N  - IC (3.1)
- IC (3.1)
где Р1, Р2, Pк, Рт - годовые денежные поступления в течение n- лет;
IC - стартовые инвестиции;
I - ставка сравнения;
 - общая накопленная величина дисконтированных поступлений.
- общая накопленная величина дисконтированных поступлений.
Очевидно, что NPV > 0 проект следует принять, NPV < 0 - проект должен быть отвергнут, NPV = 0 - проект не прибылен, но и не убыточен.
При прогнозировании доходов по годам необходимо учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Так, если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.
Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение нескольких лет (m -лет), то формула для расчета NPV модифицируется следующим образом:
 (3.2)
(3.2)
Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала фирмы в случае принятия рассматриваемого проекта. Этот показатель аддитивен во временном аспекте, т.е. NPV различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
Рассмотрим пример с использованием данного метода для оценки проекта.
Пример 3.3.Фирма рассматривает целесообразность приобретения новой технологической линии по цене 18000 у.д.е. По прогнозам сразу же после пуска линии ежегодные поступления после вычета налогов составят 5700 у.д.е. Работа линии рассчитана на пять лет. Ликвидационная стоимость линии равна затратам на ее демонтаж. Необходимая норма прибыли составляет 12 %. Следовательно, чистая текущая стоимость проекта равна по (3.I):
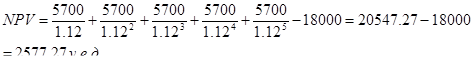
  Члены приведенного потока Члены приведенного потока
| Годы | |||||
      - 18000 - 18000
|  
|  
|  
|  
|  
| |
 5089,29 5089,29
| ||||||
 1544,00 1544,00
| ||||||
 40,57,15 40,57,15
| ||||||
 3622,50 3622,50
| ||||||
 3234,33 3234,33
| ||||||
| 20547,27 – 18000 = | ||||||
| 2547,27 |
Таким образом, эта задача решается с использованием формулы приведенной величины обычной ренты.
Общая накопленная величина дисконтированных доходов (поступлений) 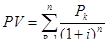 равна приведенной величине обыкновенной ренты
равна приведенной величине обыкновенной ренты

Отсюда:
A = 2700* 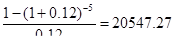 т.к. величина чистой текущей стоимости 20547.27 - 18000 = 2547.27 > 0. то проект может быть принят.
т.к. величина чистой текущей стоимости 20547.27 - 18000 = 2547.27 > 0. то проект может быть принят.
Рассмотрим пример, когда инвестиции приведены одномоментно, а годовые поступления не равны между собой.
Пример 3.4.Фирма рассматривает инвестиционный проект - приобретение новой технологической линии. Стоимость линии 15 млн. у.д.е. Срок эксплуатации пять лет. износ на оборудование исчисляется по методу прямолинейной амортизации, т.е. 20 % годовых; суммы, вырученные от ликвидации оборудования в конце срока эксплуатации, покроют расходы по его демонтажу, выручка от реализации продукции прогнозируется по годам в следующих объемах (тыс.у.д.е.):
10200; 11000; 12300; 12000; 9000.
Текущие расходы по годам оцениваются следующим образом:
5100 тыс.у.д.е. в первый год эксплуатации. Ежегодно эксплуатационные расходы увеличиваются на 4 %. Ставка налога на прибыль составляет 46 %. "Цена" авансированного капитала 14 %. Стартовые инвестиции производятся без участия внешних источников финансирования, т.е. за счет собственных средств.
Рассчитаем исходные данные по годам:
Таблица 3.3.
| Показатели | Г о | д ы | |||
| 1-й | 2-й | 5-й | 4-й | 5-й | |
| 1.Объем реализации | |||||
| 2. Текущие расходы | -5100.0 | -5304.0 | -5516.2 | -5736,8 | -5966,3 |
| 3. Износ | -5000,0 | -3000,0 | -3000,0 | -3000,0 | -3000,0 |
| 4.Налогооблагаемая прибыль | 2100,0 | 2796,0 | 3783,8 | 3263,2 | 33.7 |
| 5. Налог на прибыль | -840,0 | -1118.4 | -1513,2 | -1305.3 | -13.5 |
| 6. Чистая прибыль | 1260,0 | 1667,6 | 2270,6 | 1957,9 | 20,2 |
| 7. Чистые денежные поступления(п. 5 + п.6) | 4260,0 | 4667,6 | 5270,6 | 4957,9 | 3020.2 |
NPV = 4260 * 1.14-1 + 4667.6 * 1.14-2 +5270,6 * 1,14-3 + 4957.9 * 1.14-4 + 3020.2 * 1.14-5-15000 = 390,0 тыс..у.д.е.
Так как NPV= 390,0 тыс..у.д.е. > 0, то проект не является убыточным.
Pассмотрим другой пример, когда инвестиция распределенывовремени, доходи начинают поступать после окончания инвестиционного проекта, т.е. члены денежного потока имеют как отрицательное, так и положительное значение.
Пример 3.5. Имеются два инвестиционных проекта, в которых поток платежей на конец года характеризуется следующими данными (млн.д.у.е.):
| Годы | ||||||||
| Проект А | -200 | -300 | +100 | - | ||||
| Проект Б | -400 | -100 |
Ставка сравнения (норматив рентабельности) принята в размере 10 %.
NPVА = (-200) * 1.1-1 + (-300) * 1.1-2 + (100) * 1,1-3 + (300) * 1.1-4 + (400) * 1.1-5 + 400* 1,1-6 + 350 * 1,1-7= -429,75 + 933,8 = 504,05 тыс..у.д.е.
NPVА = (-400) * 1.1-1 + (-100) * 1.1-2 + (100) * 1,1-3 + (200) * 1.1-4 + (200) * 1.1-5 + 400* 1,1-6 + 400 * 1,1-7+ 350 * 1,1-8= -446,28 + 930,97 = 483,97 тыс..у.д.е.
В рассматриваемых примерах капиталовложения (инвестиции) и отдача от них были представлены потоками платежей, в которых отсутствовала закономерность изменений во времени. Возвратимся теперь к рассмотрению случаев, когда инвестиции и отдача от них являются потоками платежей, представляющих определенные, изменяющиеся во времени закономерности. В этих случаях расчет можно произвести, используя формулы приведенных величин рент. Если вложения и поступления равномерные и дискретные, причем доходы начинают постапать сразу же после завершения вложений, то величина NPV находится как разность современных величин двух рент.
NPV = Pk * an2/i Vhi - ICfn1/i (3.3)
где Рк_ - доходы в периоды I, 2,... n2;
С I - инвестиционные расходы в периоде 1, 2,…n1;
Vh1- коэффициент дисконтирования по ставке приведения -i;
n1 - продолжительность периода инвестиций;
n2 - продолжительность получения отдачи (дохода) от инвестиций.
Пример 3.6. Инвестиции производится поквартально по 0,5 млн. у.д.е. на протяжении трех лет (n1 = 3 года; С I = 0,5 • 4 = 2,0 млн.у.д.е. в год; Р1 = 4). Доходы начинают поступать сразу же после завершения вложений. Ожидаемая отдача оценена в размере 1,3 млн.у.д.е. в год. Поступления ежемесячные в течение восьми лет, т.е. параметры второй ренты: С I = 1,3; n2 = 8; Р2 = 12. Норматив рентабельности 10 %.


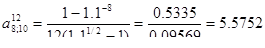

NPV = 1.3 * 5.5752 * 0.7513 – 0.5 * 4 * 2.5784 = 5.4452 – 5.1568 = 0.2884 млн.у.д.е.
Графически этот период изображен на рис. 3.1.



 Период отдачи
Период отдачи

0 1 2 3 4 5 6 7 8 9 10 11

период инвестиций
Рис. 3.1.
Период oт начала инвестиций до конца срока поступления доходов 11 лет (3 + 8). Величина А = Р * а128;10 показывает, какая сумма доходов должна быть после окончания инвестиций, т.е. после третьего года. Эта сумма обеспечивает наращение к концу срока получения доходов - А (I + i)n = S. Чтобы устранить влияние фактора времени (трех лет), ее необходимо дисконтировать с использованием множителем V3. Иначе говоря, из современной величины отсроченной ренты (дохода) вычитается современная величина немедленной ренты. Если же отдача (доходы) от инвестиций будут получены не сразу после их окончания, а например, через год, то чистый приведенным эффект (доход) будет значительно ниже.
 *
*  =
=
= 1.3 * 5.5752 * 0.6830 – 2 * 2.5784 =4,9503 – 5.1568 = -0,2065 млн.у.д.е.
Как видим, отсрочка в получении доходов на один год делает проект убыточный.
Рассмотренный варианты оценки инвестиционных проектов являются, но более чек частными случаями, которые можно встретить на практике. Зачастую инвестиционные вложения и отдача от них могут следовать различным закономерностям. Так, вложения по условиям финансирования могут носить периодический характер, в то же время отдача может быть непрерывной, благодаря отлаженному производству. Другой случай, когда поток платежей в различные периоды носит неоднозначный характер, т.е. в период освоения будет иметь одну величину, а в период выхода оборудования на полную мощность - другую и т.д.
Абсолютная величина чистого приведенного дохода зависит от двух видов параметров. Первые характеризуют инвестиционный процесс объективно. Они определяются производственным процессом (больше продукции - больше выручки; меньше затраты - больше прибыли и т.д.). Ко второму виду относится единственный параметр - ставка сравнения. Напомним, что величина этой ставки - результат выбора, результат субъективного суждения, т.е. величина условная, в силу чего целесообразно при анализе инвестиционных проектов определять NPV не для одной ставки, а для некоторого диапазона ставок.
Наши предыдущие рассуждения основывались на том, что величину NPV мы находили на начало реализации инвестиционного проекта. Однако имеется возможность определения этой величины на момент завершения процесса вложений или на иной момент времени. В этом случае чистый приведенный доход на момент t - определяется как
NPVt= NPVo (1+i)t,
где NPVo; NPVt - величины чистого приведенного дохода, рассчитанные на начало инвестиционного процесса и некоторый момент времени t после него.
Рассматривая свойства чистого приведенного дохода, необходимо обратить внимание еще на одну проблему. Дело в том, что при высоком уровне ставки отдаленные платежи оказывают малое влияние на величину NPV. В силу этого различные по продолжительности периодов отдачи варианты могут оказаться практически равноценными по конечному экономическому эффекту.