С каждой задачей линейного программирования можно связать по определенному правилу другую задачу линейного программирования, которая называется двойственной. При этом исходную задачу называют прямой. Рассмотрение двойственной пары задач линейного программирования дает полезную дополнительную информацию о свойствах оптимального плана. Опишем способы построения двойственных задач и основные результаты теории двойственности.
1. Задача оптимального планирования производства.
Как известно, эта задача формализуется как стандартная задача линейного программирования:
|






Напомним содержательный смысл параметров и переменных задачи: bi – общее количество ресурса Ri, aij – количество ресурса Ri, расходуемого на производство единицы продукта Pj, cj – прибыль от реализации единицы продукта Pj, xj – количество продукта Pj, планируемое к выпуску.
Прямая задача: найти план выпуска продукции, обеспечивающий максимальную прибыль при заданных ограничениях на расход ресурсов.
Для формулировки двойственной задачи будем учитывать ценность ресурсов. Предположим, что в рамках некоторого объединения предприятие реализует ресурсы другому предприятию. Первое предприятие оценивает свои ресурсы с точки зрения возможной прибыли от производимой продукции и условием продажи считает оценку ресурсов не меньшую, чем прибыль от готовой продукции. Второе предприятие имеет цель минимизировать стоимость приобретаемых ресурсов.
В этой связи возникает двойственная задача: установить такие цены на ресурсы (внутри объединения), чтобы минимизировать их общую стоимость (интерес покупателя) при условии, чтобы стоимость расхода ресурсов на единицу продукта была не ниже соответствующей прибыли от реализации (интерес продавца).
Проведем формализацию этой задачи. Пусть уi≥ 0, - планируемая цена (оценка) ресурса Ri, i= 1,…,m. Тогда общая стоимость ресурсов выражается величиной  .
.
Стоимость ресурсов, необходимых для производства единицы продукта Pj, равна  .
.
С учетом заявленных требований приходим к следующей задаче линейного программирования относительно переменных у1…..уm:

|


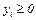


Это двойственная задача по отношению к прямой задаче (2.14). По существу, она является канонической задачей линейного программирования (как и прямая задача).
Двойственная задача - это вспомогательная задача линейного программирования, которая формулируется из исходной (прямой) задачи с помощью определенных правил.
Переменные прямой задачи.
|
| Правые части ограничения двойственной задачи | с1 | с2…… | сj | ……cn | |||
  Коэф. левых частей ограничений двойственной задачи Коэф. левых частей ограничений двойственной задачи
| а11 | а12……. | a1n | …..a1m | b1 | ←y1 | Переменные двойственной задачи |
| a21 | a22……. | a2j | …..a2m | b2 | ←y2 | ||
| : | : | : | : | : | : | ||
| am1 | am2……. | amj | …..amn | bm | ←ym |

|

|
Правила постановки двойственной задачи:
1) Каждому ограничению прямой задачи соответствует переменная двойственной задачи.
2) Каждой переменной прямой задачи соответствует ограничение двойственной задачи.
3) Коэффициенты аij при некоторой переменной - xj фигурирующие в ограничениях прямой задачи, становится коэффициентами левой части соответствующего ограничения двойственной задачи, а соответствующий коэффициент cj в целевой функции прямой при той же переменной xj становится постоянной правой части ограничений двойственной задачи.
Из правил следует, что двойственная задача имеет m переменных (у1,...,ym) и n ограничений, соответствующих n переменным прямой задачи.
Рассмотрим, как формируются направление оптимизации, ограничения и знаки двойственных переменных.
Таблица 42
| Прямая задача в канонической форме. Целевая функция fo | Двойственная задача | ||
| Целевая функция W | Знаки ограничений | Переменные | |
| максимизации | минимум | ≥ | Не ограничены в знаке |
| минимизации | максимум | ≤ | Не ограничены в знаке |